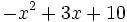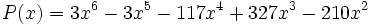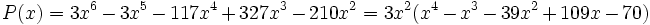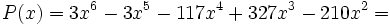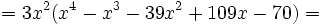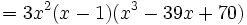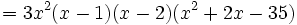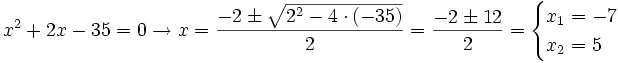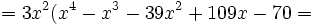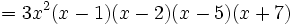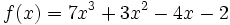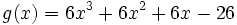Factorización de polinomios (4ºESO Académicas)
De Wikipedia
| Revisión de 18:25 15 sep 2018 Coordinador (Discusión | contribuciones) (→Raíces enteras de un polinomio) ← Ir a diferencia anterior |
Revisión de 18:26 15 sep 2018 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Raíces de un polinomio== | ||
| - | {{Raíces de un polinomio}} | ||
| - | {{p}} | ||
| - | |||
| - | ==Raíces enteras de un polinomio== | ||
| - | Tenemos un polinomio <math>P(x)\,\!</math> con raíces entera y queremos encontrarlas. Para hacerlo tenemos que ir probando a dividirlo por <math>(x-a)\,\!</math>, pero ¿qué valor puede tomar <math>a\,\!</math>? El siguiente resultado nos da la respuesta: | ||
| - | |||
| - | {{teorema: raíces enteras de un polinomio}} | ||
| - | |||
| - | ===Ejercicios propuestos=== | ||
| - | {{ejercicio | ||
| - | |titulo=Ejercicios propuestos: ''Raíces de un polinomio'' | ||
| - | |cuerpo= | ||
| - | |||
| - | (Pág. 41) | ||
| - | |||
| - | [[Imagen:red_star.png|12px]] 1 al 9 | ||
| - | |||
| - | }} | ||
| - | |||
| ==Factorización de polinomios== | ==Factorización de polinomios== | ||
| {{Caja_Amarilla|texto='''Factorizar''' un polinomio es descomponerlo en producto de polinomios con el menor grado posible.}} | {{Caja_Amarilla|texto='''Factorizar''' un polinomio es descomponerlo en producto de polinomios con el menor grado posible.}} | ||
Revisión de 18:26 15 sep 2018
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Calculadora |
Tabla de contenidos |
Factorización de polinomios
Factorizar un polinomio es descomponerlo en producto de polinomios con el menor grado posible.
Factorización de polinomios de grado 2
Factorización de polinomios de segundo grado
Un polinomio de segundo grado,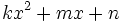 
, con raíces rales, 
y 
, se puede factorizar de la forma
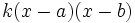
Ejemplos: Factorización de polinomios de segundo grado y reducibles
Factoriza los siguientes polinomios
- a)
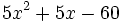
- b)
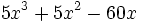
- El polinomio 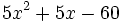tiene dos raíces:
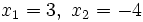, que se obtienen de resolver la ecuación de segundo grado 
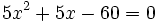. Entonces:
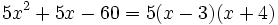
- El polinomio incompleto de grado 3, 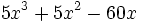, se puede descomponer de la siguiente manera:
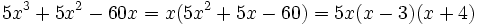
- (Observa que primero hemos sacado factor común
y luiego hemos factorizado el polinomio de grado 2, como hicimos en el ejemplo anterior).
Tutorial (8'02") Sinopsis: Descomposición factorial de polinomios de grado 2 resolviendo la ecuación de segundo grado.
Ejercicio 1 (13'56") Sinopsis: Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- 5a)
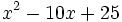
- 5b)
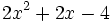
Ejercicio 2 (8'51") Sinopsis: Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- 5c)
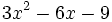
- 5d)
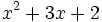
Ejercicio 3 (9'38") Sinopsis: Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- 5e)
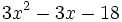
- 5f)
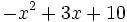
Ejercicio 4 (6'08") Sinopsis: Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- a)
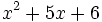
- b)
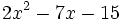
- c)
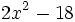
- d)
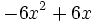
Procedimientos para la factorización de polinomios de grado mayor que 2
Procedimiento para factorizar polinomios
- Siempre que se pueda, sacaremos factor común.
- Mediante la regla de Ruffini podremos buscar las raíces enteras o fraccionarias del polinomio y obtener la factorización.
Un polinomio de grado mayor que 2 no pueda factorizarse usando los procedimientos anteriores, es poco probable que podamos hacerlo con los conocimientos que tenemos.
Factorización de un polinomio mediante la regla de Ruffini
Factorización de un polinomio por Ruffini
Para factorizar un polinomio mediante la regla de Ruffini, aplicaremos ésta sucesivamente, utilizando como candidatos a raíces enteras, los divisores del término independiente y como candidatos a raices fraccionarias, las que resultan de dividir los divisores del término independiente entre los divisores del término de mayor grado.
Cuando al aplicar la regla de Ruffini nos quede un polinomio de segundo grado en el cociente, en vez de seguir probando por Ruffini, es preferible aplicar la fórmula de la ecuación de segundo grado para obtener las dos últimas raíces y por tanto los dos últimos factores. Esto será así, siempre y cuando, el discriminante de la ecuación no sea negativo, ya que de serlo, no habrá más raíces y no podremos descomponerlo más.
Ejemplo: Regla de Ruffini
Factoriza el siguiente polinomio:
Primero sacamos factor común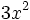 
:
Ahora aplicamos Ruffini. Los divisores de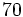 
son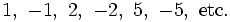 
Empezaremos probando con el 1:
| 1 -1 -39 109 -70
|
1| 1 0 -39 70
--|----------------------
| 1 0 -39 70 |0
|____
Como el resto es cero, hemos encontrado una de las raíces,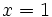 
y uno de los factores 
.
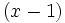Seguimos aplicando Ruffini. Probamos con 1, de nuevo ya que podría repetirse dicha raíz:
| 1 0 -39 70
|
1| 1 1 38
--|-----------------
| 1 1 38 |108
|____
El resto es diferente de cero con lo que tenemos que seguir probando, con el -1:
| 1 0 -39 70
|
-1| -1 1 38
--|-----------------
| 1 -1 -38 |108
|____
El resto vuelve a ser diferente de cero, probamos con 2:
| 1 0 -39 70
|
2| 2 4 -70
--|----------------
| 1 2 -35 |0
|____
Ya hemos encontrado otra raíz, 
, y el factor correspondiente,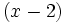 
.
El polinomio quedará de la siguiente forma:
Finalmente para encontrar las dos últimas raíces utilizamos la fórmula de la ecuación de 2º grado:
Así, sus raíces son 5 y -7 y sus factores (x-5) y (x+7).
De esta manera:
Tutorial 1 (26'17") Sinopsis:Método que nos permite factorizar polinomios de grado mayor que dos.
Tutorial 2 (9´55") Sinopsis: - Factorizar un polinomio P(x) es expresarlo como producto de otros de menor grado que él, y para ello hay que calcular los "ceros" de P(x), cosa no siempre fácil.
- Si "a" es un "cero" de P(x) y C(x) es el cociente de la división P(x)/(x-a), entonces P(x) = (x-a).C(x).
- Teorema de la factorización: si los coeficientes de un polinomio P(x) son números enteros, los ceros enteros de P(x) son divisores del término independiente de P(x).
- Si la suma de los coeficientes de P(x) es 0, pues apostar tranquilamente la vida a que el número 1 es un "cero" de P(x); o sea, P(x) es divisible por (x-1).
Tutorial 3 (9'19") Sinopsis: Cómo hacer una descomposición factorial de polinomios por Ruffini.
Ejercicio 1 (11´14") Sinopsis: Factoriza los polinomios:
- a)
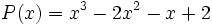
- b)
Ejercicio 2 (9´29") Sinopsis: Factoriza el polinomio 
Ejercicio 3 (9´36") Sinopsis: Factoriza el polinomio 
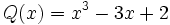
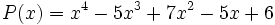
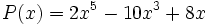
Ejercicio 4 (9´27") Sinopsis: Factoriza el polinomio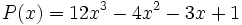 
sabiendo que sólo tiene raíces fraccionarias.
Ejercicio 5 (8'59") Sinopsis: Hallar los puntos de intersección de las dos funciones polinómicas siguientes:
Ejercicio 6 (9'25") Sinopsis: Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8a)
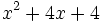
- 8b)
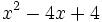
Ejercicio 7 (8'14") Sinopsis: Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8c)
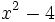
- 8d)
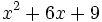
Ejercicio 8 (7'01") Sinopsis: Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8e)
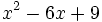
- 8f)
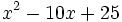
Ejercicio 9 (8'01") Sinopsis: Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8g)
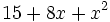
- 8h)
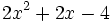
Ejercicio 10 (8'01") Sinopsis: Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8i)
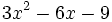
- 8j)
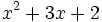
Ejercicio 11 (8'33") Sinopsis: Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8k)
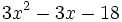
- 8l)
