Plantilla:Teorema: raíces enteras de un polinomio

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión actual

Teorema

Las raíces enteras de un polinomio con coeficientes enteros son divisores de su término independiente.

Demostración:

Demostración:

En efecto, sea $x=a\;$ una raíz entera de un polinomio con coeficientes enteros

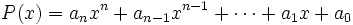
$P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$

Entonces, como 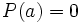$P(a)=0\;$ , tendremos que

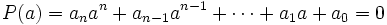
$P(a)=a_na^n+a_{n-1}a^{n-1}+\cdots+a_1a+a_0=0$

de donde, despejando el termino independiente

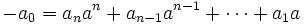
$-a_0=a_na^n+a_{n-1}a^{n-1}+\cdots+a_1a$

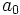Como el miembro de la derecha contiene al factor $a\;$ en todos sus sumandos, es un múltiplo de $a\;$ , entonces $a_0\;$ también. Luego $a\;$ divide al término independiente.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Teorema:_ra%C3%ADces_enteras_de_un_polinomio"

 {{teorema|titulo=Teorema
-|enunciado=:Las raíces enteras de un polinomio son divisores de su término independiente.
+|enunciado=Las raíces enteras de un polinomio con coeficientes enteros son divisores de su término independiente.
 |demo=
-En efecto, sea <math>x=a\;</math> una raíz entera de un polinomio
+'''Demostración:'''
+En efecto, sea <math>x=a\;</math> una raíz entera de un polinomio con coeficientes enteros
 <center><math>P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0</math></center>

Plantilla:Teorema: raíces enteras de un polinomio

De Wikipedia

Revisión actual

Vistas

Herramientas personales

Menú

Buscar

Herramientas