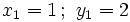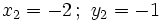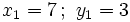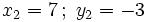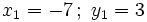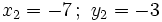Plantilla:Resolución de sistemas no lineales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:28 2 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | Para resolver sistemas no lineales también podemos usar los métodos algebraicos de sustitución, igualación y reducción. | + | Para resolver sistemas no lineales también podemos usar lo que sabemos sobre resolución de ecuaciones no lineales junto con los métodos de resolución de sistemas lineales conocidos (sustitución, igualación y reducción). |
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejercicios resueltos: | {{Ejemplo|titulo=Ejercicios resueltos: | ||
| Línea 23: | Línea 23: | ||
| :<math>x_2=-7 \, ; \ y_2=-3</math> | :<math>x_2=-7 \, ; \ y_2=-3</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicios | ||
| + | |duracion=6'59" | ||
| + | |sinopsis=Cuatro sistemas no lineales de ecuaciones. | ||
| + | |url1=https://www.youtube.com/watch?v=wTWxjkynoDg&list=PL773F27163628CA1F&index=36 | ||
| }} | }} | ||
Revisión actual
Para resolver sistemas no lineales también podemos usar lo que sabemos sobre resolución de ecuaciones no lineales junto con los métodos de resolución de sistemas lineales conocidos (sustitución, igualación y reducción).
Ejercicios resueltos:
Resuelve los siguientes sistemas:
- 1.
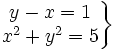
- 2.
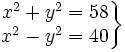
Solución:
Soluciones:
1. Tiene dos soluciones:
2. Tiene cuatro soluciones:
Cuatro sistemas no lineales de ecuaciones.