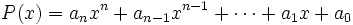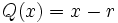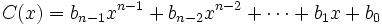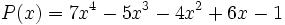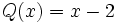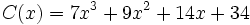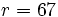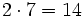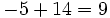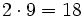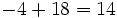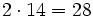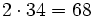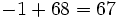Regla de Ruffini (4ºESO Académicas)
De Wikipedia
| Revisión de 16:18 14 ene 2009 Coordinador (Discusión | contribuciones) (→División de un polinomio por (x-a). Regla de Ruffini) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| __TOC__ | __TOC__ | ||
| - | ==Cociente de monomios== | + | ==Regla de Ruffini== |
| - | {{Caja_Amarilla|texto=Entenderemos la '''división de monomios''' como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base. | + | ===División de un polinomio por (x-a)=== |
| - | <center> | + | {{Regla de Ruffini}} |
| - | {{Caja|contenido= | + | |
| - | <math> \frac{ax^m} {bx^n}= \frac{a} {b} x^{m-n} </math>}} | + | |
| - | </center> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Ejemplo | + | ===División de un polinomio por (mx+n)=== |
| - | |titulo=Ejemplos: ''Cociente de monomios'' | + | {{Division de un polinomio por mx mas n}} |
| - | |enunciado= | + | |
| - | :Calcula: | + | |
| - | :a) <math>4ax^4y^3 : 2x^2y \;\!</math> | + | |
| - | :b) <math>6x^4y : 2ax^3 \;\!</math> | + | |
| - | |sol= | + | |
| - | :a) <math>4ax^4y^3 : 2x^2y = \cfrac {4ax^4y^3}{2x^2y}=2ax^2y^2</math> | + | |
| - | :b) <math>6x^4y : 2ax^3 =\cfrac {6x^4y}{2ax^3}=\cfrac {3xy}{a}</math> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | ===Ejercicios propuestos=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Regla de Ruffini'' | ||
| + | |cuerpo= | ||
| - | ==División de polinomios== | + | (Pág. 38) |
| - | La división polinómica es, en ciertos aspectos, similar a la [[Números naturales: Operaciones#División con naturales|división numérica]]. | + | |
| - | {{p}} | + | |
| - | {{Caja_Amarilla|texto=Dados dos polinomios <math>P(x)\;</math> (dividendo) y <math>Q(x)\;</math> (divisor) de modo que el grado de <math>P(x)\;</math> sea mayor o igual que el grado de <math>Q(x)\;</math> y el grado de <math>Q(x)\;</math> sea mayor o igual a cero, siempre podremos hallar dos polinomios <math>C(x)\;</math> (cociente) y <math>R(x)\;</math> (resto) tales que: | + | |
| - | <center><math> P(x) = Q(x) \cdot C(x)+ R(x) \,</math></center> | + | [[Imagen:red_star.png|12px]] 1a,e; 2a,b |
| - | <center>dividendo = divisor × cociente + resto</center> | + | |
| - | que también podemos representar como: | + | [[Imagen:yellow_star.png|12px]] 1b,c,d,f; 2c,d,e |
| - | <center><math>\begin{matrix} | ||
| - | P(x) \ | \ Q(x) | ||
| - | \\ | ||
| - | \qquad \quad |--- \, | ||
| - | \\ | ||
| - | R(x) \quad C(x) | ||
| - | \end{matrix}</math></center> | ||
| - | |||
| - | |||
| - | *El grado de C(x) está determinado por la diferencia entre los grados de P(x) y Q(x), mientras que el grado de R(x) será, como máximo, un grado menor que Q(x). | ||
| - | *Cuando el resto sea igual a cero diremos que el dividendo es '''divisible''' por el divisor, es decir, que la división es exacta. | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''División de polinomios'' | ||
| - | |enunciado= | ||
| - | Divide los siguientes polinomios: | ||
| - | :: <math> P(x) = 3 \, x^{4} - 2 \, x^{3} + 4 \, x^{2} + 2 \, \, x - 3\;</math> | + | ==Teorema del resto== |
| - | :: <math> Q(x) = x^{2} - 2 \, x - 1 \;</math> | + | {{Teorema del resto}} |
| - | |sol= | + | |
| - | <center><math>\begin{matrix} | + | |
| - | 3x^{4} - 2x^3 + 4x^2 + 2x - 3 \quad | \quad x-2 \qquad \quad | + | |
| - | \\ | + | |
| - | \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad \; \, \, \, |-------- \quad | + | |
| - | \\ | + | |
| - | -3x^4 + 6x^3 + 3x^2 \qquad \qquad \quad \quad 3x^{2} + 4x +15 \; \, | + | |
| - | \\ | + | |
| - | -------- \qquad \qquad \qquad \qquad \qquad \qquad | + | |
| - | \\ | + | |
| - | 4x^3 + 7x^2 + 2x -3 \qquad \qquad \quad | + | |
| - | \\ | + | |
| - | -4x^3 + 8x^2 + 4x \qquad \qquad \qquad \quad \; \, | + | |
| - | \\ | + | |
| - | ---------- \qquad \qquad \qquad | + | |
| - | \\ | + | |
| - | ~15x^2 + ~6x -~3 \quad \quad \; \, | + | |
| - | \\ | + | |
| - | -15x^2 + 30x + 15 \quad \quad \; \, \, | + | |
| - | \\ | + | |
| - | --------- \qquad \quad | + | |
| - | \\ | + | |
| - | \quad \ 36x+12 | + | |
| - | \end{matrix}</math></center> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | ===División de un polinomio por (x-a). Regla de Ruffini=== | + | ===Ejercicios propuestos=== |
| - | {{Teorema|titulo= | + | {{ejercicio |
| - | ''Regla de Ruffini'' | + | |titulo=Ejercicios propuestos: ''Teorema del resto'' |
| - | |enunciado= | + | |cuerpo= |
| - | La '''Regla de Ruffini''' nos permite dividir un polinomio entre un binomio de la forma <math>(x-r)\;</math>, siendo <math>r\;</math> un número entero. | + | |
| - | Debemos esta regla al matemático italiano [[Ruffini|Paolo Ruffini]], | + | (Pág. 39) |
| - | |demo= | + | [[Imagen:Red_star.png|12px]] 3a |
| - | Vamos a dividir el polinomio | + | |
| - | :<math>P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0</math> | + | [[Imagen:Yellow_star.png|12px]] 3b |
| - | entre el binomio | ||
| - | |||
| - | :<math>Q(x)=x-r\,\!</math> | ||
| - | |||
| - | para obtener el cociente | ||
| - | |||
| - | :<math>C(x)=b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+\cdots+b_1x+b_0</math> | ||
| - | |||
| - | y el resto <math>s\;</math>. | ||
| - | |||
| - | 1. Trazamos dos líneas a manera de ejes. Cogemos los coeficientes de <math>P(x)\;</math> y los escribimos ordenados. Entonces escribimos <math>r\;</math> en la parte inferior izquierda del eje, encima de la línea: | ||
| - | |||
| - | <center><math>\begin{matrix} | ||
| - | ~~ \, | & a_n & a_{n-1} & \cdots & a_1 & a_0 | ||
| - | \\ | ||
| - | r~ | & & & & & | ||
| - | \\ | ||
| - | ---&-----&-----&-----&-----&----- | ||
| - | \\ | ||
| - | ~~ \, | & & & & & | ||
| - | \\ | ||
| - | ~~ \, | & & & & & | ||
| - | \end{matrix}</math></center> | ||
| - | |||
| - | 2. Pasamos el coeficiente más pegado a la izquierda, <math>a_n\;</math>, justo debajo de la línea, para obtener el primero de los coeficientes <math>b_{n-1}\;</math>: | ||
| - | |||
| - | <center><math>\begin{matrix} | ||
| - | ~~ \, | & a_n & a_{n-1} & \cdots & a_1 & a_0 | ||
| - | \\ | ||
| - | r~ | & & & & & | ||
| - | \\ | ||
| - | ---&-----&-----&-----&-----&----- | ||
| - | \\ | ||
| - | ~~ \, | & a_n & & & & | ||
| - | \\ | ||
| - | ~~ \, | & =b_{n-1} & & & & | ||
| - | \end{matrix}</math></center> | ||
| - | |||
| - | 3. Multiplicamos el número más pegado a la derecha debajo de la línea por r\; y lo escribimos sobre la línea en la primera posición de la derecha: | ||
| - | |||
| - | <center><math>\begin{matrix} | ||
| - | ~~ \, | & a_n & a_{n-1} & \cdots & a_1 & a_0 | ||
| - | \\ | ||
| - | r~ | & & b_{n-1} \ r & & & | ||
| - | \\ | ||
| - | ---&-----&-----&-----&-----&----- | ||
| - | \\ | ||
| - | ~~ \, | & a_n & & & & | ||
| - | \\ | ||
| - | ~~ \, | & =b_{n-1} & & & & | ||
| - | \end{matrix}</math></center> | ||
| - | |||
| - | 4. Añadimos los dos valores que hemos puesto en la misma columna: | ||
| - | |||
| - | <center><math>\begin{matrix} | ||
| - | ~~ \, | & a_n & a_{n-1} & \cdots & a_1 & a_0 | ||
| - | \\ | ||
| - | r~ | & & rb_{n-1} & & & | ||
| - | \\ | ||
| - | ---&-----&------&-----&-----&----- | ||
| - | \\ | ||
| - | ~~ \, | & a_n & a_{n-1}+rb_{n-1} & & & | ||
| - | \\ | ||
| - | ~~ \, | & =b_{n-1} & =b_{n-2} & & & | ||
| - | \end{matrix}</math></center> | ||
| - | |||
| - | 5. Repetimos los pasos 3 y 4 hasta que no tengamos más números: | ||
| - | |||
| - | <center><math>\begin{matrix} | ||
| - | ~~ \, | & a_n & a_{n-1} & \cdots & a_1 & a_0 | ||
| - | \\ | ||
| - | r~ | & & rb_{n-1} & \cdots & rb_1 & rb_0 | ||
| - | \\ | ||
| - | ---&-----&------&-----&-----&----- | ||
| - | \\ | ||
| - | ~~ \, | & a_n & a_{n-1}+rb_{n-1} & \cdots & a_1+rb_1 & a_0 +rb_0 | ||
| - | \\ | ||
| - | ~~ \, | & =b_{n-1} & =b_{n-2} & \cdots & =b_0 & =s | ||
| - | \end{matrix}</math></center> | ||
| - | |||
| - | |||
| - | Los valores <math>b_i\;</math> son los coeficientes del polinomio cociente <math>C(x)\;</math>, cuyo grado será un grado menor que el del dividendo <math>P(x)\;</math>. El resto será <math>s\;</math>. | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{Ejemplo | ||
| - | |titulo=Ejemplo: ''Regla de Ruffini'' | ||
| - | |enunciado= | ||
| - | :Divide los polinomios usando la regla de [[Ruffini]]: | ||
| - | ::<math> P(x)=7x^4-5x^3-4x^2+6x-1\,\! </math> | ||
| - | ::<math> Q(x)=x-2\,\! </math> | ||
| - | |sol= | ||
| - | {{Tabla50 | ||
| - | |celda1= | ||
| - | <center><pre> | ||
| - | | 7 -5 -4 6 -1 | ||
| - | | | ||
| - | 2| 14 18 28 68 | ||
| - | --|------------------- | ||
| - | | 7 9 14 34 |67 | ||
| - | |____ | ||
| - | </pre></center> | ||
| - | |||
| - | El resultado significa que: | ||
| - | *'''Cociente de la división:''' <math>C(x)=7x^3+9x^2+14x+34\,\!</math> | ||
| - | *'''Resto:''' <math>r=67\,\!</math> | ||
| - | |||
| - | |celda2= | ||
| - | {{p}} | ||
| - | :'''Operaciones:''' | ||
| - | :* <math>2 \cdot 7=14\,\!</math> | ||
| - | |||
| - | :* <math>-5+14=9\,\!</math> | ||
| - | |||
| - | :* <math>2 \cdot 9 =18\,\!</math> | ||
| - | |||
| - | :* <math>-4+18=14\,\!</math> | ||
| - | |||
| - | :* <math>2\cdot 14=28\,\!</math> | ||
| - | |||
| - | :* <math>6+28=34\,\!</math> | ||
| - | |||
| - | :* <math>2 \cdot 34=68\,\!</math> | ||
| - | |||
| - | :* <math>-1+68=67\,\!</math> | ||
| - | |||
| - | }} | ||
| - | }} | ||
| - | |||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Calculadora |
Tabla de contenidos |
Regla de Ruffini
División de un polinomio por (x-a)
Regla de Ruffini
La Regla de Ruffini es un procedimiento que nos permite dividir un polinomio entre un binomio de la forma 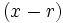 .
.
Debemos esta regla al matemático italiano Paolo Ruffini,
Procedimiento:
Vamos a dividir el polinomio
entre el binomio
para obtener el cociente
y el resto 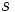 .
.
1. Trazamos dos líneas a manera de ejes. Cogemos los coeficientes de  y los escribimos ordenados. Entonces escribimos
y los escribimos ordenados. Entonces escribimos  en la parte inferior izquierda del eje, encima de la línea:
en la parte inferior izquierda del eje, encima de la línea:
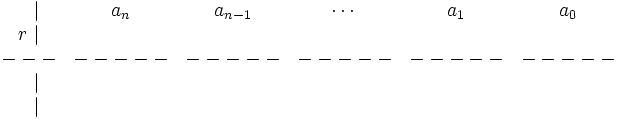
2. Pasamos el coeficiente más pegado a la izquierda,  , justo debajo de la línea, para obtener el primero de los coeficientes
, justo debajo de la línea, para obtener el primero de los coeficientes 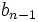 :
:
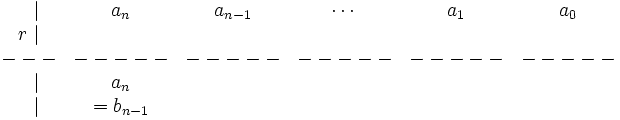
3. Multiplicamos el número más pegado a la derecha debajo de la línea por  y lo escribimos sobre la línea en la primera posición de la derecha:
y lo escribimos sobre la línea en la primera posición de la derecha:
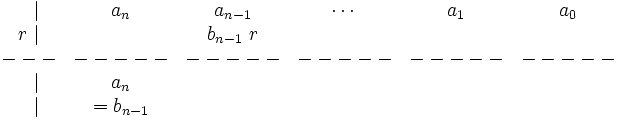
4. Añadimos los dos valores que hemos puesto en la misma columna:
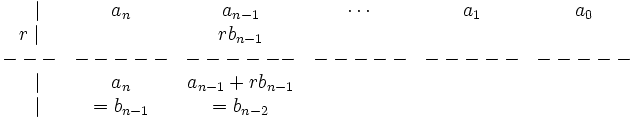
5. Repetimos los pasos 3 y 4 hasta que no tengamos más números:
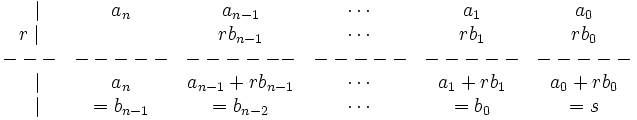
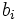 son los coeficientes del polinomio cociente
son los coeficientes del polinomio cociente 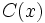 , cuyo grado será un grado menor que el del dividendo
, cuyo grado será un grado menor que el del dividendo  . El resto será
. El resto será 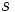 .
.Ejemplo: Regla de Ruffini
Divide los polinomios usando la regla de Ruffini:
| 7 -5 -4 6 -1
|
2| 14 18 28 68
--|-------------------
| 7 9 14 34 |67
|____
El resultado significa que:
|
|
Regla de Ruffini. Ejemplos.
Regla de Ruffini: Método rápido para realizar divisiones de polinomios entre binomios del tipo (x - a). Ejemplos.
La regla de Ruffini nos permite determinar supersónicamente el cociente y el resto de la división entre un polinomio P(x) y el polinomio Q(x) = x - a.
Cómo se aplica la Regla de Ruffini.
División de polinomios por el método de Ruffini para divisores del tipo (x-a).
Ejemplo de división de polinomios usando la regla de Ruffini.
2 ejemplos de división de polinomios usando la regla de Ruffini.
2 ejemplos de división mediante la regla de Ruffini
Otros 2 ejemplos de aplicación de la regla de Ruffini
Divide 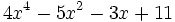 entre
entre 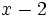 .
.
a) Divide 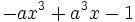 entre
entre 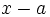
b) Divide 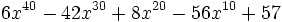 entre
entre 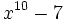
Divide los siguientes polinomios utilizando la regla de Ruffini:
- 1a)
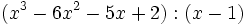
- 1b)
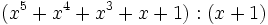
- 1c)
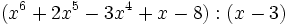
- 1d)
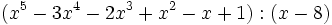
- 1e)
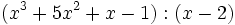
- 1f)
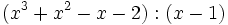
Divide los siguientes polinomios utilizando la regla de Ruffini:
- 1g)
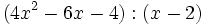
- 1h)
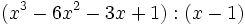
- 1i)
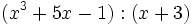
- 1j)
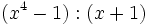
- 1k)
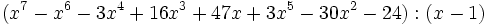
- 1l)
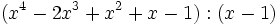
Divide los siguientes polinomios utilizando la regla de Ruffini:
- 2a)
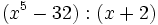
- 2b)
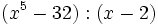
- 2c)
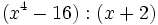
- 2d)
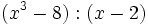
- 2e)
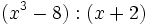
Divide los siguientes polinomios utilizando la regla de Ruffini:
- 2f)
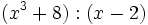
- 2g)
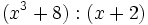
- 2h)
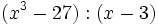
- 2i)
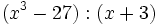
- 2j)
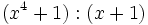
Divide los siguientes polinomios utilizando la regla de Ruffini:
- a)
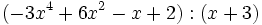
- b)
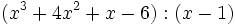
- c)
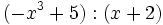
Ejercicios de autoevaluación sobre la regla de Ruffini.
División de un polinomio por (mx+n)
Proposición
Para dividir un polinomio  por un binomio del tipo
por un binomio del tipo 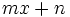 efectuaremos la división por
efectuaremos la división por 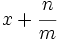 (usando Ruffini pondríamos
(usando Ruffini pondríamos 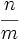 en el lado izquierdo de la línea vertical), con lo que obtendríamos un cociente
en el lado izquierdo de la línea vertical), con lo que obtendríamos un cociente 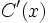 y un resto
y un resto  .
.
Entonces el cociente 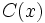 y el resto
y el resto 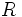 de la división del polinomio entre
de la división del polinomio entre 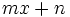 serán:
serán:
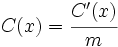 ;
; 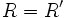
Ejercicios propuestos
|
Ejercicios propuestos: Regla de Ruffini |
Teorema del resto
Teorema del Resto
El valor que toma un polinomio,  , cuando hacemos
, cuando hacemos  , coincide con el resto de la división de
, coincide con el resto de la división de  entre
entre 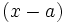 . Es decir,
. Es decir, 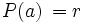 , donde
, donde  es el resto de dicha división.
es el resto de dicha división.
Esto se deduce directamente de una de las propiedades de la división, la que dice que:
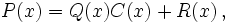
donde  es el dividendo,
es el dividendo,  el divisor,
el divisor, 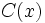 el cociente y
el cociente y 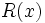 el resto y verificándose además, que el grado de
el resto y verificándose además, que el grado de 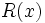 es menor que el grado de
es menor que el grado de  .
.
En efecto, si tomamos el divisor 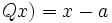 , entonces
, entonces 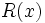 tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar
tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar  , y la fórmula anterior se convierte en:
, y la fórmula anterior se convierte en:
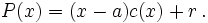
Tomando el valor 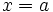 se obtiene que:
se obtiene que:
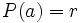
Ejemplo: Teorema del Resto
Calcula el resto de dividir el polinomio 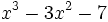 entre
entre 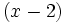
Primer método:
Bastará calcular 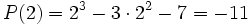
Así el resto será 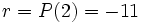
Segundo método:
Usando la regla de Ruffini:
| 1 -3 0 -7
|
2| 2 -2 -4
--|----------------
| 1 -1 -2 |-11
|____
Así, el resto de la división es -11, y por el teorema del resto, P(2) = -11.Teorema del resto. Ejemplos.
Si P(x) es un polinomio de grado no inferior a 1, el resto de la división P(x)/(x-a) es el número P(a) que se obtiene al sustituir "x" por "a" en P(x). La división P(x)/(x-a) es "exacta" si P(a) = 0; y en tal caso se dice que "a" es un "cero" o "raíz" del polinomio P(x), o una solución de la ecuación P(x) = 0.
- Teorema del resto para la división de un polinomio entre un binomio del tipo (ax+b).
- Como ejemplo, también resolveremos los siguientes ejercicios:
- 1) Halla el resto de dividir el polinomio
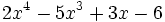 entre el binomio
entre el binomio 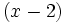 .
.
- 2) Halla el resto de dividir el polinomio
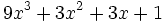 entre el binomio
entre el binomio 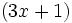 .
.
Halla el resto de la división del polinomio 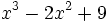 entre
entre 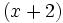 .
.
Halla el valor de  para que la división del polinomio
para que la división del polinomio 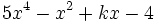 entre
entre 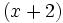 sea exacta.
sea exacta.
1) Halla el resto de la división del polinomio 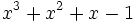 entre
entre 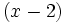 ,
, 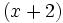 ,
, 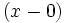 y
y 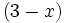 .
.
2) Determina el valor de k para que el polinomio 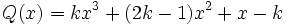 sea divisible por
sea divisible por 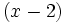 .
.
3) Sea 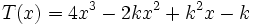 . Halla el valor de k para que el resto de la división de
. Halla el valor de k para que el resto de la división de 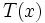 entre
entre 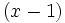 sea igual a 2.
sea igual a 2.
a) Halla el resto de la división de 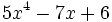 entre
entre 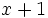 .
.
b) y c) Otros dos ejercicios de nivel superior.
Ejercicios de autoevaluación sobre el teorema del resto.
Ejercicios propuestos
|
Ejercicios propuestos: Teorema del resto |