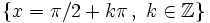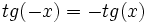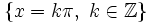Funciones trigonométricas o circulares (1ºBach)
De Wikipedia
| Revisión de 07:59 18 dic 2017 Coordinador (Discusión | contribuciones) (→Modelando con funciones trigonométricas) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Función tangente) |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Funciones trigonométricas== | ==Funciones trigonométricas== | ||
| - | Vamos a estudiar las funciones que se obtienen a partir de las razones trigonométricas de un ángulo '''x''' al hacer variar éste. Dicho ángulo se suele expresar en radianes. | + | {{Funciones trigonométricas}} |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver como se representan las funciones trigonométricas. | + | |
| - | |enlace=[http://ggbm.at/UHsRFWbu Funciones trigonométricas] | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace_fonemato | + | |
| - | |titulo1=Gráficas de las funciones seno y coseno | + | |
| - | |duracion=9'04" | + | |
| - | |sinopsis=Estudio gráfico de las funciones seno y coseno. | + | |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/20-graficas-de-las-funciones-seno-y-coseno-5#.VCrSixa7ZV8 | + | |
| - | }} | + | |
| ===Función seno=== | ===Función seno=== | ||
| - | {{Tabla50|celda2=<center>'''Función seno''' (sinusoide).{{p}}[[Imagen:funcionseno.png|380px|]]<br>Los valores en el eje x están expresados en radianes</center> | + | {{Función seno}} |
| - | |celda1= | + | |
| - | {{Caja_Amarilla|texto=Se define la función '''seno''' como | + | |
| - | + | ||
| - | <center><math>f(x)=sen(x) \, , \ x \in \mathbb{R}</math></center> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Teorema_sin_demo|titulo=Propiedades de la función seno|enunciado= | + | |
| - | *'''Dominio:''' <math>\mathbb{R}</math> | + | |
| - | *'''Recorrido:''' <math>[-1, 1]\,</math> | + | |
| - | *'''Periodicidad:''' Es periódica, con período <math>2 \pi \,</math>. | + | |
| - | *'''Continuidad:''' Es continua en su dominio, <math>\mathbb{R}</math>. | + | |
| - | *'''Simetrías:''' Es impar, pués <math>sen(-x)=-sen(x)\,</math> | + | |
| - | *'''Cortes con eje X:''' <math>\left \{ x=0+ \pi k \, , \ k \in \mathbb{Z} \right \}</math> | + | |
| - | *'''Máximos:''' <math>\left \{ x=\pi / 2+2 \pi k \, , \ k \in \mathbb{Z} \right \}</math> | + | |
| - | *'''Mínimos:''' <math>\left \{ x=3 \pi /2 +2 \pi k \, , \ k \in \mathbb{Z} \right \}</math> | + | |
| - | *'''Crecimiento:''' | + | |
| - | **Crece en los intervalos <math>\big( 3 \pi / 2+2 \pi (k-1) , \, \pi /2 +2 \pi k \big), \ k \in \mathbb{Z}</math>. | + | |
| - | **Decrece en los intervalos <math>\big( \pi / 2+2 \pi k , \, 3 \pi /2 +2 \pi k \big), \ k \in \mathbb{Z}</math>. | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{Videotutoriales|titulo=La función seno|enunciado= | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Tutorial 1 | + | |
| - | |duracion=23'02" | + | |
| - | |sinopsis=Definición, representación y análisis de la función seno. | + | |
| - | |url1=https://www.youtube.com/watch?v=PpT9jA8AOUY | + | |
| - | }} | + | |
| - | {{Video_enlace_matemovil | + | |
| - | |titulo1=Tutorial 2 | + | |
| - | |duracion=27'53" | + | |
| - | |sinopsis=Definición, representación y análisis de la función seno. Ejercicios. | + | |
| - | |url1=https://www.youtube.com/watch?v=JwGW8YyNp4M&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=57 | + | |
| - | }} | + | |
| - | {{Video_enlace_khan | + | |
| - | |titulo1=Tutorial 3 | + | |
| - | |duracion=9'23" | + | |
| - | |sinopsis=Dominio, rango y representación de la función seno. | + | |
| - | |url1=https://www.youtube.com/watch?v=wnokkV3NqSU | + | |
| - | }} | + | |
| - | }} | + | |
| ===Función coseno=== | ===Función coseno=== | ||
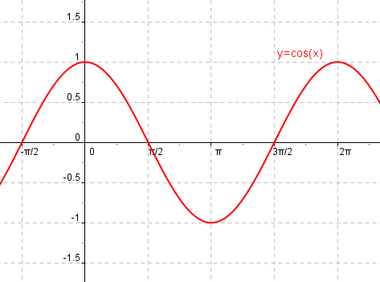
| - | {{Tabla50|celda2=<center>'''Función coseno''' (cosinusoide).{{p}}[[Imagen:funcioncoseno.png|380px|]]<br>Los valores en el eje x están expresados en radianes</center> | + | {{Función coseno}} |
| - | |celda1= | + | |
| - | {{Caja_Amarilla|texto=Se define la función '''coseno''' como | + | |
| - | + | ||
| - | <center><math>f(x)=cos(x) \, , \ x \in \mathbb{R}</math></center> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Teorema_sin_demo|titulo=Propiedades de la función coseno|enunciado= | + | |
| - | *'''Dominio:''' <math>\mathbb{R}</math> | + | |
| - | *'''Recorrido:''' <math>[-1, 1]\,</math> | + | |
| - | *'''Periodicidad:''' Es periódica, con período <math>2 \pi \,</math>. | + | |
| - | *'''Continuidad:''' Es continua en su dominio, <math>\mathbb{R}</math>. | + | |
| - | *'''Simetrías:''' Es par, pués <math>cos(-x)=cos(x)\,</math> | + | |
| - | *'''Cortes con eje X:''' <math>\left \{ x=\pi /2 + \pi k \, , \ k \in \mathbb{Z} \right \}</math> | + | |
| - | *'''Máximos:''' <math>\left \{ x=2 \pi k \, , \ k \in \mathbb{Z} \right \}</math> | + | |
| - | *'''Mínimos:''' <math>\left \{ x=\pi (2k+1) \, , \ k \in \mathbb{Z} \right \}</math> | + | |
| - | *'''Crecimiento:''' | + | |
| - | **Crece en los intervalos <math>\big( \pi (2k-1) , \, 2 \pi k \big), \ k \in \mathbb{Z}</math>. | + | |
| - | **Decrece en los intervalos <math>\big( 2 \pi k , \, \pi (2k+1) \big), \ k \in \mathbb{Z}</math>. | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Videotutoriales|titulo=La función coseno|enunciado= | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Tutorial 1 | + | |
| - | |duracion=26'21" | + | |
| - | |sinopsis=Definición, representación y análisis de la función coseno. | + | |
| - | |url1=https://www.youtube.com/watch?v=8z0M2hnCJIY | + | |
| - | }}{{Video_enlace_matemovil | + | |
| - | |titulo1=Tutorial 2 | + | |
| - | |duracion=30'13" | + | |
| - | |sinopsis=Definición, representación y análisis de la función coseno. Ejercicios. | + | |
| - | |url1=https://www.youtube.com/watch?v=Dgpsd_CwZfs&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=58 | + | |
| - | }} | + | |
| - | }} | + | |
| ===Función tangente=== | ===Función tangente=== | ||
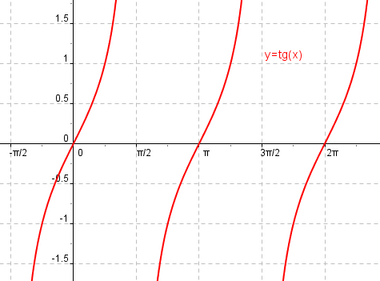
| - | {{Tabla50|celda2=<center>'''Función tangente'''.{{p}}[[Imagen:funciontg.png|380px|]]<br>Los valores en el eje x están expresados en radianes</center> | + | {{Función tangente}} |
| - | |celda1= | + | |
| - | {{Caja_Amarilla|texto=Se define la función '''coseno''' como | + | |
| - | + | ||
| - | <center><math>f(x)=tg(x) \, , \quad x \in \mathbb{R}-\left \{ \pi /2 + k \pi \, , \ k \in \mathbb{Z} \right \}</math></center> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Teorema_sin_demo|titulo=Propiedades de la función tangente|enunciado= | + | |
| - | *'''Dominio:''' <math>\mathbb{R}-\left \{ \pi /2 + k \pi \, , \ k \in \mathbb{Z} \right \}</math> | + | |
| - | *'''Recorrido:''' <math>\mathbb{R}</math> | + | |
| - | *'''Periodicidad:''' Es periódica, con período <math>\pi \,</math>. | + | |
| - | *'''Continuidad:''' Es continua en su dominio. Tiene discontinuidades en <math>\left \{ x=\pi /2 + k \pi \, , \ k \in \mathbb{Z} \right \}</math> | + | |
| - | *'''Simetrías:''' Es impar, pués <math>tg(-x)=-tg(x)\,</math> | + | |
| - | *'''Cortes con eje X:''' <math>\left \{ x=k \pi , \ k \in \mathbb{Z} \right \}</math> | + | |
| - | *'''Máximos:''' No tiene | + | |
| - | *'''Mínimos:''' No tiene | + | |
| - | *'''Crecimiento:''' Creciente en cada intervalo que compone sus dominio. | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Videotutoriales|titulo=La función tangente|enunciado= | + | |
| - | {{Video_enlace_matemovil | + | |
| - | |titulo1=Tutorial 1 | + | |
| - | |duracion=26'00" | + | |
| - | |sinopsis=Definición, representación y análisis de la función tangente. Ejercicios. | + | |
| - | |url1=https://www.youtube.com/watch?v=-hISqPei4G4&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=59 | + | |
| - | }} | + | |
| - | {{Video_enlace_khan | + | |
| - | |titulo1=Tutorial 2 | + | |
| - | |duracion=10'13" | + | |
| - | |sinopsis=Representación de la función tangente | + | |
| - | |url1=https://www.youtube.com/watch?v=lg6xE2_hQW4 | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| Línea 230: | Línea 111: | ||
| ==Transformaciones de funciones trigonométricas== | ==Transformaciones de funciones trigonométricas== | ||
| - | {{Videotutoriales|titulo=Traslaciones|enunciado= | + | Para este apartado necesitarás ver primero: [[Transformaciones elementales de funciones (1ºBach)|Transformaciones elementales de funciones]]. |
| - | {{Video_enlace_abel | + | {{p}} |
| - | |titulo1=Translación vertical de una función seno | + | {{Videotutoriales|titulo=Transformaciones de funciones trigonométricas|enunciado= |
| - | |duracion=15'39" | + | '''Traslaciones:''' |
| - | |sinopsis=Representa la función: <math>f(x)=2+sen(x)\;</math>. | + | |
| - | |url1=https://www.youtube.com/watch?v=XKIWDDJAXog | + | |
| - | }} | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Translación vertical de una función coseno | + | |
| - | |duracion=14'01" | + | |
| - | |sinopsis=Representa la función: <math>f(x)=1+cos(x)\;</math>. | + | |
| - | |url1=https://www.youtube.com/watch?v=r1m_trSRtE4 | + | |
| - | }} | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Traslación horizontal de una función coseno | + | |
| - | |duracion=16'45" | + | |
| - | |sinopsis=Representa la función: <math>f(x)=cos(2x+ \cfrac{\pi}{2})</math>. | + | |
| - | |url1=https://www.youtube.com/watch?v=C0u1ajYa6Ks | + | |
| - | }} | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Traslación horizontal de una función seno | + | |
| - | |duracion=19'09" | + | |
| - | |sinopsis=Representa la función: <math>f(x)=sen(2x+ \cfrac{\pi}{2})</math>. | + | |
| - | |url1=https://www.youtube.com/watch?v=CTRR0d56ePo | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{Videotutoriales|titulo=Dilataciones y contracciones|enunciado= | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Dilataciones y contracciones horizontales de una función coseno | + | |
| - | |duracion=35'01" | + | |
| - | |sinopsis=Representa las funciones: | + | |
| - | 1) <math>f(x)=cos(2x)\;</math> | + | {{Traslaciones de funciones trigonometricas}} |
| - | 2) <math>f(x)=cos(\cfrac{x}{2})\;</math> | + | ---- |
| - | |url1=https://www.youtube.com/watch?v=4PDsxOGHwcU | + | '''Dilataciones y contracciones:''' |
| - | }} | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Dilataciones y contracciones verticales de una función coseno | + | |
| - | |duracion=34'39" | + | |
| - | |sinopsis=Representa las funciones: | + | |
| - | 1) <math>f(x)=2\,cos(x)\;</math> | + | {{Dilataciones y contracciones funciones trigonometricas}} |
| - | 2) <math>f(x)=\cfrac{1}{2}\,cos(x)\;</math> | + | ---- |
| - | |url1=https://www.youtube.com/watch?v=8tVsTo2vrYk | + | '''Ejercicios:''' |
| - | }} | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Dilataciones y contracciones de una función seno | + | |
| - | |duracion=40'12" | + | |
| - | |sinopsis=Representa las funciones: | + | |
| - | 1) <math>f(x)=2\,sen(x)\;</math> | ||
| - | |||
| - | 2) <math>f(x)=sen(2x)\;</math> | ||
| - | |||
| - | 2) <math>f(x)=3\,sen(\cfrac{x}{2})\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=PIFBQhc0ebQ | ||
| - | }} | ||
| - | }} | ||
| - | {{Videotutoriales|titulo=Ejercicios|enunciado= | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| Línea 319: | Línea 154: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Info|texto=Más información en: | + | {{Info|texto=Más información en: [http://quiz.uprm.edu/tutorials_master/fn_trig_trans/fn_trig_trans.html {{b}}Transformaciones de funciones trigonométricas] |
| - | *[[Transformaciones elementales de funciones (1ºBach)|Transformaciones elementales de funciones]] | + | |
| - | *[http://quiz.uprm.edu/tutorials_master/fn_trig_trans/fn_trig_trans.html {{b}}Transformaciones de funciones trigonométricas] | + | |
| }} | }} | ||
| Línea 366: | Línea 199: | ||
| |titulo1=Ejercicio 4 | |titulo1=Ejercicio 4 | ||
| |duracion=7'44" | |duracion=7'44" | ||
| - | |sinopsis=El día más largo del año en Juneau, Alaska, es el 21 de junio, el cual dura 1096.5 minutos. Medio año después, cuando los días son más cortos, éstos duran alrededor de 382.5 minutos. | + | |sinopsis=Modelar funciones sinusoidales con desplazamiento de fase: |
| + | |||
| + | El día más largo del año en Juneau, Alaska, es el 21 de junio, el cual dura 1096.5 minutos. Medio año después, cuando los días son más cortos, éstos duran alrededor de 382.5 minutos. | ||
| Sabiendo que no es un año bisiesto y el día 21 de junio es el día 172 del año, encuentra la función trigonométrica que modele la duración ''L'' del día ''t'' del año. | Sabiendo que no es un año bisiesto y el día 21 de junio es el día 172 del año, encuentra la función trigonométrica que modele la duración ''L'' del día ''t'' del año. | ||
| Línea 387: | Línea 222: | ||
| {{AI_Khan | {{AI_Khan | ||
| |titulo1=Autoevaluación 3 | |titulo1=Autoevaluación 3 | ||
| - | |descripcion=Modelar con funciones sinusoidales: desplazamiento de fase. | + | |descripcion=Modelar con funciones sinusoidales con desplazamiento de fase. |
| |url1=https://es.khanacademy.org/math/trigonometry/trig-function-graphs/constructing-sinusoids/e/modeling-with-periodic-functions-2 | |url1=https://es.khanacademy.org/math/trigonometry/trig-function-graphs/constructing-sinusoids/e/modeling-with-periodic-functions-2 | ||
| Línea 395: | Línea 230: | ||
| {{Info|texto=Más información en: [http://quiz.uprm.edu/tutorials_master/fn_trig_mod/fn_trig_mod.html Modelando con funciones trigonométricas] | {{Info|texto=Más información en: [http://quiz.uprm.edu/tutorials_master/fn_trig_mod/fn_trig_mod.html Modelando con funciones trigonométricas] | ||
| }} | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Funciones trigonométricas recíprocas o funciones arco== | ||
| + | *Véase: [[Funciones arco (1ºBach)|Funciones arco]]. | ||
| {{p}} | {{p}} | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Funciones trigonométricas
Vamos a estudiar las funciones que se obtienen a partir de las razones trigonométricas de un ángulo x al hacer variar éste. Dicho ángulo se suele expresar en radianes.
En esta escena podrás ver como se representan las funciones trigonométricas.
Estudio gráfico de las funciones seno y coseno.
Función seno
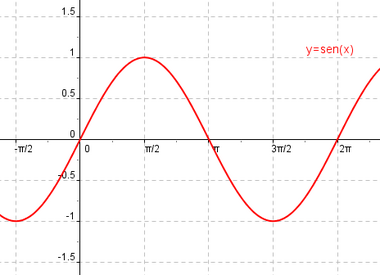
Se define la función seno como 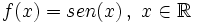 |
Definición, representación y análisis de la función seno.
Definición, representación y análisis de la función seno. Ejercicios.
Dominio, rango y representación de la función seno.
Función coseno
Se define la función coseno como 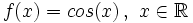 |
Definición, representación y análisis de la función coseno.
Definición, representación y análisis de la función coseno. Ejercicios.
Función tangente
Se define la función coseno como 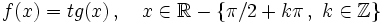 Propiedades de la función tangente
|
Definición, representación y análisis de la función tangente. Ejercicios.
Representación de la función tangente
Línea media, amplitud y período de las funciones trigonométricas
Línea media, amplitud y periodicidad de las funciones sinusoidales.
Estudio de la periodicidad de las funciones trigonométricas directas e inversas.
Amplitud y periodo de la función seno.
Amplitud de la función coseno.
Período de la función coseno.
Determina la amplitud y el período de la función 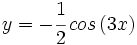 .
.
Repaso sobre línea media, amplitud y periodo de funciones sinusoidales.
La línea media de funciones sinusoidales a partir de sus gráficas.
La amplitud de funciones sinusoidales a partir de sus gráficas.
Línea media de funciones sinusoidales a partir de sus ecuaciones.
Amplitud de funciones sinusoidales a partir de sus ecuaciones.
El periodo de funciones sinusoidales a partir de sus gráficas.
Periodo de funciones sinusoidales a partir de sus ecuaciones.
Transformaciones de funciones trigonométricas
Para este apartado necesitarás ver primero: Transformaciones elementales de funciones.
Traslaciones:
Representa la función: 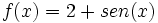 .
.
Representa la función: 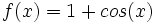 .
.
Representa la función: 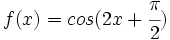 .
.
Representa la función: 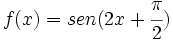 .
.
Dilataciones y contracciones:
Representa las funciones:
1) 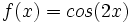
2) 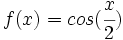
Representa las funciones:
1) 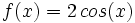
2) 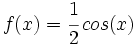
Representa las funciones:
1) 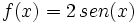
2) 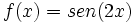
2) 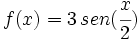
Ejercicios:
Representa la función: 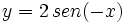 en el intervalo
en el intervalo ![\left[ -2\pi, 2\pi \right]](/wikipedia/images/math/4/d/5/4d58643048935ec32762a193a3ad1a8e.png) .
.
Representa la función: 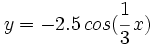 en el intervalo
en el intervalo ![\left[ 0, 6\pi \right]](/wikipedia/images/math/3/e/4/3e4e9546ff9f69814b61b915171b9ddb.png) .
.
Grafica funciones sinusoidales en la cuadrícula interactiva.
Grafica funciones sinusoidales en la cuadrícula interactiva (desplazamiento de fase).
Modelando con funciones trigonométricas
En este apartado vamos a ver cómo se obtiene la expresión analítica de una función trigonométrica que nos permita representar una determinada situación, partiendo de cierta información verbal o gráfica.
Escribe la ecuación de la función trigonométrica dada en el video.
En Johannesburgo, en junio, la temperatura mínima diaria usual es aproximadamente de 3ºC, y la temperatura máxima diaria alrededor de 18ºC. La temperatura se ubica justo a la mitad entre la máxima y la mínima diaria, tanto a las 10 a.m. como a las 10 p.m., alcanzándose la temperatura máxima por la tarde. Encuentra una función trigonométrica que modele la temperatura T en Johannesburgo a las t horas después de media noche.
El día más caluroso del año, en promedio, en Santiago de Chile, es el 7 de enero cuando la media de la temperatura máxima es de 29ºC. El día más frio del año tiene una temperatura máxima media de 14ºC.
Usa una función trigonométrica para modelar la temperatura en Santiago de Chile, usando 365 días como la duración de un año y partiendo del 7 de enero. Recuerda que el 7 de enero es verano en Santiago.
¿Cuántos días después del 7 de enero es el primer día de primavera cuando la temperatura máxima alcanza 20ºC?
Continuación del ejercicio anterior:
El día más caluroso del año, en promedio, en Santiago de Chile, es el 7 de enero cuando la media de la temperatura máxima es de 29ºC. El día más frio del año tiene una temperatura máxima media de 14ºC.
Usa una función trigonométrica para modelar la temperatura en Santiago de Chile, usando 365 días como la duración de un año y partiendo del 7 de enero. Recuerda que el 7 de enero es verano en Santiago.
¿Cuántos días después del 7 de enero la temperatura máxima alcanza 20ºC (primer día de primavera)?
Modelar funciones sinusoidales con desplazamiento de fase:
El día más largo del año en Juneau, Alaska, es el 21 de junio, el cual dura 1096.5 minutos. Medio año después, cuando los días son más cortos, éstos duran alrededor de 382.5 minutos.
Sabiendo que no es un año bisiesto y el día 21 de junio es el día 172 del año, encuentra la función trigonométrica que modele la duración L del día t del año.
Escribe la ecuación de la función trigonométrica correspondiente a unos datos dados.
Modelar con funciones sinusoidales.
Modelar con funciones sinusoidales con desplazamiento de fase.
Funciones trigonométricas recíprocas o funciones arco
- Véase: Funciones arco.
Actividades y videotutoriales
Averigua los puntos de intersección de las funciones seno y coseno en el primer giro.
En esta escena podrás ver como se obtiene el ángulo conocida una razón, de forma gráfica, utilizando la representación gráfica de las funciones trigonométricas.
|
Actividad: Funciones trigonométricas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|

![[-1, 1]\,](/wikipedia/images/math/5/8/1/581a26dec23e9f937a02a278e20fc9c3.png)
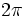 .
.
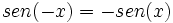
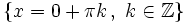
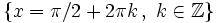

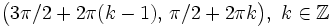 .
.
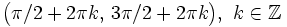 .
.
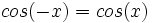
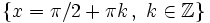
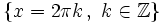
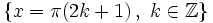
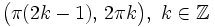 .
.
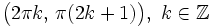 .
.
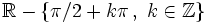
 .
.