Plantilla:Def progresion aritmetica
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:28 27 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Una '''progresión aritmética''' es una sucesión de números en la que cada término se obtiene sumando al anterior una cantidad fija, <math>d\;\!</math>, que llamaremos '''diferencia'''. | + | Una '''progresión aritmética''' es una sucesión de números en la que cada término se obtiene sumando al anterior una cantidad fija, {{sube|porcentaje=20%|contenido=<math>d\;\!</math>}}, que llamaremos '''diferencia'''. |
| + | |||
| + | Escrito en forma recursiva: | ||
| + | |||
| + | <center><math>a_n=a_{n-1} + d \ , \ \forall n>1</math></center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Por ejemplo: | + | Por ejemplo, la sucesión <math>u_n\;</math>: |
| <center>[[Imagen:prog_aritmetica.png]]</center> | <center>[[Imagen:prog_aritmetica.png]]</center> | ||
| - | es una progresión aritmética con diferencia d=4. | + | es una progresión aritmética con diferencia {{sube|porcentaje=20%|contenido=<math>d = 4\;</math>}}. |
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Progresiones aritméticas|enunciado= | {{Videotutoriales|titulo=Progresiones aritméticas|enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=3´42" | ||
| + | |url1=https://youtu.be/JD2Gmq6ux3g?list=PLwCiNw1sXMSBhPnvO9i-OTkq_sZu71YLG | ||
| + | |sinopsis=Progresiones aritméticas: definición y ejemplos. | ||
| + | }} | ||
| + | ---- | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| Línea 17: | Línea 28: | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| |titulo1=Ejercicio 2 | |titulo1=Ejercicio 2 | ||
| - | |duracion=6´39" | ||
| - | |url1=https://youtu.be/_6WrqWRbcxI | ||
| - | |sinopsis= | ||
| - | #Una progresión aritmética tiene como término general <math>a_i=4+3(i-1)\;</math>, halla el término <math>a_{20}\;</math>. | ||
| - | #Halla el término <math>a_5\;</math> de una progresión aritmética que viene dada por la siguiente ley de recurrencia: | ||
| - | :<math>\begin{cases}a_1=-7 \\ a_i=a_{i-1}-2 \ , \ \forall i>1 \end{cases}</math> | ||
| - | }} | ||
| - | {{Video_enlace_khan | ||
| - | |titulo1=Ejercicio 3 | ||
| |duracion=3´41" | |duracion=3´41" | ||
| |url1=https://youtu.be/avamSPbNDmE | |url1=https://youtu.be/avamSPbNDmE | ||
| Línea 54: | Línea 56: | ||
| {{AI_Khan | {{AI_Khan | ||
| |titulo1=Autoevaluación 2 | |titulo1=Autoevaluación 2 | ||
| - | |descripcion=Usa fórmulas de sucesiones aritméticas. | ||
| - | |url1=http://es.khanacademy.org/math/algebra/sequences/introduction-to-arithmetic-squences/e/arithmetic_sequences_2 | ||
| - | }} | ||
| - | {{AI_Khan | ||
| - | |titulo1=Autoevaluación 3 | ||
| |descripcion=Fórmulas recursivas para sucesiones aritméticas. | |descripcion=Fórmulas recursivas para sucesiones aritméticas. | ||
| |url1=http://es.khanacademy.org/math/algebra/sequences/constructing-arithmetic-sequences/e/recursive-formulas-for-arithmetic-sequences | |url1=http://es.khanacademy.org/math/algebra/sequences/constructing-arithmetic-sequences/e/recursive-formulas-for-arithmetic-sequences | ||
Revisión actual
Una progresión aritmética es una sucesión de números en la que cada término se obtiene sumando al anterior una cantidad fija, 
, que llamaremos diferencia.
Escrito en forma recursiva:
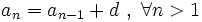
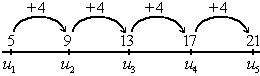
Por ejemplo, la sucesión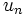 
:
es una progresión aritmética con diferencia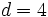 
.
Tutorial (3´42") Sinopsis:Progresiones aritméticas: definición y ejemplos.
Ejercicio 1 (2´08") Sinopsis: Determina el quinto término de la siguiente progresión aritmética: {-3, -7, -11, -15, ...}
Ejercicio 2 (3´41") Sinopsis: Dados los términos de una progresión aritmética, completar la fórmula de recurrencia.
Actividad 1 Descripción: Actividades en las que aprenderás el concepto de progresión aritmética y a cómo identificarlas.
Actividad 2 Descripción: Actividades de introducción a las sucesiones aritméticas.
Actividad 3 Descripción: Fórmulas recursivas para sucesiones aritméticas.
Autoevaluación 1 Descripción: Extiende sucesiones aritméticas.
Autoevaluación 2 Descripción: Fórmulas recursivas para sucesiones aritméticas.
