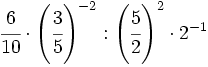Plantilla:Videos ejemplos propiedades potencias racionales
De Wikipedia
| Revisión de 17:19 1 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 16: | Línea 16: | ||
| |url1=https://www.youtube.com/watch?v=wfjPJOev36o&index=9&list=PL773F27163628CA1F | |url1=https://www.youtube.com/watch?v=wfjPJOev36o&index=9&list=PL773F27163628CA1F | ||
| }} | }} | ||
| - | ---- | + | {{Video_enlace_escuela |
| + | |titulo1=Tutorial 3a | ||
| + | |duracion=6'20" | ||
| + | |sinopsis=Producto de potencias de fracciones con la misma base. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=9-jqLUrkBCQ&index=4&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY- | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 3b | ||
| + | |duracion=6'01" | ||
| + | |sinopsis=Cociente de potencias de fracciones con la misma base. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=l4fBWy8UGe0&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=5 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 3c | ||
| + | |duracion=4'56" | ||
| + | |sinopsis=Potencia de otra potencia de una fracción. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=mVJCGkYLXec&index=6&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY- | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 3d | ||
| + | |duracion=6'08" | ||
| + | |sinopsis=Potencia de un producto de fracciones. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=L5ssdjBM1xk&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=7 | ||
| + | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Producto de potencias de la misma base | + | |titulo1=Tutorial 4a |
| |duracion=3'00" | |duracion=3'00" | ||
| - | |sinopsis=<math>a^n \cdot a^m=a^{m+n}\;</math>. Ejemplos. | + | |sinopsis=Producto de potencias de la misma base: <math>a^n \cdot a^m=a^{m+n}\;</math>. Ejemplos. |
| |url1=https://www.youtube.com/watch?v=SDxP8TZMFnw&index=1&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3 | |url1=https://www.youtube.com/watch?v=SDxP8TZMFnw&index=1&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3 | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Cociente de potencias de la misma base | + | |titulo1=Tutorial 4b |
| |duracion=2'32" | |duracion=2'32" | ||
| - | |sinopsis=<math>a^n : a^m=a^{m-n}\;</math>. Ejemplos. | + | |sinopsis=Cociente de potencias de la misma base: <math>a^n : a^m=a^{m-n}\;</math>. Ejemplos. |
| |url1=https://www.youtube.com/watch?v=zUqq436AzxA&index=2&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3 | |url1=https://www.youtube.com/watch?v=zUqq436AzxA&index=2&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3 | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Potencia de exponente negativo | + | |titulo1=Tutorial 4c |
| - | |duracion=2'52" | + | |
| - | |sinopsis=<math>a^{-n} = \cfrac{1}{a^n}\;</math>. Ejemplos. | + | |
| - | |url1=https://www.youtube.com/watch?v=HCRNrY6htKs&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3&index=3 | + | |
| - | }} | + | |
| - | {{Video_enlace_virtual | + | |
| - | |titulo1=Potencia de exponente cero | + | |
| - | |duracion=1'35" | + | |
| - | |sinopsis=<math>a^0 = 1 \ , \ \forall a \ne 0\;</math>. Ejemplos. | + | |
| - | |url1=https://www.youtube.com/watch?v=2eGY2XDiz0E&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3&index=4 | + | |
| - | }} | + | |
| - | {{Video_enlace_virtual | + | |
| - | |titulo1=Potencia de otra potencia | + | |
| |duracion=1'58" | |duracion=1'58" | ||
| - | |sinopsis=<math>(a^n)^m = a^{n \cdot m}\;</math>. Ejemplos. | + | |sinopsis=Potencia de otra potencia: <math>(a^n)^m = a^{n \cdot m}\;</math>. Ejemplos. |
| |url1=https://www.youtube.com/watch?v=5QNCSxB2D6A&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3&index=5 | |url1=https://www.youtube.com/watch?v=5QNCSxB2D6A&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3&index=5 | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Potencia de un producto | + | |titulo1=Tutorial 4d |
| |duracion=2'48" | |duracion=2'48" | ||
| - | |sinopsis=<math>(a \cdot b)^n = a^n \cdot b^n\;</math>. Ejemplos. | + | |sinopsis=Potencia de un producto: <math>(a \cdot b)^n = a^n \cdot b^n\;</math>. Ejemplos. |
| |url1=https://www.youtube.com/watch?v=Ab5Mzr-whqM&index=6&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3 | |url1=https://www.youtube.com/watch?v=Ab5Mzr-whqM&index=6&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3 | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Potencia de un cociente | + | |titulo1=Tutorial 4e |
| |duracion=2'48" | |duracion=2'48" | ||
| - | |sinopsis=<math>\left( \cfrac{a}{b} \right)^n = \cfrac{a^n}{b^n}\;</math>. Ejemplos. | + | |sinopsis=Potencia de un cociente: <math>\left( \cfrac{a}{b} \right)^n = \cfrac{a^n}{b^n}\;</math>. Ejemplos. |
| |url1=https://www.youtube.com/watch?v=oAcdsF4fO94&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3&index=7 | |url1=https://www.youtube.com/watch?v=oAcdsF4fO94&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3&index=7 | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 5a | ||
| + | |duracion=8'12" | ||
| + | |sinopsis=*Potencias de exponente 1 y 0. | ||
| + | *Producto y cociente de potencias de la misma base. | ||
| + | *Potencia de un producto y de un cociente. | ||
| + | *Potencia de otra potencia. | ||
| + | *Ejemplos. | ||
| + | |url1=http://youtu.be/yc4-A5edFK0?list=PLwCiNw1sXMSCPdAlIxXUq7vq8c4wzj8To | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 5b | ||
| + | |duracion=6'26" | ||
| + | |sinopsis=*Potencias de base negativa. | ||
| + | *Potencias de exponente negativo. | ||
| + | *Ejemplos. | ||
| + | |url1=http://youtu.be/NFPibwNulnI?list=PLwCiNw1sXMSCPdAlIxXUq7vq8c4wzj8To | ||
| }} | }} | ||
| ---- | ---- | ||
| - | {{Video_enlace_clasematicas | + | {{Video_enlace_pildoras |
| - | |titulo1=Ejemplos de potencias de fracciones | + | |titulo1=Ejemplos 1 |
| - | |duracion=10'06" | + | |duracion=5'40" |
| - | |sinopsis=Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa. | + | |sinopsis=Cálculos con potencias de exponente positivo. |
| + | |url1=https://youtu.be/Ex1geRx9_Eg?list=PLwCiNw1sXMSCPdAlIxXUq7vq8c4wzj8To | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplos 2 | ||
| + | |duracion=3'35" | ||
| + | |sinopsis=Cálculos con potencias de exponente negativo. | ||
| + | |url1=https://youtu.be/CaOr3UK_xtg?list=PLwCiNw1sXMSCPdAlIxXUq7vq8c4wzj8To | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplos 3 | ||
| + | |duracion=6'55" | ||
| + | |sinopsis=Simplificaciones de operaciones con potencias. | ||
| + | |url1=https://youtu.be/kQFv3cEKtM8?list=PLwCiNw1sXMSCPdAlIxXUq7vq8c4wzj8To | ||
| + | }} | ||
| + | ---- | ||
| + | '''Cálculos con potencias de fracciones:''' | ||
| - | |url1=https://www.youtube.com/watch?v=MFqwHDRFj3k&list=PLZNmE9BEzVIlaXmK5LnHeDaCapzj-V198&index=4 | + | {{Video_enlace_escuela |
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=10'49" | ||
| + | |sinopsis=Calcula: | ||
| + | |||
| + | 20) <math>\left( \cfrac{-2~}{3} \right)^4 \cdot \left( \cfrac{-2~}{3} \right)^9</math> ; {{b4}}{{b4}} 21) <math>\left( \cfrac{-3~}{2} \right)^4 \cdot \left( \cfrac{-3~}{2} \right)^3</math> ; {{b4}}{{b4}} 22) <math>\left( \cfrac{3}{5} \right)^6 \cdot \left( \cfrac{3}{5} \right)^{-2}</math> | ||
| + | |||
| + | 23) <math>\left( \cfrac{1}{4} \right)^{-2} \cdot \left( \cfrac{1}{4} \right)^{-3}</math> ; {{b4}}{{b4}} 24) <math>\left( \cfrac{1}{4} \right)^5 \cdot \left( \cfrac{1}{4} \right)^{-3}</math> ; {{b4}}{{b4}} 25) <math>\left( \cfrac{2}{3} \right)^7 \cdot \left( \cfrac{2}{3} \right)^{-3}</math> | ||
| + | |||
| + | 26) <math>\left( \cfrac{-2~}{3} \right)^{-4} \cdot \left( \cfrac{-2~}{3} \right)^8</math> ; {{b4}}{{b4}} 27) <math>\left( \cfrac{2}{13} \right)^{-7} \cdot \left( \cfrac{2}{13} \right)^9</math> ; {{b4}}{{b4}} 28) <math>\left( \cfrac{1}{9} \right)^7 \cdot \left( \cfrac{1}{9} \right)^{-6}</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=6aC_gfAZE58&index=11&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY- | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=8'36" | ||
| + | |sinopsis=Calcula: | ||
| + | |||
| + | 29) <math>\left( \cfrac{3}{4} \right)^3 : \left( \cfrac{3}{4} \right)^2</math> ; {{b4}}{{b4}} 30) <math>\left( \cfrac{4}{3} \right)^{-2} : \left( \cfrac{4}{3} \right)^4</math> ; {{b4}}{{b4}} 31) <math>\left( \cfrac{3}{7} \right)^6 \cdot \left( \cfrac{3}{7} \right)^4</math> | ||
| + | |||
| + | 32) <math>\left( \cfrac{2}{5} \right)^{-2} : \left( \cfrac{2}{5} \right)^6</math> ; {{b4}}{{b4}} 33) <math>\left( \cfrac{-2~}{3} \right)^{-5} : \left( \cfrac{-2~}{3} \right)^{-3}</math> ; {{b4}}{{b4}} 34) <math>\left( \cfrac{-1~}{7} \right)^4 \cdot \left( \cfrac{-1~}{7} \right)^{-3}</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=PQWjTEzvjG4&index=12&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY- | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=10'26" | ||
| + | |sinopsis=Calcula: | ||
| + | |||
| + | :35) <math>\left[ \left( \cfrac{-3~}{7} \right)^2 \right]^3</math> ; {{b4}}{{b4}} 36) <math>\left[ \left( \cfrac{2}{3} \right)^3 \right]^5</math> ; {{b4}}{{b4}} 37) <math>\left[ \left( \cfrac{3}{4} \right)^2 \right]^4</math> | ||
| + | |||
| + | :38) <math>\left[ \left( \cfrac{2}{5} \right)^3 \right]^2</math> ; {{b4}}{{b4}} 39) <math>\left[ \left( \cfrac{2}{3} \right)^{-2} \right]^{-3}</math>; {{b4}}{{b4}} 40) <math>\left[ \left( \cfrac{3}{5} \right)^{-2} \right]^{-7}</math> | ||
| + | |||
| + | :41) <math>\left[ \left( \cfrac{-3~}{4} \right)^{-2} \right]^{-5}</math> ; {{b4}}{{b4}} 42) <math>\left[ \left( \cfrac{-2~}{7} \right)^3 \right]^{-2}</math> ; {{b4}}{{b4}} 43) <math>\left[ \left( \cfrac{-2~}{7} \right)^{-1} \right]^3</math> | ||
| + | |||
| + | :44) <math>\left[ \left( \cfrac{2}{5} \right)^{-3} \right]^{-2}</math> ; {{b4}}{{b4}} 45) <math>\left[ \left( \cfrac{-2~}{5} \right)^{-3} \right]^{-2}</math> ; {{b4}}{{b4}} 46) <math>\left[ \left( \cfrac{-1~}{8} \right)^{-2} \right]^{-3}</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=49qBtEWXgYU&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=13 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=5'28" | ||
| + | |sinopsis=Escribe como varias potencias: | ||
| + | |||
| + | :47) <math>\left( \cfrac{2}{3} \cdot \cfrac{1}{4} \cdot \cfrac{6}{5}\right)^2</math> | ||
| + | |||
| + | :48) <math>\left( \cfrac{1}{4} \cdot \cfrac{6}{25} \cdot \cfrac{5}{9}\right)^3</math> | ||
| + | |||
| + | :49) <math>\left( \cfrac{4}{5} \cdot \cfrac{5}{7} \cdot \cfrac{8}{6}\right)^3</math> | ||
| + | |||
| + | :50) <math>\left[ \cfrac{1}{3} \cdot \left( \cfrac{-2~}{5} \right) \cdot \left( \cfrac{-2~}{2} \right) \right]^2</math> | ||
| + | |||
| + | :51) <math>\left[ \cfrac{2}{3} \cdot \left( \cfrac{-5~}{4} \right) \cdot \cfrac{8}{5} \cdot \left( \cfrac{-5~}{2} \right) \right]^{-3}</math> | ||
| + | |url1=https://www.youtube.com/watch?v=Be6PSqNjvds&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=14 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=13'54" | ||
| + | |sinopsis=Escribe como una sola potencia: | ||
| + | |||
| + | :52) <math>\left( \cfrac{2}{5} \right)^2 \cdot \left( \cfrac{3}{7} \right)^2 \cdot \left( \cfrac{9}{11} \right)^2</math> | ||
| + | |||
| + | :53) <math>\left( \cfrac{1}{3} \right)^3 \cdot \left( \cfrac{1}{4} \right)^3 \cdot \left( \cfrac{5}{6} \right)^3</math> | ||
| + | |||
| + | :55) <math>\left( \cfrac{-2~}{3} \right)^2 \cdot \left( \cfrac{5}{4} \right)^2 \cdot \left( \cfrac{-3~}{5} \right)^2</math> | ||
| + | |||
| + | :56) <math>\left( \cfrac{-2~}{5} \right)^{-3} \cdot \left( \cfrac{1}{3} \right)^{-3} \cdot \left( \cfrac{5}{4} \right)^{-3}</math> | ||
| + | |||
| + | :57) <math>\left( \cfrac{-2~}{3} \right)^{-2} \cdot \left( \cfrac{1}{5} \right)^{-2} \cdot \left( \cfrac{3}{4} \right)^{-2}</math> | ||
| + | |||
| + | :58) <math>\left( \cfrac{2}{4} \right)^{-1} \cdot \left( \cfrac{-3~}{5} \right)^{-1} \cdot \left( \cfrac{5}{7} \right)^{-1}</math> | ||
| + | |||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=06M-dlh6tSw&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=15 | ||
| + | }} | ||
| + | |||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=9'43" | ||
| + | |sinopsis=Simplifica: | ||
| + | :a) <math>\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3</math> | ||
| + | |||
| + | :b) <math>\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2} </math> | ||
| + | |url1=https://www.youtube.com/watch?v=KdkMb7wSV4U | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=4'05" | ||
| + | |sinopsis=Simplifica <math>\cfrac{ \left(\cfrac{3}{4} \right)^5 \cdot \left(\cfrac{3}{4} \right)^{-2}}{ \left(\cfrac{3}{4} \right)^{-1} \cdot \left(\cfrac{3}{4} \right)^6}</math> | ||
| + | |url1=https://www.youtube.com/watch?v=mQiYuVeXZxM | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=2'08" | ||
| + | |sinopsis=Simplifica: <math>\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2 </math> | ||
| + | |url1=https://www.youtube.com/watch?v=yw1lx9htI2I | ||
| }} | }} | ||
| ---- | ---- | ||
| - | {{Video_enlace_tuprofesorvirtual | + | '''Cálculos con potencias dentro de fracciones:''' |
| + | |||
| + | {{Video_enlace_escuela | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| - | |duracion=2'09" | + | |duracion=10'23" |
| - | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>2 a^3 \cdot a^5</math>}} | + | |sinopsis=Calcula: |
| - | |url1=https://www.youtube.com/watch?v=3MdP1Wxbj8Y&list=PLTDunuLIi6ogbD4_joialQfNyKekQcbnG&index=19 | + | |
| + | :59) <math>\cfrac{3^2 \cdot 3^3 \cdot 3}{3^4}\;</math> | ||
| + | |||
| + | :60) <math>\cfrac{4^{-1} \cdot 4^{-3}}{4^{-2} \cdot 4^{-5}}\;</math> | ||
| + | |||
| + | :61) <math>\cfrac{2 \cdot 2^{-3}}{2^{-2}}\;</math> | ||
| + | |||
| + | :62) <math>\cfrac{(-2)^{-3} \cdot (-2)^5 \cdot (-2)}{(-2)^{-1} \cdot (-2)^3}\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=dhd1kiF-oPg&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=16 | ||
| }} | }} | ||
| - | {{Video_enlace_tuprofesorvirtual | + | {{Video_enlace_escuela |
| |titulo1=Ejercicio 2 | |titulo1=Ejercicio 2 | ||
| + | |duracion=7'23" | ||
| + | |sinopsis=Calcula: | ||
| + | |||
| + | :63) <math>\cfrac{2^2 \cdot 2^{-3} \cdot 2^5}{2^4 \cdot 2^{-1}}\;</math> | ||
| + | |||
| + | :64) <math>\cfrac{6^{-1} \cdot (6^5)^2}{6^2 \cdot 6^3}\;</math> | ||
| + | |||
| + | :65) <math>\cfrac{4^{-1} \cdot 4^{-3}}{4^{-2} \cdot 4^{-4}}\;</math> | ||
| + | |||
| + | :66) <math>\cfrac{(-3)^{-2} \cdot (-3)^{-3}}{\left[ (-3)^2 \right]^{-2}}\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=Tojm9kQ1FjU&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=17 | ||
| + | }} | ||
| + | {{Video_enlace_tuprofesorvirtual | ||
| + | |titulo1=Ejercicio 3 | ||
| |duracion=3'37" | |duracion=3'37" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left( \cfrac{5 \cdot 4 \cdot 3}{6 \cdot 2} \right)^2</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left( \cfrac{5 \cdot 4 \cdot 3}{6 \cdot 2} \right)^2</math>}} | ||
| Línea 81: | Línea 248: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 3 | + | |titulo1=Ejercicio 4 |
| |duracion=3'42" | |duracion=3'42" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3</math>}} | ||
| Línea 87: | Línea 254: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 4 | + | |titulo1=Ejercicio 5 |
| |duracion=3'40" | |duracion=3'40" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{(3x^2y)^5}{3x^4y^7}</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{(3x^2y)^5}{3x^4y^7}</math>}} | ||
| Línea 93: | Línea 260: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 5 | + | |titulo1=Ejercicio 6 |
| |duracion=2'47" | |duracion=2'47" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{2^{16}}{2^{13}}+\cfrac{5^3 \cdot 3^8}{5^2 \cdot 3^6}</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{2^{16}}{2^{13}}+\cfrac{5^3 \cdot 3^8}{5^2 \cdot 3^6}</math>}} | ||
| Línea 99: | Línea 266: | ||
| }} | }} | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Ejercicio 6 | + | |titulo1=Ejercicio 7 |
| |duracion=17'31" | |duracion=17'31" | ||
| |sinopsis=Simplifica y expresa la solución como una única potencia: | |sinopsis=Simplifica y expresa la solución como una única potencia: | ||
| Línea 115: | Línea 282: | ||
| }} | }} | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Ejercicio 7 | + | |titulo1=Ejercicio 8 |
| |duracion=14'41" | |duracion=14'41" | ||
| |sinopsis=Simplifica y expresa la solución como una única potencia: | |sinopsis=Simplifica y expresa la solución como una única potencia: | ||
| Línea 133: | Línea 300: | ||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Ejercicio 8 | + | |titulo1=Ejercicio 9 |
| |duracion=11'39" | |duracion=11'39" | ||
| |sinopsis=Simplifica: | |sinopsis=Simplifica: | ||
| Línea 139: | Línea 306: | ||
| :b)<math>\cfrac{15^6 \cdot 12^4}{10^5 \cdot 3^6 \cdot 81}</math> | :b)<math>\cfrac{15^6 \cdot 12^4}{10^5 \cdot 3^6 \cdot 81}</math> | ||
| |url1=https://www.youtube.com/watch?v=qu7wc8f1wVs | |url1=https://www.youtube.com/watch?v=qu7wc8f1wVs | ||
| - | }} | ||
| - | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejercicio 9 | ||
| - | |duracion=9'43" | ||
| - | |sinopsis=Simplifica: | ||
| - | :a) <math>\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3</math> | ||
| - | |||
| - | :b) <math>\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2} </math> | ||
| - | |url1=https://www.youtube.com/watch?v=KdkMb7wSV4U | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| |titulo1=Ejercicio 10 | |titulo1=Ejercicio 10 | ||
| - | |duracion=4'05" | ||
| - | |sinopsis=Simplifica <math>\cfrac{ \left(\cfrac{3}{4} \right)^5 \cdot \left(\cfrac{3}{4} \right)^{-2}}{ \left(\cfrac{3}{4} \right)^{-1} \cdot \left(\cfrac{3}{4} \right)^6}</math> | ||
| - | |url1=https://www.youtube.com/watch?v=mQiYuVeXZxM | ||
| - | }} | ||
| - | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 11 | ||
| |duracion=13'13" | |duracion=13'13" | ||
| |sinopsis=Simplifica: | |sinopsis=Simplifica: | ||
| Línea 166: | Línea 318: | ||
| |url1=https://www.youtube.com/watch?v=rhfNNh-alBI | |url1=https://www.youtube.com/watch?v=rhfNNh-alBI | ||
| }} | }} | ||
| - | {{Video_enlace_julioprofe | + | ---- |
| - | |titulo1=Ejercicio 12 | + | '''Cálculos de diversos tipos:''' |
| - | |duracion=2'08" | + | |
| - | |sinopsis=Simplifica: <math>\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2 </math> | + | |
| - | |url1=https://www.youtube.com/watch?v=yw1lx9htI2I | + | |
| - | }} | + | |
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=10'06" | ||
| + | |sinopsis=Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa. | ||
| + | |||
| + | '''Exponente positivo:''' | ||
| + | |||
| + | :a) <math>\left( \cfrac{2}{5} \right)^3</math> ; {{b4}}{{b4}}b) <math>\left( \cfrac{-3}{7} \right)^2</math> ; {{b4}}{{b4}}c) <math>\left( \cfrac{-5}{3} \right)^3</math> ; {{b4}}{{b4}}d) <math>\cfrac{4^3}{3}</math> ; {{b4}}{{b4}}e) <math>-\cfrac{5^2}{8}</math> | ||
| + | ---- | ||
| + | '''Exponente negativo:''' | ||
| + | |||
| + | :f) <math>\left( \cfrac{2}{5} \right)^{-3}</math> ; {{b4}}{{b4}}g) <math>\left( -\cfrac{3}{7} \right)^{-2}</math> ; {{b4}}{{b4}}h) <math>\left( \cfrac{-5}{3} \right)^{-3}</math> ; {{b4}}{{b4}}i) <math>4^{-3}\;</math> ; {{b4}}{{b4}}j) <math>-\cfrac{2^{-3}}{3}</math> | ||
| + | ---- | ||
| + | '''Operaciones combinadas:''' | ||
| + | |||
| + | :k) <math>\cfrac{5^2}{3} \cdot \left( \cfrac{4}{18} \right)^{-1} : 5</math> ; {{b4}}{{b4}}l) <math>\cfrac{6}{10} \cdot \left( \cfrac{3}{5} \right)^{-2} : \left( \cfrac{5}{2} \right)^2 \cdot 2^{-1}</math> | ||
| + | |url1=https://www.youtube.com/watch?v=MFqwHDRFj3k&list=PLZNmE9BEzVIlaXmK5LnHeDaCapzj-V198&index=4 | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
Tutorial muy completo que explica las propiedades básicas de las potencias con ejemplos resueltos sencillos y alguno más complejo.
- Potencias de exponente entero de números racionales.
- Propiedades.
- Ejemplos
Producto de potencias de fracciones con la misma base. Ejemplos.
Cociente de potencias de fracciones con la misma base. Ejemplos.
Potencia de otra potencia de una fracción. Ejemplos.
Potencia de un producto de fracciones. Ejemplos.
Producto de potencias de la misma base: 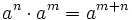 . Ejemplos.
. Ejemplos.
Cociente de potencias de la misma base: 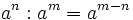 . Ejemplos.
. Ejemplos.
Potencia de otra potencia: 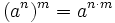 . Ejemplos.
. Ejemplos.
Potencia de un producto: 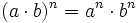 . Ejemplos.
. Ejemplos.
Potencia de un cociente: 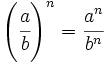 . Ejemplos.
. Ejemplos.
- Potencias de exponente 1 y 0.
- Producto y cociente de potencias de la misma base.
- Potencia de un producto y de un cociente.
- Potencia de otra potencia.
- Ejemplos.
- Potencias de base negativa.
- Potencias de exponente negativo.
- Ejemplos.
Cálculos con potencias de exponente positivo.
Cálculos con potencias de exponente negativo.
Simplificaciones de operaciones con potencias.
Cálculos con potencias de fracciones:
Calcula:
20) 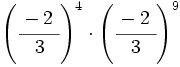 ; 21)
; 21) 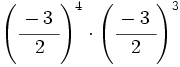 ; 22)
; 22) 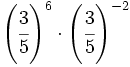
23) 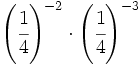 ; 24)
; 24) 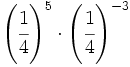 ; 25)
; 25) 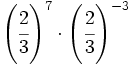
26)  ; 27)
; 27) 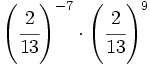 ; 28)
; 28) 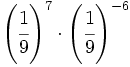
Calcula:
29) 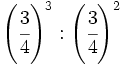 ; 30)
; 30)  ; 31)
; 31) 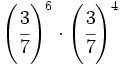
32) 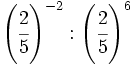 ; 33)
; 33) 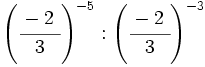 ; 34)
; 34) 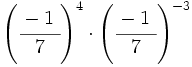
Calcula:
- 35)
![\left[ \left( \cfrac{-3~}{7} \right)^2 \right]^3](/wikipedia/images/math/0/d/5/0d5ecdfc87205ac8f368d6a70a5e1225.png) ; 36)
; 36) ![\left[ \left( \cfrac{2}{3} \right)^3 \right]^5](/wikipedia/images/math/2/9/c/29cf02b990eee91e9f5267cd7ae27ab8.png) ; 37)
; 37) ![\left[ \left( \cfrac{3}{4} \right)^2 \right]^4](/wikipedia/images/math/8/5/9/85905a10045ecdadf0d87cb496b46fd4.png)
- 38)
![\left[ \left( \cfrac{2}{5} \right)^3 \right]^2](/wikipedia/images/math/7/7/c/77ccd9469ab61459b42b5c42c31b6a03.png) ; 39)
; 39) ![\left[ \left( \cfrac{2}{3} \right)^{-2} \right]^{-3}](/wikipedia/images/math/7/1/7/717d66168670db7c17604eed1ecc5697.png) ; 40)
; 40) ![\left[ \left( \cfrac{3}{5} \right)^{-2} \right]^{-7}](/wikipedia/images/math/7/d/5/7d5523f771792c7a7444cc796d7a29e6.png)
- 41)
![\left[ \left( \cfrac{-3~}{4} \right)^{-2} \right]^{-5}](/wikipedia/images/math/d/e/2/de20c03afc7ad82625777cdcf282c409.png) ; 42)
; 42) ![\left[ \left( \cfrac{-2~}{7} \right)^3 \right]^{-2}](/wikipedia/images/math/d/8/f/d8f17a4b8bd520d1104f16e3bbe69742.png) ; 43)
; 43) ![\left[ \left( \cfrac{-2~}{7} \right)^{-1} \right]^3](/wikipedia/images/math/d/9/9/d996341203e6a65e266433c712564961.png)
- 44)
![\left[ \left( \cfrac{2}{5} \right)^{-3} \right]^{-2}](/wikipedia/images/math/e/2/b/e2b4f1793a567fb108f0a0c11c815bcb.png) ; 45)
; 45) ![\left[ \left( \cfrac{-2~}{5} \right)^{-3} \right]^{-2}](/wikipedia/images/math/1/5/4/154452bc7b4e3830e7474ee197167695.png) ; 46)
; 46) ![\left[ \left( \cfrac{-1~}{8} \right)^{-2} \right]^{-3}](/wikipedia/images/math/d/f/7/df755b98eccd3553b490053829676d47.png)
Escribe como varias potencias:
- 47)
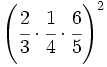
- 48)
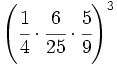
- 49)
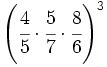
- 50)
![\left[ \cfrac{1}{3} \cdot \left( \cfrac{-2~}{5} \right) \cdot \left( \cfrac{-2~}{2} \right) \right]^2](/wikipedia/images/math/5/b/1/5b1a30cdfd3990559ce215699a00c2e3.png)
- 51)
![\left[ \cfrac{2}{3} \cdot \left( \cfrac{-5~}{4} \right) \cdot \cfrac{8}{5} \cdot \left( \cfrac{-5~}{2} \right) \right]^{-3}](/wikipedia/images/math/4/0/6/4066e6d3414c3e8d17a4b0e6837cad6a.png)
Escribe como una sola potencia:
- 52)
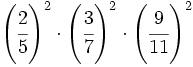
- 53)
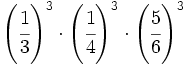
- 55)
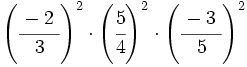
- 56)
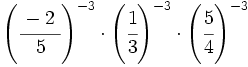
- 57)
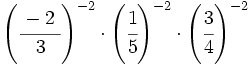
- 58)
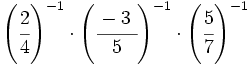
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 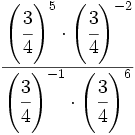
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Cálculos con potencias dentro de fracciones:
Calcula:
- 59)
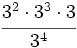
- 60)
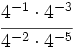
- 61)
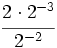
- 62)
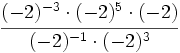
Calcula:
- 63)
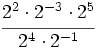
- 64)
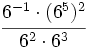
- 65)
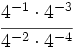
- 66)
![\cfrac{(-3)^{-2} \cdot (-3)^{-3}}{\left[ (-3)^2 \right]^{-2}}\;](/wikipedia/images/math/5/e/b/5eb0dbb75ab3ac5de8238f112e4d893f.png)
Simplifica: 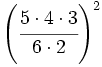
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 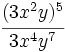
Simplifica: 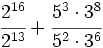
Simplifica y expresa la solución como una única potencia:
a) 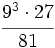
b) 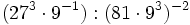
c) 
d) 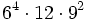
e) a) 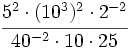
Simplifica y expresa la solución como una única potencia:
a) 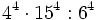
b) 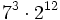
c) 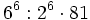
d) 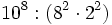
e) 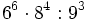
f) 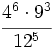
Simplifica:
- a)
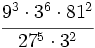
- b)
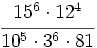
Simplifica:
- a)
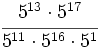
- b)
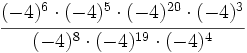
- c)
![\left[ \cfrac{( 2^3 \cdot 2^6)^{-2} \cdot (3^4)^3 \cdot 3 }{( 2^6 \cdot 2^{10})^{-1}\cdot (3^6 \cdot 3^2 \cdot 3^5)}\right]^{10}](/wikipedia/images/math/c/8/5/c85c926802bdbb7a51ef34eb65c6dda7.png)
Cálculos de diversos tipos:
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Exponente positivo:
- a)
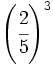 ; b)
; b)  ; c)
; c)  ; d)
; d) 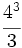 ; e)
; e) 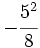
Exponente negativo:
- f)
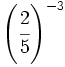 ; g)
; g) 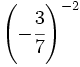 ; h)
; h) 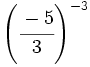 ; i)
; i) 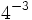 ; j)
; j) 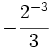
Operaciones combinadas:
- k)
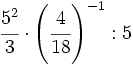 ; l)
; l)