Plantilla:Def Multiplo y divisor
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 15:55 13 sep 2019 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 15:56 13 sep 2019 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| |demo=En efecto, si ''a'' es multiplo de ''b'', entonces la división ''a:b'' es exacta. Si llamamos ''k'' al cociente, se cumple que a=b·k.}} | |demo=En efecto, si ''a'' es multiplo de ''b'', entonces la división ''a:b'' es exacta. Si llamamos ''k'' al cociente, se cumple que a=b·k.}} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Los números naturales|enunciado= | + | {{Videotutoriales|titulo=Múltiplos y divisores|enunciado= |
| - | {{Video_enlace_pildoras | + | |
| - | |titulo1=Tutorial 1 | + | |
| - | |duracion=5'03" | + | |
| - | |sinopsis=Múltiplos y divisores de un número. Ejemplos. | + | |
| - | |url1=https://youtu.be/OCHa6bYAdDU?list=PLwCiNw1sXMSBRdXXWmrBi1gHHpFDeppJE | + | |
| - | }} | + | |
| {{Video_enlace_miguematicas | {{Video_enlace_miguematicas | ||
| - | |titulo1=Tutorial 2 | + | |titulo1=Tutorial 1 |
| |duracion=2'05" | |duracion=2'05" | ||
| |sinopsis=¿Cómo se sabe si un número es múltiplo o divisor? | |sinopsis=¿Cómo se sabe si un número es múltiplo o divisor? | ||
| |url1=https://www.youtube.com/watch?v=xlySLPZA4tc | |url1=https://www.youtube.com/watch?v=xlySLPZA4tc | ||
| }} | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=5'03" | ||
| + | |sinopsis=Múltiplos y divisores de un número. Ejemplos. | ||
| + | |url1=https://youtu.be/OCHa6bYAdDU?list=PLwCiNw1sXMSBRdXXWmrBi1gHHpFDeppJE | ||
| + | }} | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 15:56 13 sep 2019
Si 
y 
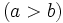están emparentados por la relación de divisibilidad, es decir, 
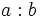es exacta, entonces decimos que:
- es multiplo y lo expresaremos simbólicamente: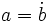
.
- es divisor de y lo expresaremos simbólicamente: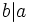
.
- La división 60:15=4 es exacta. Entonces 60 es un múltiplo de 15
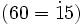y 15 es un divisor de 60 
.
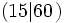- Fíjate que 4 también es divisor de 60 porque la división 60:4=15 es también exacta. Por tanto, los divisores siempre van por parejas.
Proposición
Si es multiplo de , entonces existe un número entero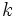 
tal que 
.
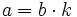Demostración:
En efecto, si a es multiplo de b, entonces la división a:b es exacta. Si llamamos k al cociente, se cumple que a=b·k.
Tutorial 1 (2'05") Sinopsis:¿Cómo se sabe si un número es múltiplo o divisor?
Tutorial 2 (5'03") Sinopsis:Múltiplos y divisores de un número. Ejemplos.
Las definiciones vistas hasta ahora las podríamos haber dado igualmente cambiando números enteros por números naturales. En lo que resta de tema sólo hablaremos de números naturales para evitar duplicidades por cuestiones de signo, sin embargo, todo lo que digamos será también aplicable a números enteros, salvo pequeños matices que obviaremos por cuestiones de simplicidad.
Propiedades
Propiedades de los múltiplos
- Todo número natural es múltiplo de 1 y de sí mismo.
- Todo número natural
tiene infinitos múltiplos,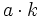 
, que se obtienen multiplicándolo por un número natural 
cualquiera.
- El 0 es múltiplo de cualquier número.
- La suma de dos o más multiplos de es otro múltiplo de .
- La diferencia de dos múltiplos de un número es otro múltiplo de dicho número.
- Si un número es múltiplo de otro, y éste lo es de un tercero, el primero es múltiplo del tercero.
- Si un número es múltiplo de otro, todos los múltiplos del primero lo son también del segundo.
Propiedades de los divisores
- Todo número natural distinto de cero tiene al menos dos divisores: 1 y él mismo.
- Todo divisor de un número distinto de cero es menor o igual a él. Por tanto, el número de divisores es finito.
- Si un número es divisor de otros dos, también lo es de su suma y de su diferencia.
- Si un número es divisor de otro, también lo es de cualquier múltiplo de éste.
- Si un número es divisor de otro, y éste lo es de un tercero, el primero lo es del tercero.
