Ángulo entre dos rectas del plano (1ºBach)
De Wikipedia
| Revisión de 18:45 29 jul 2017 Coordinador (Discusión | contribuciones) (→Ángulo entre dos rectas a partir de sus pendientes) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ángulo entre dos rectas a partir de sus pendientes) |
||
| Línea 53: | Línea 53: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Ángulo entre dos rectas|enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=6´06" | ||
| + | |url1=https://youtu.be/040aVzsO5N0?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| + | |sinopsis=Cálculo del ángulo entre dos rectas. Ejemplos. | ||
| + | |||
| + | '''Nota:''' En este tutorial se usa la fórmula sin valor absoluto, con lo cual en unos casos sale el ángulo mayor y en otros el menor. | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicio | ||
| + | |duracion=6´46" | ||
| + | |url1=https://youtu.be/8VDYIxWr_mA?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| + | |sinopsis=Cálculo de los ángulos de un triángulo conocidas las coordenadas de los vértices. | ||
| + | }} | ||
| + | }} | ||
| ==Ángulo entre dos rectas dadas en forma implícita== | ==Ángulo entre dos rectas dadas en forma implícita== | ||
| Línea 67: | Línea 83: | ||
| <center><math>tg \, \phi = \Big| \cfrac{m'-m}{1+m \,m'} \Big|</math></center> | <center><math>tg \, \phi = \Big| \cfrac{m'-m}{1+m \,m'} \Big|</math></center> | ||
| + | |||
| |demo={{Tabla75|celda2=[[Imagen:ang2rectas.png]]|celda1= | |demo={{Tabla75|celda2=[[Imagen:ang2rectas.png]]|celda1= | ||
| Teniendo en cuenta que <math>m=tg \, \alpha</math> y <math>m'=tg \, \beta</math>, usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos: | Teniendo en cuenta que <math>m=tg \, \alpha</math> y <math>m'=tg \, \beta</math>, usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos: | ||
| - | :<math>tg \, \phi=tg \, (\alpha - \beta)= \Big| \cfrac{tg \, \alpha - tg \, \beta}{1+tg \, \alpha \, tg \, \beta} \Big|= \Big| \cfrac{m'-m}{1+m \,m'} \Big|</math> | + | <center><math>tg \, \phi=tg \, (\alpha - \beta)= \cfrac{tg \, \alpha - tg \, \beta}{1+tg \, \alpha \, tg \, \beta} = \cfrac{m'-m}{1+m \,m'} </math></center> |
| + | |||
| + | Para conseguir que el ángulo sea el menor, tomamos valores absolutos en la expresión anterior: | ||
| + | |||
| + | <center><math>tg \, \phi=\Big| \cfrac{m'-m}{1+m \,m'} \Big|</math></center> | ||
| + | |||
| + | {{p}} | ||
| ---- | ---- | ||
| También puedes ver la demostración en el siguiente video: | También puedes ver la demostración en el siguiente video: | ||
| Línea 83: | Línea 106: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Video_enlace_velazco | ||
| + | |titulo1=Ejemplo | ||
| + | |duracion=8´41" | ||
| + | |url1=https://www.youtube.com/watch?v=PiVwCSU9VyE&list=PLPrT9FThiZ6QfKolkw-a6qholvFwVde1n&index=9 | ||
| + | |sinopsis=Halla el ángulo entre las rectas <math>r_1: -x+y=2\;</math> {{b}} y {{b}} <math>r_2: -5x-4y=13\;</math>. | ||
| + | }} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás calcular el ángulo entre dos rectas. | |descripcion=En esta escena podrás calcular el ángulo entre dos rectas. | ||
| Línea 91: | Línea 120: | ||
| ==Ejercicios y videotutoriales== | ==Ejercicios y videotutoriales== | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Ángulo entre dos rectas. Paralelismo y perpendicularidad|enunciado= | + | {{Videotutoriales|titulo=Ángulo entre dos rectas|enunciado= |
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1=Tutorial | |titulo1=Tutorial | ||
| Línea 118: | Línea 147: | ||
| |url1=https://www.youtube.com/watch?v=jI_UhPEnXMI&list=PLF10C7CAD9DEE955C&index=13 | |url1=https://www.youtube.com/watch?v=jI_UhPEnXMI&list=PLF10C7CAD9DEE955C&index=13 | ||
| |sinopsis=Ángulo entre dos rectas | |sinopsis=Ángulo entre dos rectas | ||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 4 | ||
| - | |duracion=10´22" | ||
| - | |url1=https://www.youtube.com/watch?v=7jGWTzKyo2g&list=PLF10C7CAD9DEE955C&index=14 | ||
| - | |sinopsis=3 ejercicios (Paralelismo) | ||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 5 | ||
| - | |duracion=9´44" | ||
| - | |url1=https://www.youtube.com/watch?v=vFE3NKgSCvU&list=PLF10C7CAD9DEE955C&index=15 | ||
| - | |sinopsis=3 ejercicios (Perpendicularidad) | ||
| - | |||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 6 | ||
| - | |duracion=6´12" | ||
| - | |url1=https://www.youtube.com/watch?v=RY0ar7IIM9I&list=PLF10C7CAD9DEE955C&index=16 | ||
| - | |sinopsis=2 ejercicios (Perpendicularidad) | ||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 7 | ||
| - | |duracion=7´20" | ||
| - | |url1=https://www.youtube.com/watch?v=KNqpqXu6-gg&list=PLF10C7CAD9DEE955C&index=17 | ||
| - | |sinopsis=Ejercicio (Simétrico de un punto respecto a una recta) | ||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 8 | ||
| - | |duracion=8´11" | ||
| - | |url1=https://www.youtube.com/watch?v=sZcqcnGaLsI&list=PLF10C7CAD9DEE955C&index=18 | ||
| - | |sinopsis=Ejercicio (Ortocentro de un triángulo) | ||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 9 | ||
| - | |duracion=11'24" | ||
| - | |url1=https://www.youtube.com/watch?v=KupShRsfM48&list=PLF10C7CAD9DEE955C&index=19 | ||
| - | |sinopsis=Ejercicio (Circuncentro de un triángulo) | ||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 10 | ||
| - | |duracion=6'38" | ||
| - | |url1=https://www.youtube.com/watch?v=d74xcLxkJnA&list=PLF10C7CAD9DEE955C&index=20 | ||
| - | |sinopsis=Ejercicio (Triángulo equilátero) | ||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 11 | ||
| - | |duracion=4'36" | ||
| - | |url1=https://www.youtube.com/watch?v=N8uvuaggBOU&list=PLF10C7CAD9DEE955C&index=21 | ||
| - | |sinopsis=Ejercicio (Triángulo isósceles) | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 202)
Ángulo entre dos rectas
El ángulo entre dos rectas del plano es el menor de los dos ángulos que forman éstas entre sí.
Ángulo entre dos rectas a partir de sus vectores de dirección
Ejemplo: Ángulo entre dos rectas
Halla el ángulo que forman las siguientes rectas:
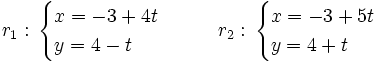
Sus vectores de dirección son: 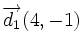 y
y 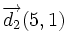 , de manera que:
, de manera que:
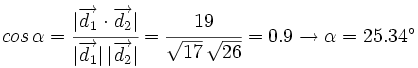
Cálculo del ángulo entre dos rectas. Ejemplos.
Nota: En este tutorial se usa la fórmula sin valor absoluto, con lo cual en unos casos sale el ángulo mayor y en otros el menor.
Cálculo de los ángulos de un triángulo conocidas las coordenadas de los vértices.
Ángulo entre dos rectas dadas en forma implícita
Proposición
Sean 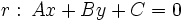 y
y 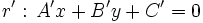 dos rectas, y sea
dos rectas, y sea  el ángulo que forman. Se verifica que
el ángulo que forman. Se verifica que
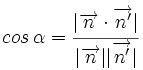
- donde
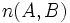 y
y 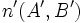 son los vectores normales de las rectas.
son los vectores normales de las rectas.
Cómo el vector normal a una recta es perpendicular al vector de dirección de la misma, hallar el ángulo entre las dos rectas equivale a hallar el ángulo entre los vectores normales o entre los vectores de dirección. Por tanto aplicaremos la misma fórmula que para hallar el ángulo a partir de los vectores de dirección, sustituyendo éstos por los vectores normales.
Ángulo entre dos rectas a partir de sus pendientes
Proposición
Dadas dos rectas con pendientes  y
y 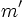 . Se verifica que
. Se verifica que
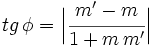
Teniendo en cuenta que 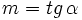 y y 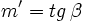 , usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos: , usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos:
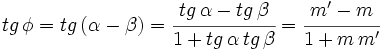 Para conseguir que el ángulo sea el menor, tomamos valores absolutos en la expresión anterior: 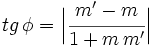 También puedes ver la demostración en el siguiente video: Demostración de la fórmula del ángulo entre dos rectas conocidas sus pendientes. | 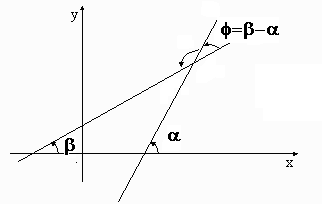
|
Halla el ángulo entre las rectas 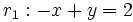 y
y 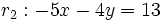 .
.
En esta escena podrás calcular el ángulo entre dos rectas.
Ejercicios y videotutoriales
- Ángulo entre dos rectas.
- Paralelismo y perpendicularidad.
Ángulo entre dos rectas
Ángulo entre dos rectas
Ángulo entre dos rectas
Ejercicios propuestos
|
Ejercicios propuestos: Ecuaciones trigonométricas |
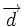
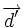
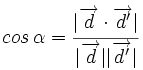
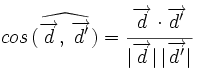
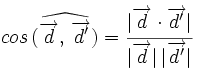
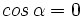 , de donde
, de donde 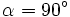 .
.