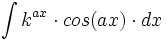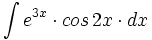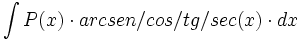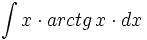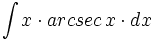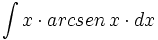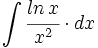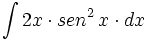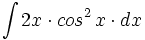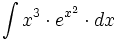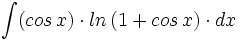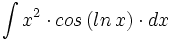Cálculo de primitivas por partes (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:31 15 sep 2019 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:34 15 sep 2019 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 51: | Línea 51: | ||
| #<math>\int e^x(x^2-3) \cdot dx</math> | #<math>\int e^x(x^2-3) \cdot dx</math> | ||
| |url1=https://youtu.be/Ac3H12gln6c?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | |url1=https://youtu.be/Ac3H12gln6c?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplos 3 | ||
| + | |duracion=10'21" | ||
| + | |sinopsis=Integración por partes cíclica: | ||
| + | #<math>\int e^x \cdot sen\,x \cdot dx</math> | ||
| + | #<math>\int sen(ln\,x) \cdot dx</math> | ||
| + | |url1=https://youtu.be/Q-Io234FjwM?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 16:34 15 sep 2019
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Fórmula de la integración por partes. Regla mnemotécnica. Ejemplo.
Integración por partes. Regla mnemotécnica para la selección de las funciones. Ejemplo.
- Deducción de la fórmula de integración "por partes".
- Casos típicos de aplicación.
Integración por partes en varios pasos:
Integración por partes cíclica:
Ejercicios resueltos: Cálculo de primitivas por partes
Primitivas del tipo 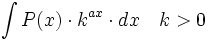 donde
donde  es un polinomio.
es un polinomio.
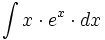
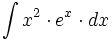
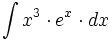
- Determina las infinitas funciones cuya segunda derivada es
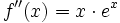 , obteniendo la que pasa por los puntos (0,2) y (2,0).
, obteniendo la que pasa por los puntos (0,2) y (2,0).
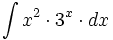
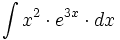
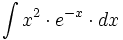
Ejemplos: Cálculo de primitivas por partes
Ejemplos: Cálculo de primitivas por partes
Primitivas del tipo 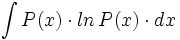
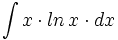
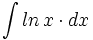
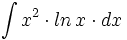
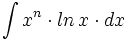
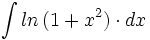
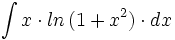
- Determina la primitiva de
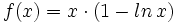 que pasa por el punto (1,1).
que pasa por el punto (1,1).
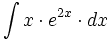
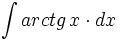
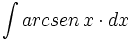
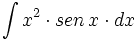
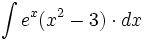
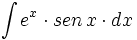
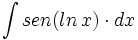
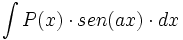 ó
ó 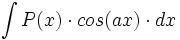 donde
donde 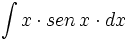
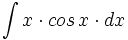
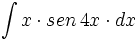
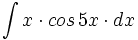
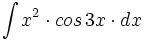
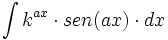 ó
ó