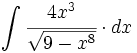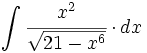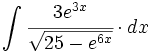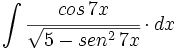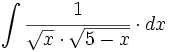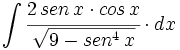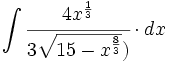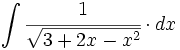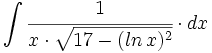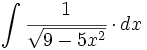Cálculo de primitivas inmediatas (2ºBach)
De Wikipedia
| Revisión de 18:05 31 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace2 | + | __TOC__ |
| - | |titulo1=Primitivas inmediatas | + | ==Integrales inmediatas básicas== |
| - | |duracion='" | + | Empezaremos viendo aquellas funciones cuyas primitivas son las funciones elementales. Basta con recordar las reglas de derivación que vimos en un tema anterior y que puedes ver en el siguiente enlace: [[Reglas de derivación (2ºBach)|'''Ver reglas de derivación''']]. |
| + | |||
| + | {{Videotutoriales|titulo=Integrales básicas|enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1a | ||
| + | |duracion=7'25" | ||
| + | |sinopsis=Reglas básicas de integración: | ||
| + | |||
| + | *Integral de un número. | ||
| + | *Integral de una potencia. | ||
| + | |url1=https://youtu.be/Mw8CiYjSYkw?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1b | ||
| + | |duracion=8'50" | ||
| + | |sinopsis=Reglas básicas de integración: | ||
| + | |||
| + | *Integral de una potencia (ampliación). | ||
| + | *Integral del logaritmo neperiano. | ||
| + | |url1=https://youtu.be/P4jLkgSUAzo?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1c | ||
| + | |duracion=6'48" | ||
| + | |sinopsis=Reglas básicas de integración: | ||
| + | |||
| + | *Integral de funciones exponenciales. | ||
| + | |url1=https://youtu.be/qDKB2qks1gY?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1d | ||
| + | |duracion=5'27" | ||
| + | |sinopsis=Reglas básicas de integración: | ||
| + | |||
| + | *Integral de funciones trigonométricas. | ||
| + | |url1=https://youtu.be/fij8SF5AMW8?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1e | ||
| + | |duracion=7'24" | ||
| + | |sinopsis=Reglas básicas de integración: | ||
| + | |||
| + | *Integral de funciones trigonométricas (ampliación). | ||
| + | |url1=https://youtu.be/a8h0EUAUf9o?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | ==Integrales inmediatas== | ||
| + | En este apartado estudiaremos las integrales de funciones cuyas primitivas son funciones compuestas. Más concretamente: | ||
| + | {{p}} | ||
| + | {{Teorema|titulo=Proposición|enunciado= | ||
| + | :<math>\int g'[f(x)] \cdot f'(x) \, dx = g[f(x)] + k </math> | ||
| + | |demo= | ||
| + | '''Demostración:''' | ||
| + | |||
| + | Es inmediato si a partir de la derivada de la función compuesta | ||
| + | |||
| + | :<math>(g[f(x)])'= g[f(x)] \cdot f'(x)</math> | ||
| + | |||
| + | integramos ambos miembros. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Integrales inmediatas|enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1a | ||
| + | |duracion=7'57" | ||
| + | |sinopsis=Integrales inmediatas. | ||
| + | |url1=https://youtu.be/ihgb7gtyQhY?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1b | ||
| + | |duracion=9'31" | ||
| + | |sinopsis=Integrales inmediatas (continuación). | ||
| + | |url1=https://youtu.be/VyfkQt4z_NE?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1c | ||
| + | |duracion=9'49" | ||
| + | |sinopsis=Integrales inmediatas (continuación). | ||
| + | |url1=https://youtu.be/srMqFO99fYQ?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=5'31" | ||
| + | |sinopsis=Integrales inmediatas | ||
| + | |url1=https://www.youtube.com/watch?v=Tq1_RI4He6g&index=4&list=PLECA0C7A8B59E5534 | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplos 1 | ||
| + | |duracion=10'22" | ||
| |sinopsis= | |sinopsis= | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/01/in01_05.html | + | #<math>\int x^2-5x+9 \cdot dx</math> |
| + | #<math>\int \cfrac{1}{x^3}+\cfrac{7}{x^2} \cdot dx</math> | ||
| + | #<math>\int \sqrt[4]{x} \cdot dx</math> | ||
| + | #<math>\int 2(2x-8)^6 \cdot dx</math> | ||
| + | #<math>\int x(x^2-8)^3 \cdot dx</math> | ||
| + | #<math>\int \cfrac{x^2}{(x^3+5)^4} \cdot dx</math> | ||
| + | #<math>\int \cfrac{3}{\sqrt{5x}} \cdot dx</math> | ||
| + | |url1=https://youtu.be/H2ghV-JaUgk?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplos 2 | ||
| + | |duracion=10'14" | ||
| + | |sinopsis= | ||
| + | #<math>\int e^{-6x} \cdot dx</math> | ||
| + | #<math>\int e^{\cfrac{3x}{2}} \cdot dx</math> | ||
| + | #<math>\int 3x \cdot e^{x^2} \cdot dx</math> | ||
| + | #<math>\int 4^x \cdot ln\,4 \cdot dx</math> | ||
| + | #<math>\int 4^x \cdot dx</math> | ||
| + | #<math>\int 5^{7x} \cdot dx</math> | ||
| + | |||
| + | |url1=https://youtu.be/axA6MMKsK-c?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplos 3 | ||
| + | |duracion=8'36" | ||
| + | |sinopsis= | ||
| + | #<math>\int \cfrac{2x}{x^2+3} \cdot dx</math> | ||
| + | #<math>\int \cfrac{x}{x^2-1} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{2-x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{x^2-2}{x^3-6x+1} \cdot dx</math> | ||
| + | #<math>\int \cfrac{7x}{x^2+3} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{x \cdot ln\,x} \cdot dx</math> | ||
| + | |||
| + | |url1=https://youtu.be/duuygXo-gIs?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplos 4 | ||
| + | |duracion=7'18" | ||
| + | |sinopsis= | ||
| + | #<math>\int sen(4x+3) \cdot dx</math> | ||
| + | #<math>\int cos\left(\cfrac{2x}{5}\right) \cdot dx</math> | ||
| + | #<math>\int tan\left({x}{6}\right) \cdot dx</math> | ||
| + | #<math>\int x^2 \cdot sen(x^3) \cdot dx</math> | ||
| + | #<math>\int 3e^x \cdot tan(e^x) \cdot dx</math> | ||
| + | |url1=https://youtu.be/YDgbUTE5EYo?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplos 5 | ||
| + | |duracion=14'57" | ||
| + | |sinopsis= | ||
| + | #<math>\int \cfrac{1}{1+(3x)^2} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{1+9x^2} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{1+7x^2} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{4+x^2} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{5+x^2} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{3+2x^2} \cdot dx</math> | ||
| + | |url1=https://youtu.be/-ZdFG_DT4lM?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | }} | ||
| }} | }} | ||
| + | |||
| + | De esta manera tenemos las siguientes integrales inmediatas: | ||
| + | |||
| + | [[Imagen:int_inmediatas.png|500px|center]] | ||
| {{p}} | {{p}} | ||
| {{ejemplo2 | {{ejemplo2 | ||
| - | |titulo=Ejemplos: ''Primitivas inmediatas'' | + | |titulo=Ejercicios resueltos: ''Primitivas inmediatas'' |
| - | |enunciado=Primitivas del tipo \int [u(x)]^m \cdot u'(x) \cdot dx \quad m \ne -1<math></math> | + | |enunciado=Primitivas del tipo <math>\int [u(x)]^m \cdot u'(x) \cdot dx \quad (m \ne -1)</math> |
| - | {{Video_enlace2 | + | {{Videotutoriales|titulo=Ejercicios|enunciado= |
| - | |titulo1=1. Ejemplo | + | {{Video_enlace_fonemato |
| - | |duracion='" | + | |titulo1=Ejercicio 1 |
| + | |duracion=7'01" | ||
| |sinopsis= | |sinopsis= | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/01/in01_05a1.html | + | #<math>\int 4x^3(1+x^4)^{20} \cdot dx</math> |
| + | #<math>\int 3(3x+5)^7 \cdot dx</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=N4yIQcm-8zY&list=PLECA0C7A8B59E5534&index=5 | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_fonemato |
| - | |titulo1=2. Ejemplo | + | |titulo1=Ejercicio 2 |
| - | |duracion='" | + | |duracion=10'22" |
| + | |sinopsis=*Primitivas del tipo <math>\int x^m \cdot dx</math> <math>(m \ne 1)</math>. Ejemplos | ||
| + | *Ejercicios: | ||
| + | #<math>\int \left( x^2 +x^4+x^7+x^{19} \right) \cdot dx</math> | ||
| + | #<math>\int \left( \cfrac{1}{x^3} + \cfrac{1}{x^5} + \cfrac{1}{x^6}\right) \cdot dx</math> | ||
| + | #<math>\int \left( \sqrt{x} + \sqrt[3]{x} + \sqrt[6]{x} + \sqrt[8]{x}\right) \cdot dx</math> | ||
| + | #<math>\int \left( \cfrac{1}{\sqrt[5]{x}} + \cfrac{1}{\sqrt[7]{x}} + \cfrac{1}{\sqrt[9]{x}}\right) \cdot dx</math> | ||
| + | #<math>\int \left( 5x^4 -3x^6+9x^8 \right) \cdot dx</math> | ||
| + | #<math>\int \left( 5 -3\sqrt{x}+9\sqrt[5]{x} \right) \cdot dx</math> | ||
| + | #<math>\int \sqrt{x}(1-x) \cdot dx</math> | ||
| + | #<math>\int x(5x^2+2x) \cdot dx</math> | ||
| + | #<math>\int x^2(5x+\cfrac{7}{x^2}) \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=Q39Gp0SZEgA&list=PLECA0C7A8B59E5534&index=6 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=10'12" | ||
| + | |sinopsis=*Primitivas del tipo <math>\int x^m \cdot dx</math> <math>(m \ne 1)</math> en las que hay que aplicar el binomio de Newton. | ||
| + | *Ejercicios: | ||
| + | #<math>\int \left( 1+\sqrt{x} \right)^2 \cdot dx</math> | ||
| + | #<math>\int \left( 3x^2-x \right)^2 \cdot dx</math> | ||
| + | #<math>\int \left( 2+ \sqrt[3]{x} \right)^3 \cdot dx</math> | ||
| + | #<math>\int \left( 2- \sqrt[3]{x} \right)^3 \cdot dx</math> | ||
| + | #<math>\int \left( 2+\sqrt{x} \right)^4 \cdot dx</math> | ||
| + | |||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-integral/01-calculo-de-primitivas-2/050103-cinco-ejercicios-con-la-formula-del-binomio-de-newton-2 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=6'27" | ||
| |sinopsis= | |sinopsis= | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/01/in01_05a2.html | + | #<math>\int e^x(1+e^x)^3 \cdot dx</math> |
| + | #<math>\int 6x^5(1+x^6)^{10} \cdot dx</math> | ||
| + | #<math>\int (1+3x^2)(x+x^3)^{13} \cdot dx</math> | ||
| + | #<math>\int 3\sqrt{1+3x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{5}{\sqrt{1+5x}} \cdot dx</math> | ||
| + | #<math>\int (1+sen \, x)^6 \cdot cos \, x \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=XB-d0p0db14&index=8&list=PLECA0C7A8B59E5534 | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_fonemato |
| - | |titulo1=3. Ejemplo | + | |titulo1=Ejercicio 5 |
| - | |duracion='" | + | |duracion=13'31" |
| |sinopsis= | |sinopsis= | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/01/in01_05a3.html | + | #<math>\int x(7+x^2)^5 \cdot dx</math> |
| + | #<math>\int e^{3x}(2+e^{3x})^4 \cdot dx</math> | ||
| + | #<math>\int x^2\sqrt{1+x^3} \cdot dx</math> | ||
| + | #<math>\int x^2\sqrt{1+x^4} \cdot dx</math> | ||
| + | #<math>\int \cfrac{x^2}{\sqrt{1-x^3}} \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=sXRYwteboXE&list=PLECA0C7A8B59E5534&index=9 | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_fonemato |
| - | |titulo1=4. Ejemplo | + | |titulo1=Ejercicio 6 |
| - | |duracion='" | + | |duracion=6'31" |
| |sinopsis= | |sinopsis= | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/01/in01_05a4.html | + | #<math>\int \cfrac{1}{x\sqrt[4]{1-ln \, x}} \cdot dx</math> |
| + | #<math>\int \cfrac{sen \, 3x}{\sqrt[5]{1-cos \, 3x}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{x}(1+ln \, x)^3 \cdot dx</math> | ||
| + | #<math>\int \cfrac{7}{\sqrt[3]{1+7x}} \cdot dx</math> | ||
| + | #<math>\int 2\sqrt[3]{1+2x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{sen \, x}{1-cos \, x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{cos \, x}{\sqrt[3]{1+sen \, x}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{x\sqrt[4]{1+ln \, x}} \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=I_7AHvOYw6E&list=PLECA0C7A8B59E5534&index=11 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=10'59" | ||
| + | |sinopsis= | ||
| + | #<math>\int 4^x \sqrt{1+4^x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{\sqrt{1+tg \, 2x}}{cos^2 \, 2x} \cdot dx</math> | ||
| + | #<math>\int \sqrt{1+sen \, 4x} \cdot (cos \, 4x) \cdot dx</math> | ||
| + | #<math>\int \cfrac{\sqrt[4]{1+cotg \, 3x}}{sen^2 \, 3x} \cdot dx</math> | ||
| + | #Determine la función "f" tal que: f(0)=0, f'(0)=5, f''(0)=1 y f'''(x)=x+1 | ||
| + | #Determine la primitiva de <math>f(x)=sen \, x \cdot cos \,x </math> que pasa por el origen. | ||
| + | |||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-integral/01-calculo-de-primitivas-2/050107-seis-ejercicios-2 | ||
| + | }} | ||
| }} | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{ejemplo2 | ||
| + | |titulo=Ejercicios resueltos: ''Primitivas inmediatas'' | ||
| + | |enunciado=Primitivas del tipo <math>\int \cfrac{u'(x)}{u(x)} \cdot dx</math> | ||
| + | {{Videotutoriales|titulo=Ejercicios|enunciado= | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=8'16" | ||
| + | |sinopsis= | ||
| + | #<math>\int \cfrac{3x^2}{5+x^3} \cdot dx</math> | ||
| + | #<math>\int \cfrac{e^x}{7+e^x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{1-2x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{x+a} \cdot dx</math> | ||
| + | #<math>\int \left( \cfrac{2}{x+3} + \cfrac{5}{x-7} \right) \cdot dx</math> | ||
| + | #<math>\int \cfrac{4x^3-5x^2+8}{x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{ax+b} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{1+x^2} \cdot dx</math> | ||
| + | #<math>\int tg \, 5x \cdot dx</math> | ||
| + | #<math>\int cotg \, 4x \cdot dx</math> | ||
| + | |||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-integral/01-calculo-de-primitivas-2/050201-diez-ejercicios-2 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=4'26" | ||
| + | |sinopsis= | ||
| + | #<math>\int \cfrac{3}{(5+tg \,3x)\cdot cos^2 \,3x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{cos \, 3x}{1-sen \, 3x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{sen \, 7x}{1+cos \, 7x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{x ln \, x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{e^{6x}}{1-e^{6x}} \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=NlccyO0ZeuM&list=PLECA0C7A8B59E5534&index=13 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=2'36" | ||
| + | |sinopsis= | ||
| + | #<math>\int \cfrac{1}{\sqrt{x} \cdot (1+\sqrt{x})} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{\sqrt[3]{x} \cdot (1+\sqrt[3]{x^2})} \cdot dx</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=Rpv48O6LvWY&list=PLECA0C7A8B59E5534&index=14 | ||
| + | }} | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{ejemplo2 | ||
| + | |titulo=Ejercicios resueltos: ''Primitivas inmediatas'' | ||
| + | |enunciado=Primitivas del tipo <math>\int u'(x)^\cdot a^{u(x)} \cdot dx \quad a>0</math> | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=10'25" | ||
| + | |sinopsis= | ||
| + | #<math>\int 5x^4 \cdot 7^{x^5} \cdot dx</math> | ||
| + | #<math>\int 4x^3 e^{x^4} \cdot dx</math> | ||
| + | #<math>\int e^{sen \, x} \cdot cos \, x \cdot dx</math> | ||
| + | #<math>\int e^{kx} \cdot dx</math> | ||
| + | #<math>\int e^{5x} \cdot dx</math> | ||
| + | #<math>\int e^{2x} \cdot dx</math> | ||
| + | #<math>\int e^{\frac{x}{6}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{3^{arctg \, x}}{1+x^2} \cdot dx</math> | ||
| + | #<math>\int \cfrac{5^{arcsen \, x}}{\sqrt{1-x^2}} \cdot dx</math> | ||
| + | #<math>\int x \cdot e^{x^2} \cdot dx</math> | ||
| + | #<math>\int \cfrac{5^{\sqrt{x}}}{\sqrt{x}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{x \cdot 3^{\sqrt{1-x^2}}}{\sqrt{1-x^2}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{x \cdot 5^{arcsen \, x^2}}{\sqrt{1-x^4}} \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=cXr-eCstlug&list=PLECA0C7A8B59E5534&index=15 | ||
| + | }} | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{ejemplo2 | {{ejemplo2 | ||
| |titulo=Ejemplos: ''Primitivas inmediatas'' | |titulo=Ejemplos: ''Primitivas inmediatas'' | ||
| - | |enunciado=Primitivas del tipo \int \cfrac{u'(x)}{u(x) \cdot dx<math></math> | + | |enunciado=Primitivas del tipo <math>\int u'(x) \cdot sen \, u(x) \cdot dx \quad a>0</math> |
| - | {{Video_enlace2 | + | {{Video_enlace_fonemato |
| - | |titulo1=1. Ejemplo | + | |titulo1=Ejercicio 1 |
| - | |duracion='" | + | |duracion=6'33" |
| |sinopsis= | |sinopsis= | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/01/in01_05b1.html | + | #<math>\int \cfrac{sen \, (ln \, x)}{x} \cdot dx</math> |
| + | #<math>\int \cfrac{x \cdot sen \, \sqrt{1+x^2}}{\sqrt{1+x^2}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{3 \cdot sen \, (tg \, 3x)}{cos^2 \, 3x} \cdot dx</math> | ||
| + | #<math>\int x^2 \cdot sen \, x^3 \cdot dx</math> | ||
| + | #<math>\int (cos \, x)\cdot sen \, (sen \, x) \cdot dx</math> | ||
| + | #<math>\int \cfrac{sen \, \sqrt{x}}{\sqrt{x}} \cdot dx</math> | ||
| + | #<math>\int e^{2x} \cdot sen \, e^{2x} \cdot dx</math> | ||
| + | #<math>\int sen \, kx \cdot dx</math> | ||
| + | #<math>\int sen \, 2x \cdot dx</math> | ||
| + | #<math>\int sen \, 5x \cdot dx</math> | ||
| + | #<math>\int sen \, \cfrac{x}{7} \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=xfdmR1WK2aw&list=PLECA0C7A8B59E5534&index=16 | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | }} |
| - | |titulo1=2. Ejemplo | + | {{p}} |
| - | |duracion='" | + | {{ejemplo2 |
| + | |titulo=Ejercicios resueltos: ''Primitivas inmediatas'' | ||
| + | |enunciado=Primitivas del tipo <math>\int u'(x) \cdot cos \, u(x) \cdot dx \quad a>0</math> | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=7'28" | ||
| + | |sinopsis= | ||
| + | #<math>\int 3x^2 \cdot cos \, x^3 \cdot dx</math> | ||
| + | #<math>\int \cfrac{3x^2 \cdot cos \, \sqrt{1+x^3}}{2 \, \sqrt{1+x^3}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{5 \, cos \, (tg \, 5x)}{cos^2 \, 5x} \cdot dx</math> | ||
| + | #<math>\int x^3 \cdot cos \, x^4 \cdot dx</math> | ||
| + | #<math>\int e^{3x} \cdot cos \, e^{3x} \cdot dx</math> | ||
| + | #<math>\int (cos \, x)\cdot cos \, (sen \, x) \cdot dx</math> | ||
| + | #<math>\int \cfrac{cos \, (ln \, x^5)}{x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{cos \, \sqrt{x}}{\sqrt{x}} \cdot dx</math> | ||
| + | #<math>\int cos \, kx \cdot dx</math> | ||
| + | #<math>\int cos \, 2x \cdot dx</math> | ||
| + | #<math>\int cos \, 5x \cdot dx</math> | ||
| + | #<math>\int cos \, \cfrac{x}{7} \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=ofuhd4q8lTE&list=PLECA0C7A8B59E5534&index=17 | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{ejemplo2 | ||
| + | |titulo=Ejercicios resueltos: ''Primitivas inmediatas'' | ||
| + | |enunciado=Primitivas del tipo <math>\int \cfrac{u'(x)}{cos^2 \, u(x)} \cdot dx</math> | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=6'39" | ||
| + | |sinopsis= | ||
| + | #<math>\int \cfrac{3x^2}{cos^2 \, x^3} \cdot dx</math> | ||
| + | #<math>\int \cfrac{3x^2}{2 \, \sqrt{1+x^3} \cdot cos^2 \, \sqrt{1+x^3}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{2 \, \sqrt{x} \cdot cos^2 \, \sqrt{x}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{x^3}{cos^2 \, x^4} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{x \cdot cos^2 \, (ln \, x^7)} \cdot dx</math> | ||
| + | #<math>\int \cfrac{5^x}{cos^2 \, 5^x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{sen \, x}{cos^2 \, (cos \, x)} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{\sqrt{1-x} \cdot cos^2 \, \sqrt{1-x}} \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=15AOaW50xDI&index=19&list=PLECA0C7A8B59E5534 | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{ejemplo2 | ||
| + | |titulo=Ejercicios resueltos: ''Primitivas inmediatas'' | ||
| + | |enunciado=Primitivas del tipo <math>\int \cfrac{u'(x)}{sen^2 \, u(x)} \cdot dx</math> | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=5'24" | ||
| + | |sinopsis= | ||
| + | #<math>\int \cfrac{1}{2 \, \sqrt{x} \cdot sen^2 \, \sqrt{x}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{x^4}{sen^2 \, x^5} \cdot dx</math> | ||
| + | #<math>\int \cfrac{3^x}{sen^2 \, 3^x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{sen \, x}{sen^2 \, (cos \, x)} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{x \cdot sen^2 \, (ln \, x^3)} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{\sqrt{1+x} \cdot sen^2 \, \sqrt{1+x}} \cdot dx</math> | ||
| + | |url1=https://www.youtube.com/watch?v=05mXNQAehUI&index=20&list=PLECA0C7A8B59E5534 | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{ejemplo2 | ||
| + | |titulo=Ejercicios resueltos: ''Primitivas inmediatas'' | ||
| + | |enunciado=Primitivas del tipo <math>\int \cfrac{u'(x)}{a^2+[u(x)]^2} \cdot dx</math> | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=12'49" | ||
| + | |sinopsis= | ||
| + | #<math>\int \cfrac{4x^3}{9+x^8} \cdot dx</math> | ||
| + | #<math>\int \cfrac{3e^{3x}}{25+e^{6x}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{x^2}{21+x^6} \cdot dx</math> | ||
| + | #<math>\int \cfrac{cos \, 7x}{5+sen^2 \, 7x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{2 \, sen \, x \cdot cos \, x}{9+sen^4 \, x} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{\sqrt{x} \cdot (5+x)} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{9+5x^2} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{5+2x+x^2} \cdot dx</math> | ||
| + | #<math>\int \cfrac{4x^{\frac{1}{3}}}{3(13 + x^{\frac{8}{3}})} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{x \cdot (17+(ln \, x)^2)} \cdot dx</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=S-jHBiuP3HU&index=21&list=PLECA0C7A8B59E5534 | ||
| + | }} | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | {{ejemplo2 | ||
| + | |titulo=Ejercicios resueltos: ''Primitivas inmediatas'' | ||
| + | |enunciado=Primitivas del tipo <math>\int \cfrac{u'(x)}{\sqrt{a^2-[u(x)]^2}} \cdot dx</math> | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=10'49" | ||
| |sinopsis= | |sinopsis= | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/01/in01_05b2.html | + | #<math>\int \cfrac{4x^3}{\sqrt{9-x^8}} \cdot dx</math> |
| + | #<math>\int \cfrac{x^2}{\sqrt{21-x^6}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{3e^{3x}}{\sqrt{25-e^{6x}}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{cos \, 7x}{\sqrt{5-sen^2 \, 7x}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{\sqrt{x} \cdot \sqrt{5-x}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{2 \, sen \, x \cdot cos \, x}{\sqrt{9-sen^4 \, x}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{4x^{\frac{1}{3}}}{3 \sqrt{15 - x^{\frac{8}{3}}})} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{\sqrt{3+2x-x^2}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{x \cdot \sqrt{17-(ln \, x)^2}} \cdot dx</math> | ||
| + | #<math>\int \cfrac{1}{\sqrt{9-5x^2}} \cdot dx</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=I5qHYmugB2E&index=22&list=PLECA0C7A8B59E5534 | ||
| }} | }} | ||
| }} | }} | ||
| + | |||
| + | |||
| + | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Integrales inmediatas básicas
Empezaremos viendo aquellas funciones cuyas primitivas son las funciones elementales. Basta con recordar las reglas de derivación que vimos en un tema anterior y que puedes ver en el siguiente enlace: Ver reglas de derivación.
Reglas básicas de integración:
- Integral de un número.
- Integral de una potencia.
Reglas básicas de integración:
- Integral de una potencia (ampliación).
- Integral del logaritmo neperiano.
Reglas básicas de integración:
- Integral de funciones exponenciales.
Reglas básicas de integración:
- Integral de funciones trigonométricas.
Reglas básicas de integración:
- Integral de funciones trigonométricas (ampliación).
Integrales inmediatas
En este apartado estudiaremos las integrales de funciones cuyas primitivas son funciones compuestas. Más concretamente:
Proposición
Demostración:
Es inmediato si a partir de la derivada de la función compuesta
Integrales inmediatas.
Integrales inmediatas (continuación).
Integrales inmediatas (continuación).
Integrales inmediatas
De esta manera tenemos las siguientes integrales inmediatas:
Ejercicios resueltos: Primitivas inmediatas
Primitivas del tipo ![\int [u(x)]^m \cdot u'(x) \cdot dx \quad (m \ne -1)](/wikipedia/images/math/d/0/b/d0b6088fa26b6d625de05c0a40b70602.png)
- Primitivas del tipo
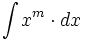
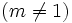 . Ejemplos
. Ejemplos
- Ejercicios:
- Primitivas del tipo
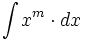
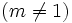 en las que hay que aplicar el binomio de Newton.
en las que hay que aplicar el binomio de Newton.
- Ejercicios:
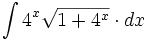
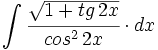
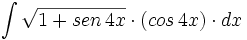
![\int \cfrac{\sqrt[4]{1+cotg \, 3x}}{sen^2 \, 3x} \cdot dx](/wikipedia/images/math/8/f/2/8f234b8b662cc63a891d726b7da2ec0c.png)
- Determine la función "f" tal que: f(0)=0, f'(0)=5, f(0)=1 y f'(x)=x+1
- Determine la primitiva de
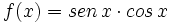 que pasa por el origen.
que pasa por el origen.
Ejercicios resueltos: Primitivas inmediatas
Primitivas del tipo 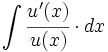
![\int g'[f(x)] \cdot f'(x) \, dx = g[f(x)] + k](/wikipedia/images/math/4/a/c/4ac140003f37d4a5b81c5a8a97b2711a.png)
![(g[f(x)])'= g[f(x)] \cdot f'(x)](/wikipedia/images/math/b/4/a/b4ae8c3c9234d3b604838ba41fb43497.png)
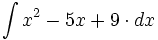
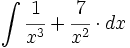
![\int \sqrt[4]{x} \cdot dx](/wikipedia/images/math/b/7/3/b73dc75d6fbb51951f525349789d3264.png)
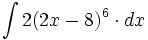
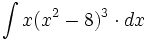
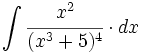
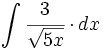
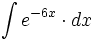
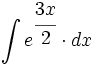
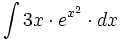
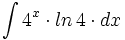
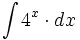
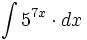
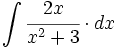
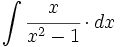
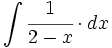
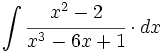
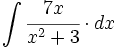
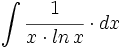
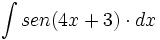
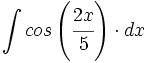
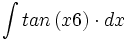
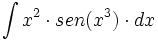
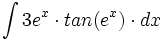
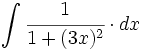
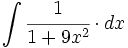
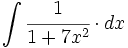
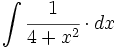
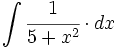
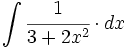

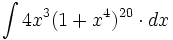
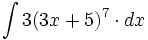
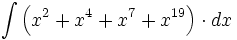
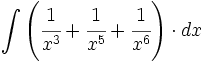
![\int \left( \sqrt{x} + \sqrt[3]{x} + \sqrt[6]{x} + \sqrt[8]{x}\right) \cdot dx](/wikipedia/images/math/a/d/7/ad7b72d3dc41c911a4cf21a1642eeead.png)
![\int \left( \cfrac{1}{\sqrt[5]{x}} + \cfrac{1}{\sqrt[7]{x}} + \cfrac{1}{\sqrt[9]{x}}\right) \cdot dx](/wikipedia/images/math/6/4/7/6472b81d1d67dc15b37e43230a2dd291.png)
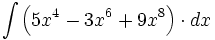
![\int \left( 5 -3\sqrt{x}+9\sqrt[5]{x} \right) \cdot dx](/wikipedia/images/math/8/a/9/8a9fe9ee2f33c419cf96dc0ee568039f.png)
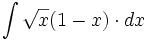
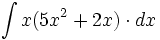
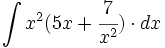
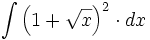
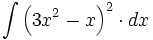
![\int \left( 2+ \sqrt[3]{x} \right)^3 \cdot dx](/wikipedia/images/math/4/1/4/414d418a1a496473d75f833b5d26fc12.png)
![\int \left( 2- \sqrt[3]{x} \right)^3 \cdot dx](/wikipedia/images/math/a/4/4/a4489d3417128570c75d0ec26f905bf9.png)
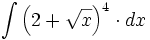
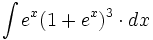
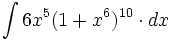
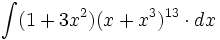
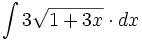
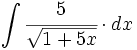
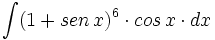
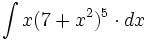
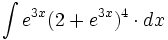
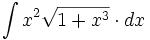
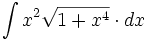
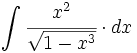
![\int \cfrac{1}{x\sqrt[4]{1-ln \, x}} \cdot dx](/wikipedia/images/math/c/f/c/cfc07daf2baefd842e5848f0f7e03f42.png)
![\int \cfrac{sen \, 3x}{\sqrt[5]{1-cos \, 3x}} \cdot dx](/wikipedia/images/math/f/e/d/fedd75fa6e1b4fc832a1b3244d31d706.png)
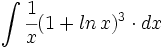
![\int \cfrac{7}{\sqrt[3]{1+7x}} \cdot dx](/wikipedia/images/math/3/e/c/3ec4553d16d4a020caac805f5621e032.png)
![\int 2\sqrt[3]{1+2x} \cdot dx](/wikipedia/images/math/9/1/9/919dbc3b549d0ed508a6e32d4f1eb63f.png)
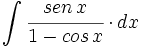
![\int \cfrac{cos \, x}{\sqrt[3]{1+sen \, x}} \cdot dx](/wikipedia/images/math/7/1/d/71d9e7ee213b836b85f2bed8530bad51.png)
![\int \cfrac{1}{x\sqrt[4]{1+ln \, x}} \cdot dx](/wikipedia/images/math/3/6/e/36e712c3e51f2f00db9567790cce7502.png)
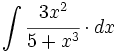
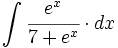
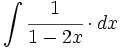
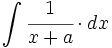
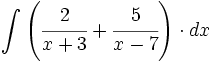
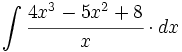
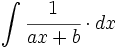
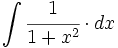
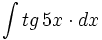
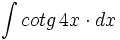
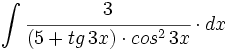
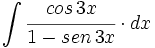
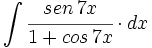
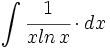
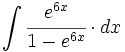
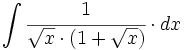
![\int \cfrac{1}{\sqrt[3]{x} \cdot (1+\sqrt[3]{x^2})} \cdot dx](/wikipedia/images/math/e/0/0/e00ec3c06bca7273fafc77dfb13d2365.png)
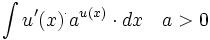
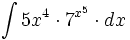
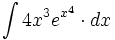
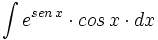
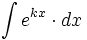
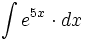
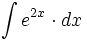
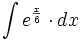
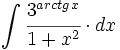
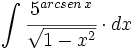
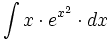
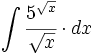
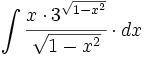
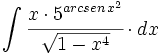
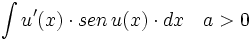
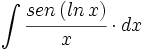
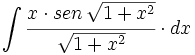
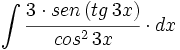
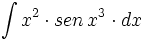
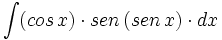
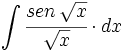
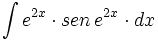
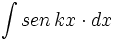
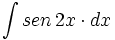
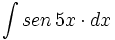
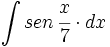
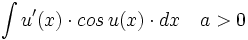
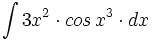
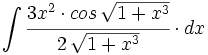
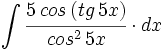
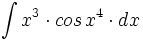
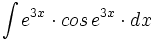
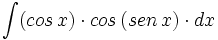
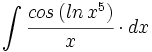
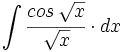
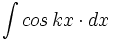
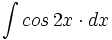
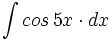
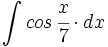
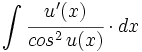
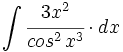
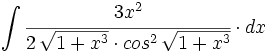
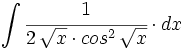
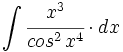
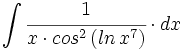
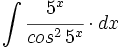
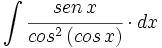
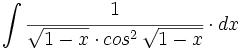
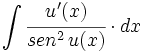
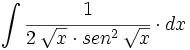

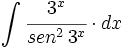
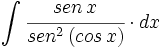
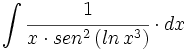
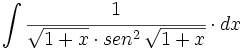
![\int \cfrac{u'(x)}{a^2+[u(x)]^2} \cdot dx](/wikipedia/images/math/1/2/1/1216aad7e7c8189456878755ca0c846c.png)
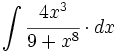
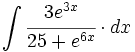
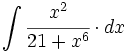
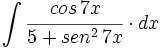
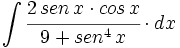
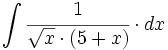
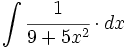
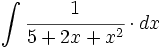
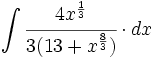
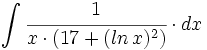
![\int \cfrac{u'(x)}{\sqrt{a^2-[u(x)]^2}} \cdot dx](/wikipedia/images/math/7/0/e/70e26d7ca7ea8762b35e39fea301f6a4.png)