Integral definida (2ºBach)
De Wikipedia
| Revisión de 11:07 27 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Introducción) |
||
| Línea 1: | Línea 1: | ||
| + | ==Introducción== | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Qué es integrar | ||
| + | |duracion=12'38" | ||
| + | |url1=https://youtu.be/0Pyjd_s2Q-4?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | |sinopsis=Qué es integrar. Una aproximación al concepto de integración. | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Qué significa integrar | ||
| + | |duracion=10'05" | ||
| + | |sinopsis= | ||
| + | Para que todo sea fácil cuando hablemos de integrales, es imprescindible que entendamos el significado del verbo integrar en el lenguaje coloquial. | ||
| + | Piensa en lo que sucede cuando la nave de los malos se desintegra al recibir el impacto del rayo láser de los buenos. Pues integrar es lo contrario que desintegrar; es sinónimo de sumar, adicionar, reunir, agregar... | ||
| + | Para las Matemáticas la idea es la misma... pero nosotros vamos a integrar (sumar, adicionar...) áreas de rectángulos. | ||
| + | ¿Por qué nos da la manía de integrar (sumar, adicionar...) áreas de rectángulos? En este video te lo contamos. | ||
| + | |url1=https://www.youtube.com/watch?v=5K6NBbsAC_o&index=43&list=PLECA0C7A8B59E5534 | ||
| + | }} | ||
| + | |||
| + | ==Integral definida== | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Integral definida. Regla de Barrow. | ||
| + | |duracion=12'47" | ||
| + | |url1=https://youtu.be/VIIXxanNF3o?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | |sinopsis=La integral definida: Área entre una función y el eje X. Regla de Barrow. Ejemplos con Geogebra. | ||
| + | }} | ||
| + | |||
| + | |||
| + | ==Ejercicios== | ||
| {{Videotutoriales|titulo=Integrales definidas inmediatas|enunciado= | {{Videotutoriales|titulo=Integrales definidas inmediatas|enunciado= | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
Revisión actual
Introducción
Qué es integrar. Una aproximación al concepto de integración.
Para que todo sea fácil cuando hablemos de integrales, es imprescindible que entendamos el significado del verbo integrar en el lenguaje coloquial. Piensa en lo que sucede cuando la nave de los malos se desintegra al recibir el impacto del rayo láser de los buenos. Pues integrar es lo contrario que desintegrar; es sinónimo de sumar, adicionar, reunir, agregar... Para las Matemáticas la idea es la misma... pero nosotros vamos a integrar (sumar, adicionar...) áreas de rectángulos. ¿Por qué nos da la manía de integrar (sumar, adicionar...) áreas de rectángulos? En este video te lo contamos.
Integral definida
La integral definida: Área entre una función y el eje X. Regla de Barrow. Ejemplos con Geogebra.
Ejercicios
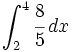
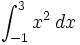
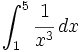
![\int_{-3}^{-1} \sqrt[3]{x^2} \, dx](/wikipedia/images/math/3/e/f/3ef78dfc1afd5490f8140c018cd83d2a.png)
![\int_{1}^{4} \sqrt[3]{27t} \, dt](/wikipedia/images/math/6/4/a/64af5171106055e85891eaee3fbc4713.png)
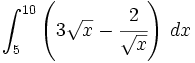
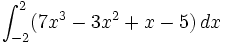
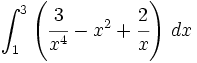
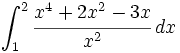
Calcula 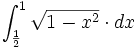 haciendo el cambio de variable
haciendo el cambio de variable 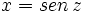 .
.
Calcula 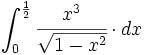 .
.
Calcula No se pudo entender (error de sintaxis): \int_{0}^{1} \cfrac{x^3+3x^2-3x}{x^2+3x+2}} \cdot dx .

