Cálculo de áreas (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:48 26 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Video_enlace_fonemato | + | ==Área entre una función y el eje X== |
| - | |titulo1=¿Qué significa integrar? | + | {{Video_enlace_pildoras |
| - | |duracion=10'05" | + | |titulo1=Área entre una función y el eje X |
| + | |duracion=12'09" | ||
| + | |url1=https://youtu.be/A4kctby_Ki4?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | |sinopsis=A la hora de calcular el área hay que tener cuidado con el "signo" de ésta. Ejemplos. | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=16'01" | ||
| + | |url1=https://youtu.be/04PhtWZwWC0?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| |sinopsis= | |sinopsis= | ||
| - | Para que todo sea fácil cuando hablemos de integrales, es imprescindible que entendamos el significado del verbo integrar en el lenguaje coloquial. | + | #Calcula el área entre la función <math>y=2x-3\;</math>, el eje X y las rectas x=-1 y x=2. |
| - | Piensa en lo que sucede cuando la nave de los malos se desintegra al recibir el impacto del rayo láser de los buenos. Pues integrar es lo contrario que desintegrar; es sinónimo de sumar, adicionar, reunir, agregar... | + | #Calcula el área entre la función <math>y=x^3-x^2-6x\;</math> y el eje X. |
| - | Para las Matemáticas la idea es la misma... pero nosotros vamos a integrar (sumar, adicionar...) áreas de rectángulos. | + | #Calcula el área entre la función <math>y=ln\,x</math>, el eje X y las rectas x=1 y x=4. |
| - | ¿Por qué nos da la manía de integrar (sumar, adicionar...) áreas de rectángulos? En este video te lo contamos. | + | }} |
| - | |url1=https://www.youtube.com/watch?v=5K6NBbsAC_o&index=43&list=PLECA0C7A8B59E5534 | + | {{Video_enlace_pildoras |
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=15'28" | ||
| + | |url1=https://youtu.be/YPrFvsSpWEk?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | |sinopsis= | ||
| + | #Calcula el área del recinto acotado limitado por la curva <math>y=\cfrac{ln\,x}{x}</math> y las rectas y=0 y x=e. | ||
| + | #Calcula el área entre la función <math>y=(6-x)e^{\frac{x-4}{3}}-1\;</math>, el eje X y las rectas x=2 y x=4. | ||
| + | #Calcula el área entre la función <math>y=2cos\,x+x-1</math>, el eje X y las rectas <math>x=\pi</math> y <math>x=2\pi</math>. | ||
| + | }} | ||
| + | ==Área entre dos funciones== | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Área entre dos funciones | ||
| + | |duracion=9'35" | ||
| + | |url1=https://youtu.be/o-2Bt8v_v4o?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | |sinopsis=Cálculo del área entre dos funciones. Ejemplo con Geogebra. | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=11'56" | ||
| + | |url1=https://youtu.be/JB3Fgto7rjQ?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | |sinopsis= | ||
| + | #Calcula el área comprendida entre las funciones <math>f(x)=x^2-3\;</math> y <math>g(x)=2x\;</math>. | ||
| + | #Calcula el área comprendida entre las funciones <math>f(x)=x^2\;</math> y <math>g(x)=x\;</math> y las rectas x=0 y x=2. | ||
| + | #Calcula el área comprendida entre las funciones <math>f(x)=x^2\;</math> y <math>g(x)=\sqrt{x}\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=20'37" | ||
| + | |url1=https://youtu.be/z0f7nYfMWmI?list=PLwCiNw1sXMSBA1KORgh0feSngW7ZUWF3b | ||
| + | |sinopsis= | ||
| + | #Calcula el área comprendida entre las funciones <math>f(x)=x^3-x+1\;</math> y la recta tangente a ella en el punto de abscisa x=1. | ||
| + | #Calcula el área comprendida entre las funciones <math>f(x)=-x^2+4x\;</math> y las rectas tangentes a ella en los puntos de corte con el eje X. | ||
| + | #Calcula el área comprendida entre las funciones <math>f(x)=x^2-2x+1\;</math>, su recta tangente en el punto (3,4) y el eje X. | ||
| + | #Calcula el área comprendida entre la curva <math>f(x)=\cfrac{1-x^2}{x^2+1}\;</math> y la recta <math>y=1-x\;</math>. | ||
| }} | }} | ||
Revisión actual
[editar]
Área entre una función y el eje X
Área entre una función y el eje X (12'09") Sinopsis:A la hora de calcular el área hay que tener cuidado con el "signo" de ésta. Ejemplos.
Ejercicio 1 (16'01") Sinopsis:- Calcula el área entre la función
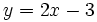, el eje X y las rectas x=-1 y x=2.
- Calcula el área entre la función
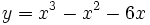y el eje X.
- Calcula el área entre la función
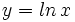, el eje X y las rectas x=1 y x=4.
Ejercicio 2 (15'28") Sinopsis:- Calcula el área del recinto acotado limitado por la curva
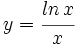y las rectas y=0 y x=e.
- Calcula el área entre la función
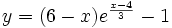, el eje X y las rectas x=2 y x=4.
- Calcula el área entre la función
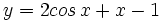, el eje X y las rectas x = π y x = 2π.
[editar]
Área entre dos funciones
Área entre dos funciones (9'35") Sinopsis:Cálculo del área entre dos funciones. Ejemplo con Geogebra.
Ejercicio 1 (11'56") Sinopsis:- Calcula el área comprendida entre las funciones
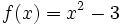y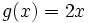 
.
- Calcula el área comprendida entre las funciones
y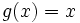 
y las rectas x=0 y x=2.
- Calcula el área comprendida entre las funciones y
.
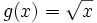Ejercicio 2 (20'37") Sinopsis:- Calcula el área comprendida entre las funciones
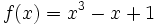y la recta tangente a ella en el punto de abscisa x=1.
- Calcula el área comprendida entre las funciones
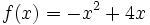y las rectas tangentes a ella en los puntos de corte con el eje X.
- Calcula el área comprendida entre las funciones
, su recta tangente en el punto (3,4) y el eje X.
- Calcula el área comprendida entre la curva
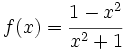y la recta 
.
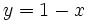