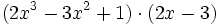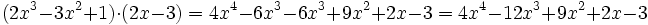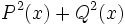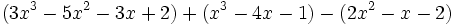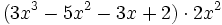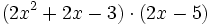Plantilla:Producto de polinomios
De Wikipedia
| Revisión de 13:15 12 ene 2018 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 54: | Línea 54: | ||
| |url1=https://www.youtube.com/watch?v=c5-VdhPQ9Xo&list=PLw7Z_p6_h3oxU1jHlHchenHoWdC0XkGCi&index=4 | |url1=https://www.youtube.com/watch?v=c5-VdhPQ9Xo&list=PLw7Z_p6_h3oxU1jHlHchenHoWdC0XkGCi&index=4 | ||
| }} | }} | ||
| - | + | {{Video_enlace_pildoras | |
| + | |titulo1=Tutorial 5 | ||
| + | |duracion=8'08" | ||
| + | |sinopsis=Producto de polinomios. | ||
| + | |url1=https://youtu.be/39JKQr3PP0o?list=PLwCiNw1sXMSDgbsuqToHr0F45-YoSUP7d | ||
| + | }} | ||
| ---- | ---- | ||
| '''Producto de binomios:''' | '''Producto de binomios:''' | ||
Revisión actual
Procedimiento
Para multiplicar dos polinomios, se multiplica cada monomio de uno de sus factores por todos y cada uno de los monomios del otro factor y, después, se suman los monomios semejantes obtenidos.
Aprende a multiplicar binomios
Aprende a multiplicar polinomios
En este tutorial se explica la multiplicación de monomios y polinomios comenzando con algunas definiciones básicas y terminando con ejemplos.
Producto de monomios y polinomios en una variable.
Cómo se multiplican polinomios.
Propiedades conmutativa y asociativa del producto de polinomios.
Elemento neutro y distributiva en el producto de polinomios.
Producto de polinomios.
Producto de binomios:
Multiplica (x − 4)(x + 7).
Multiplica (3x + 2)(5x − 7).
Halla el área de la figura dada en el video, expresándola como el producto de dos binomios y como un trinomio.
Producto de binomios por polinomios:
Multiplica 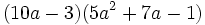 .
.
Halla el área de la figura dada en el video.
Halla el valor de "a" y "b" sabiendo que 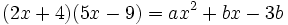 .
.
Producto de polinomios:
Multiplica:
- a)
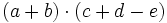
- b)
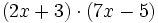
- c)
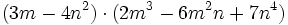
- d)
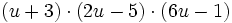
Multiplica:
- a)
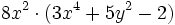
- b)
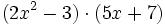
- c)
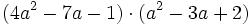
Determinar el polinomio que tiene por raíces: 2, 3 y -1, siendo la última raíz de multiplicidad 2.
Haz las siguientes multiplicaciones de polinomios:
- a)
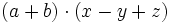
- b)
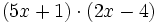
- c)
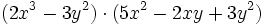
- d)
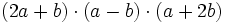
Dados los polinomios
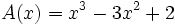 ;
; 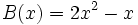 ;
; 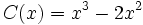
determina:
- a)
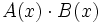
- b)
![C(x) \cdot [A(x)+ B(x)]\;](/wikipedia/images/math/e/0/8/e08fa9a42dff804cada0dd81daf805b8.png)
Multiplica los siguientes polinomios en columna e indicar el grado de los factores y del producto.
- 3a)
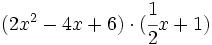
- 3b)
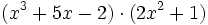
- 3c)
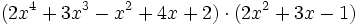
- 4a) Comprueba la propiedad conmutativa del producto de polinomios con los polinomios siguientes:
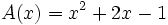 ;
; 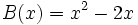
- 4b) Comprueba la propiedad asociativa del producto de polinomios con los polinomios siguientes:
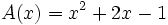 ;
; 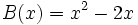 ; C(x)=x-2\;</math>
; C(x)=x-2\;</math>
- 5) Elemento neutro del producto de polinomios: Multiplica el polinomio
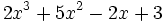 por el polinomio
por el polinomio 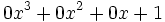 . ¿Qué polinomio obtienes?
. ¿Qué polinomio obtienes?
- 6a) Comprueba la propiedad conmutativa del producto de polinomios con los polinomios siguientes:
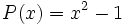 ;
; 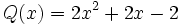
- 6b) Comprueba la propiedad asociativa del producto de polinomios con los polinomios siguientes:
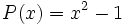 ;
; 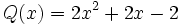 ;
; 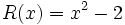
- 7a) Comprueba la propiedad distributiva del producto respecto de la suma de polinomios
![P(x) \cdot [Q(x)+R(x)]\;](/wikipedia/images/math/b/9/6/b96fc101039408c7ae1321f879455e95.png)
con los polinomios siguientes:
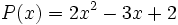 ;
; 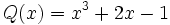 ;
; 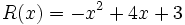
- 7b) Dados los polinomios
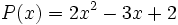 ;
; 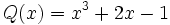
calcula
teniendo en cuenta que 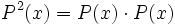 .
.
Dados los polinomios:
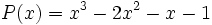 ;
; 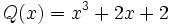 ;
;
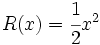 ;
; 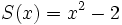
calcula:
- 8a)
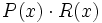
- 8b)
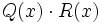
- 8c)
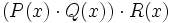
- 8d)
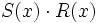
- 8e)
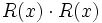
Dados los polinomios:
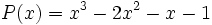 ;
; 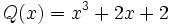 ;
;
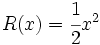 ;
; 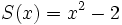
calcula:
- 8f)
![[P(x)]^2 \cdot R(x)\;](/wikipedia/images/math/2/3/e/23e83f298368c1a8c3119ea50a751be1.png)
- 8g)
![[Q(x)]^2\;](/wikipedia/images/math/f/c/0/fc0c585adb8c3eb99ba38d3006893145.png)
- 8h)
![[Q(x)]^2 \cdot S(x)\;](/wikipedia/images/math/5/d/c/5dce56fdbd0aef855ffaa69a67baf805.png)
calcula hallando previamente el grado de los factores y del producto:
- 9a)
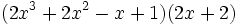
- 9b)
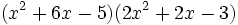
- 9c)
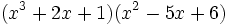
- 9d)
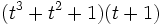
- 9e)
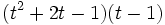
- 9f)
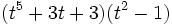
Calcula:
- 10a)
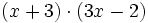
- 10b)
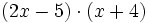
- 10c)
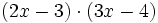
- 10d)
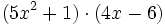
- 10e)
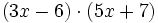
- 10f)
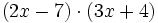
Completa:
- a) Si grado de P(x)=1 y grado de Q(x)=3, el grado de P(x)·Q(x) es ...
- b) Si grado de P(x)=2 y grado de Q(x)=4, el grado de P(x)·Q(x) es ...
- c) Si grado de P(x)=1 y grado de Q(x)=3, el grado de P(x)·Q(x) es ...
- d) Si grado de P(x)=6 y grado de Q(x)=1, el grado de P(x)·Q(x) es ...
Problemas:
Halla el volumen de un depósito cuya base tiene un área de 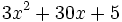 metros cuadrados y una altura de
metros cuadrados y una altura de 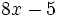 metros.
metros.
Escribe un binomio que exprese la diferencia entre el área de un rectángulo que mide "p" de largo y "2r" de ancho, y el área de un círculo cuyo diámetro mide 4r.
La parte de vidrio de una ventana tiene una proporción de 3:2 entre su largo y su ancho (la altura la podemos representar como 3x y la anchura como 2x). El marco de la ventana añade 7 cm al ancho total y 8 cm al alto total. Encuentra un polinomio, en términos de "x", que represente el área total de la ventana, incluyendo el marco.
Actividades para aprender y practicar la multiplicación de polinomios.
Multiplicación de binomios.
Multiplicación de binomios.
Multiplicación de binomios por polinomios.
Ejercicios de autoevaluación sobre producto de de polinomios.
|
Actividad: Operaciones con polinomios Haz las siguientes operaciones con polinomios:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) expand (3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2) b) expand (3x^3-5x^2-3x+2)*2x^2 c) expand (2x^2+2x-3)*(2x-5) |