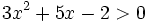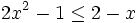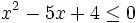Plantilla:Inecuaciones cuadráticas con una incógnita
De Wikipedia
| Revisión de 21:11 15 dic 2017 Coordinador (Discusión | contribuciones) (→Con ´dos incógnitas) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Resolución de inecuaciones cuadráticas con una incógnita) |
||
| Línea 29: | Línea 29: | ||
| |sinopsis=Inecuaciones de segundo grado con una incógnita. Ejemplos. | |sinopsis=Inecuaciones de segundo grado con una incógnita. Ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=f8tqkJfJZek&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=80 | + | |url1=http://www.youtube.com/watch?v=f8tqkJfJZek&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=80 |
| }} | }} | ||
| {{Video_enlace_matemovil | {{Video_enlace_matemovil | ||
| Línea 36: | Línea 36: | ||
| |sinopsis=Inecuaciones de segundo grado con una incógnita. Ejemplos. | |sinopsis=Inecuaciones de segundo grado con una incógnita. Ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=agrcLibSxPg&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=81 | + | |url1=http://www.youtube.com/watch?v=agrcLibSxPg&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=81 |
| }} | }} | ||
| ---- | ---- | ||
| - | Método: por intervalos (tabla de signos): | + | '''Método: por intervalos (tabla de signos):''' |
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
| Línea 58: | Línea 58: | ||
| |duracion=4'36" | |duracion=4'36" | ||
| |sinopsis=Resuelve: <math>9-x^2 > 0\;</math> | |sinopsis=Resuelve: <math>9-x^2 > 0\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=43kKD145Bno&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=1 | + | |url1=http://www.youtube.com/watch?v=43kKD145Bno&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=1 |
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| Línea 64: | Línea 64: | ||
| |duracion=5'17" | |duracion=5'17" | ||
| |sinopsis=Resuelve: <math>x^2-x \ge 20\;</math> | |sinopsis=Resuelve: <math>x^2-x \ge 20\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=rQtiGBtEhZY&index=2&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n | + | |url1=http://www.youtube.com/watch?v=rQtiGBtEhZY&index=2&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n |
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| Línea 70: | Línea 70: | ||
| |duracion=5'15" | |duracion=5'15" | ||
| |sinopsis=Resuelve: <math>5x-x^2 < 0\;</math> | |sinopsis=Resuelve: <math>5x-x^2 < 0\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=3rKS0ffwPZU&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=3 | + | |url1=http://www.youtube.com/watch?v=3rKS0ffwPZU&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=3 |
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| Línea 76: | Línea 76: | ||
| |duracion=6'26" | |duracion=6'26" | ||
| |sinopsis=Resuelve: <math>x^2-3x+6 \le 2x+2\;</math> | |sinopsis=Resuelve: <math>x^2-3x+6 \le 2x+2\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=p3Sv3Wa5qYQ&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=4 | + | |url1=http://www.youtube.com/watch?v=p3Sv3Wa5qYQ&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=4 |
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| Línea 82: | Línea 82: | ||
| |duracion=9'54" | |duracion=9'54" | ||
| |sinopsis=Resuelve: <math>6x^2-7x-3 \le 0\;</math> | |sinopsis=Resuelve: <math>6x^2-7x-3 \le 0\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=0XrkCpV6fnc&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=5 | + | |url1=http://www.youtube.com/watch?v=0XrkCpV6fnc&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=5 |
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| Línea 88: | Línea 88: | ||
| |duracion=8'31" | |duracion=8'31" | ||
| |sinopsis=Resuelve: <math>2x^2-5x-3 > 0\;</math> | |sinopsis=Resuelve: <math>2x^2-5x-3 > 0\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=sxzDHspZgzQ&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=6 | + | |url1=http://www.youtube.com/watch?v=sxzDHspZgzQ&list=PLo7_lpX1yruM63QFpb53lBOw3Rcwpzv6n&index=6 |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| Línea 95: | Línea 95: | ||
| |sinopsis=Resuelve: <math>x(x-2) \ge 3\;</math> | |sinopsis=Resuelve: <math>x(x-2) \ge 3\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=CiCp1-3n3sU | + | |url1=http://www.youtube.com/watch?v=CiCp1-3n3sU |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| Línea 102: | Línea 102: | ||
| |sinopsis=Resuelve: <math>x(3x+2) > (x+2)^2\;</math> | |sinopsis=Resuelve: <math>x(3x+2) > (x+2)^2\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=kmLnD8c-uJA | + | |url1=http://www.youtube.com/watch?v=kmLnD8c-uJA |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| Línea 109: | Línea 109: | ||
| |sinopsis=Resuelve: <math>(x-5)(x-4) \le 6\;</math> | |sinopsis=Resuelve: <math>(x-5)(x-4) \le 6\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=wzV2ZkKhB7A | + | |url1=http://www.youtube.com/watch?v=wzV2ZkKhB7A |
| + | }} | ||
| + | {{Video_enlace_miguematicas | ||
| + | |titulo1=Ejercicio 11 | ||
| + | |duracion=8'23" | ||
| + | |sinopsis=Resuelve: <math>5x(x-2) \ge 3x+6\;</math> | ||
| + | |||
| + | |url1=https://youtu.be/2JvXJC0lD-A?list=PLLfTN7MHLxConbepI-_1OEy-pjAxI8IvH | ||
| }} | }} | ||
| ---- | ---- | ||
| - | Método: analizando el signo de los factores / por intervalos: | + | '''Método: analizando el signo de los factores / por intervalos:''' |
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 118: | Línea 125: | ||
| |duracion=9'32" | |duracion=9'32" | ||
| |sinopsis=Resuelve: <math>(x+2)(x-1)>0\;</math> analizando el signo de los factores. | |sinopsis=Resuelve: <math>(x+2)(x-1)>0\;</math> analizando el signo de los factores. | ||
| - | |url1=https://www.youtube.com/watch?v=yceN3wUEoeI&index=30&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | + | |url1=http://www.youtube.com/watch?v=yceN3wUEoeI&index=30&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 124: | Línea 131: | ||
| |duracion=6'52" | |duracion=6'52" | ||
| |sinopsis=Resuelve: <math>(x+2)(x-1)>0\;</math> analizando el signo por intervalos. | |sinopsis=Resuelve: <math>(x+2)(x-1)>0\;</math> analizando el signo por intervalos. | ||
| - | |url1=https://www.youtube.com/watch?v=LL0UtfD_YYU&index=31&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | + | |url1=http://www.youtube.com/watch?v=LL0UtfD_YYU&index=31&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 130: | Línea 137: | ||
| |duracion=6'52" | |duracion=6'52" | ||
| |sinopsis=Resuelve: <math>x^2+5x+4<0\;</math> analizando el signo de los factores. | |sinopsis=Resuelve: <math>x^2+5x+4<0\;</math> analizando el signo de los factores. | ||
| - | |url1=https://www.youtube.com/watch?v=dslzOFEwNkY&index=32&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | + | |url1=http://www.youtube.com/watch?v=dslzOFEwNkY&index=32&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 136: | Línea 143: | ||
| |duracion=7'07" | |duracion=7'07" | ||
| |sinopsis=Resuelve: <math>x^2+5x+4<0\;</math> analizando el signo por intervalos. | |sinopsis=Resuelve: <math>x^2+5x+4<0\;</math> analizando el signo por intervalos. | ||
| - | |url1=https://www.youtube.com/watch?v=7pgShvH5Qfs&index=33&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | + | |url1=http://www.youtube.com/watch?v=7pgShvH5Qfs&index=33&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 142: | Línea 149: | ||
| |duracion=8'45" | |duracion=8'45" | ||
| |sinopsis=Resuelve: <math>x^2+2x \ge x+6\;</math> analizando el signo de los factores. | |sinopsis=Resuelve: <math>x^2+2x \ge x+6\;</math> analizando el signo de los factores. | ||
| - | |url1=https://www.youtube.com/watch?v=o7-1dnvhMv0&index=34&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | + | |url1=http://www.youtube.com/watch?v=o7-1dnvhMv0&index=34&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 148: | Línea 155: | ||
| |duracion=7'50" | |duracion=7'50" | ||
| |sinopsis=Resuelve: <math>x^2+2x \ge x+6\;</math> analizando el signo por intervalos. | |sinopsis=Resuelve: <math>x^2+2x \ge x+6\;</math> analizando el signo por intervalos. | ||
| - | |url1=https://www.youtube.com/watch?v=sc3zJeMtFII&index=35&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | + | |url1=http://www.youtube.com/watch?v=sc3zJeMtFII&index=35&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 154: | Línea 161: | ||
| |duracion=7'10" | |duracion=7'10" | ||
| |sinopsis=Resuelve: <math>x^2+5x-2 \le x-2\;</math> analizando el signo de los factores. | |sinopsis=Resuelve: <math>x^2+5x-2 \le x-2\;</math> analizando el signo de los factores. | ||
| - | |url1=https://www.youtube.com/watch?v=AAYOU3QIZOY&index=36&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | + | |url1=http://www.youtube.com/watch?v=AAYOU3QIZOY&index=36&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 160: | Línea 167: | ||
| |duracion=7'18" | |duracion=7'18" | ||
| |sinopsis=Resuelve: <math>x^2+5x-2 \le x-2\;</math> analizando el signo por intervalos. | |sinopsis=Resuelve: <math>x^2+5x-2 \le x-2\;</math> analizando el signo por intervalos. | ||
| - | |url1=https://www.youtube.com/watch?v=QUkdNCE5_mw&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=37 | + | |url1=http://www.youtube.com/watch?v=QUkdNCE5_mw&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=37 |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 166: | Línea 173: | ||
| |duracion=7'44" | |duracion=7'44" | ||
| |sinopsis=Resuelve: <math>x^2 < 9\;</math> analizando el signo de los factores. | |sinopsis=Resuelve: <math>x^2 < 9\;</math> analizando el signo de los factores. | ||
| - | |url1=https://www.youtube.com/watch?v=sq98v0gHvLg&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=38 | + | |url1=http://www.youtube.com/watch?v=sq98v0gHvLg&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=38 |
| }} | }} | ||
| Línea 173: | Línea 180: | ||
| |duracion=7'22" | |duracion=7'22" | ||
| |sinopsis=Resuelve: <math>x^2 < 9\;</math> analizando el signo por intervalos. | |sinopsis=Resuelve: <math>x^2 < 9\;</math> analizando el signo por intervalos. | ||
| - | |url1=https://www.youtube.com/watch?v=vCFX0G8YJuo&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=39 | + | |url1=http://www.youtube.com/watch?v=vCFX0G8YJuo&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=39 |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 179: | Línea 186: | ||
| |duracion=8'53" | |duracion=8'53" | ||
| |sinopsis=Resuelve: <math>25 \ge 4x^2\;</math> analizando el signo de los factores. | |sinopsis=Resuelve: <math>25 \ge 4x^2\;</math> analizando el signo de los factores. | ||
| - | |url1=https://www.youtube.com/watch?v=uUFsC0HOF8I&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=40 | + | |url1=http://www.youtube.com/watch?v=uUFsC0HOF8I&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=40 |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 185: | Línea 192: | ||
| |duracion=8'28" | |duracion=8'28" | ||
| |sinopsis=Resuelve: <math>25 \ge 4x^2\;</math> analizando el signo por intervalos. | |sinopsis=Resuelve: <math>25 \ge 4x^2\;</math> analizando el signo por intervalos. | ||
| - | |url1=https://www.youtube.com/watch?v=QFpdR-yDUek&index=41&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | + | |url1=http://www.youtube.com/watch?v=QFpdR-yDUek&index=41&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo |
| }} | }} | ||
| }} | }} | ||
| Línea 245: | Línea 252: | ||
| }} | }} | ||
| }} | }} | ||
| - | |||
| - | ==Sistemas de inecuaciones con una incógnita== | ||
| - | {{Sistema de inecuaciones con una incógnita}} | ||
| - | {{p}} | ||
| - | ==Inecuaciones con fracciones algebraicas con una incógnita== | ||
| - | {{Videos: Inecuaciones con fracciones algebraicas}} | ||
| - | |||
| - | ==Otras inecuaciones con una incógnita== | ||
| - | {{Inecuaciones polinómicas}} | ||
| - | {{Inecuaciones con valores absolutos}} | ||
| - | {{p}} | ||
| - | {{Video_enlace_unicoos | ||
| - | |titulo1=Inecuación con radicales | ||
| - | |duracion=8'36" | ||
| - | |sinopsis=1 ejemplo. | ||
| - | |url1=http://www.unicoos.com/video/matematicas/2-bachiller/inecuaciones-y-sistemas/inecuaciones-con-radicales/inecuacion-con-radicales | ||
| - | }} | ||
| - | {{p}} | ||
| - | ==Inecuación lineal con dos incógnitas== | ||
| - | {{Inecuación lineal con dos incógnitas}} | ||
| - | {{p}} | ||
| - | ===Resolución de una inecuación lineal con dos incógnitas=== | ||
| - | {{Resolución de una inecuación lineal con dos incógnitas}} | ||
| - | {{p}} | ||
| - | ==Sistemas de inecuaciones lineales con dos incógnitas== | ||
| - | {{Sistemas de inecuaciones lineales con dos incógnitas}} | ||
| - | {{p}} | ||
| - | ===Resolución de un sistema de inecuaciones lineales con dos incógnitas=== | ||
| - | {{Resolución de un sistema de inecuaciones lineales con dos incógnitas}} | ||
| - | {{p}} | ||
| - | ==Ejercicios== | ||
| - | ===Con una incógnita=== | ||
| - | {{Ejercicios: Inecuaciones con una incógnita}} | ||
| - | ===Con dos incógnitas=== | ||
| - | {{Ejercicios: Inecuaciones lineales con dos incógnitas}} | ||
| - | |||
| - | {{p}} | ||
Revisión actual
Una inecuación cuadrática con una incógnita es una inecuación en la que las expresiones matemáticas que intervienen en la desigualdad, son polinomios de segundo grado en una sola variable. En consecuencia, puede ponerse, mediante transformaciones, de alguna de estas formas:
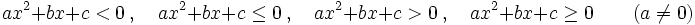
Resolución de inecuaciones cuadráticas con una incógnita
Para resolver estas inecuaciones usaremos el método gráfico. Este método requiere que el miembro de la derecha de la inecuación sea cero, lo cual siempre se puede conseguir mediante transformaciones.
Inecuaciones de segundo grado con una incógnita. Ejemplos.
Inecuaciones de segundo grado con una incógnita. Ejemplos.
Inecuaciones de segundo grado con una incógnita. Ejemplos.
Método: por intervalos (tabla de signos):
Resuelve:
- a)
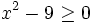
- b)
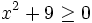
- c)
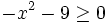
- d)
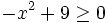
Resuelve: 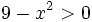
Resuelve: 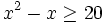
Resuelve: 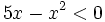
Resuelve: 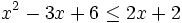
Resuelve: 
Resuelve: 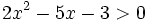
Resuelve: 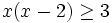
Resuelve: 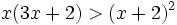
Resuelve: 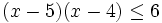
Resuelve: 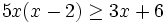
Método: analizando el signo de los factores / por intervalos:
Resuelve: 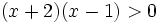 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 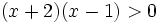 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 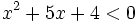 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 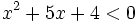 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 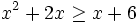 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 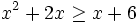 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 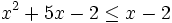 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 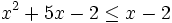 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 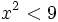 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 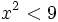 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 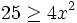 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 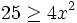 analizando el signo por intervalos.
analizando el signo por intervalos.
En la escena vamos a resolver la siguiente inecuación:
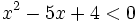
Representamos la parábola 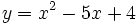 y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa).
y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa).
En realidad basta hallar los puntos de corte con el eje X y determinar la dirección de las ramas a partir del signo del coeficiente de 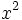 .
.
En este caso, los puntos de corte son 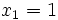 y
y 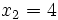 , soluciones de la ecuación de segundo grado
, soluciones de la ecuación de segundo grado
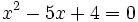
y las ramas va hacia arriba porque el coeficiente de 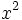 es positivo. Por tanto, las soluciones de la inecuación es:
es positivo. Por tanto, las soluciones de la inecuación es: 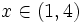 .
.
Puedes cambiar los valores A, B y C para resolver gráficamente otras inecuaciones de segundo grado.
Autoevaluación sobre inecuaciones cuadráticas.