Plantilla:Relacion de divisibilidad
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:43 25 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Dos números ''a'' y ''b'' están emparentados por la '''relación de divisibilidad''' cuando la división a:b es exacta. | + | Dos números enteros {{sube|porcentaje=10%|contenido=<math>a\;</math>}} y {{sube|porcentaje=20%|contenido=<math>b\;</math> (<math>a \ge b\;</math>)}} , están emparentados por la '''relación de divisibilidad''' cuando la división {{sube|porcentaje=20%|contenido=<math>a:b\;</math>}} es exacta. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos:|contenido= | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| - | *Un listón de 60 cm se puede partir, exactamente, en trozos de 15 cm, porque la división 60:15 es exacta (cociente=4; resto=0). Por tanto, 60 y 15 están emparentados por la relación de divisibilidad. | + | *Un listón de 60 cm se puede partir, exactamente, en trozos de 15 cm, porque la división 60:15 es exacta (cociente=4; resto=0). Por tanto, 60 y 15 '''están emparentados''' por la relación de divisibilidad. |
| - | *Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 no están emparentados por la relación de divisibilidad. | + | *Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 '''no están emparentados''' por la relación de divisibilidad. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI_enlace | + | {{Actividades|titulo=Relación de divisibilidad|enunciado= |
| - | |titulo1=Exposición: ''Relación de divisibilidad'' | + | {{AI_anaya |
| + | |titulo1=Actividad 1 | ||
| + | |descripcion=Actividad de introducción a la relación de divisibilidad. | ||
| + | |url1=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/03/01.htm | ||
| + | }} | ||
| + | {{AI_anaya | ||
| + | |titulo1=Actividad 2 | ||
| |descripcion= | |descripcion= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/03/01.htm | + | url=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/03/02.htm |
| width=800 | width=800 | ||
| height=650 | height=650 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/03/01.htm | + | |url1=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/03/02.htm |
| }} | }} | ||
| - | {{p}} | ||
| - | {{AI_enlace | ||
| - | |titulo1=Actividades: ''Relación de divisibilidad'' | ||
| - | |descripcion= | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/03/02.htm | ||
| - | width=800 | ||
| - | height=650 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/03/02.htm | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
Dos números enteros 
y 
(
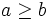) , están emparentados por la relación de divisibilidad cuando la división 
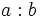es exacta.
- Un listón de 60 cm se puede partir, exactamente, en trozos de 15 cm, porque la división 60:15 es exacta (cociente=4; resto=0). Por tanto, 60 y 15 están emparentados por la relación de divisibilidad.
- Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 no están emparentados por la relación de divisibilidad.
Actividad 1 Descripción: Actividad de introducción a la relación de divisibilidad.
Actividad 2 Descripción: 
