Razones trigonométricas de un ángulo agudo (1ºBach)
De Wikipedia
| Revisión de 12:08 28 sep 2014 Coordinador (Discusión | contribuciones) (→Videotutoriales) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Razones trigonométricas de algunos ángulos importantes) |
||
| Línea 5: | Línea 5: | ||
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| + | __TOC__ | ||
| {{p}} | {{p}} | ||
| - | == Razones trigonométricas de un ángulo agudo== | + | ==Introducción== |
| - | {{Caja_Amarilla|texto=Dado un triángulo rectángulo ABC, se definen las '''razones trigonométricas''' del ángulo agudo <math> \alpha \, </math>, de la siguiente manera: | + | {{Definición de trigonometría}} |
| - | {{Tabla75|celda2= | + | |
| - | <center>[[Image:Trigono b00.png|300px]]</center> | + | |
| - | |celda1={{p}} | + | |
| - | * El '''seno''' (abreviado como ''sen'', o ''sin'' por llamarse "sinus" en latín) es la razón entre el cateto opuesto y la hipotenusa:{{p}} | + | |
| - | ::<math> sen \, \alpha= \frac{a}{c} = \frac{\overline{CB}}{\overline{AB}} </math> | + | |
| - | + | ||
| - | * El '''coseno''' (abreviado como ''cos'') es la razón entre el cateto adyacente (o contiguo) y la hipotenusa:{{p}} | + | |
| - | ::<math> cos \, \alpha= \frac{b}{c} = \frac{\overline{AC}}{\overline{AB}} </math> | + | |
| - | + | ||
| - | * La '''tangente''' (abreviado como ''tan'' o ''tg'') es la razón entre el cateto opuesto y el cateto adyacente:{{p}} | + | |
| - | ::<math> tg \, \alpha= \frac{a}{b} = \frac{\overline{CB}}{\overline{AC}} </math> | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplos|contenido= | + | ==Razones trigonométricas de un ángulo agudo== |
| - | <center><iframe> | + | {{Razones trigonométricas de un ángulo agudo}} |
| - | url=http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo1b.html | + | {{Videos y actividades: Razones trigonométricas}} |
| - | width=710 | + | {{p}} |
| - | height=250 | + | ===Razones trigonométricas inversas=== |
| - | name=myframe | + | {{Razones trigonométricas inversas}} |
| - | </iframe></center> | + | {{Videos y actividades: Razones trigonométricas inversas}} |
| - | <center>[http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo1b.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | ==Razones trigonométricas recíprocas== | + | ==Relaciones fundamentales de la trigonometría== |
| - | {{Caja_Amarilla|texto=Las '''razones trigonométricas inversas''' se definen de la siguiente manera: | + | {{Relaciones fundamentales de la trigonometría}}{{p}} |
| - | * La '''cosecante''' (abreviado como ''csc'' o ''cosec''), razón recíproca del seno:{{p}} | + | ==Razones trigonométricas de ángulos complementarios== |
| - | ::<math> cosec \, \alpha= \frac{1}{sen \, \alpha} = \frac{c}{a}</math> | + | {{Razones trigonométricas de algunos ángulos importantes}}{{p}} |
| - | + | ||
| - | * La '''secante''' (abreviado como ''sec''), razón recíproca del coseno:{{p}} | + | |
| - | ::<math> sec \, \alpha= \frac{1}{cos \, \alpha} = \frac{c}{b}</math> | + | |
| - | + | ||
| - | * La '''cotangente''' (abreviado como ''cot''), razón recíproca de la tangente:{{p}} | + | |
| - | ::<math> cot \, \alpha= \frac{1}{tg \, \alpha} = \frac{b}{a}</math> | + | |
| + | ==Ejercicios== | ||
| + | {{Videotutoriales|titulo=Razones trigonométricas|enunciado= | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=7´05" | ||
| + | |url1=https://www.youtube.com/watch?v=nu5TXKeJ5mw&list=PLHwz3md30-3mYMmrtIHx1BibUv3tim2Vi&index=5 | ||
| + | |sinopsis=Averigua los datos que te piden en la figura dada en el video. | ||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_abel |
| - | {{Video_enlace2 | + | |titulo1=Ejercicio 2 |
| - | |titulo1=Razones trigonométricas de un ángulo agudo (con brocha gorda) | + | |duracion=9´24" |
| - | |duracion=12´47" | + | |url1=https://www.youtube.com/watch?v=uuP-NFAsELs&index=6&list=PLHwz3md30-3mYMmrtIHx1BibUv3tim2Vi |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/02-razones-trigonometricas-de-un-angulo-agudo-con-brocha-gorda#.VCe_OPl_u2E | + | |sinopsis=En un triángulo rectángulo ABC, recto en C, se cumple que <math>tg\, \hat B=2 \, sec \, \hat A</math>. |
| - | |sinopsis=*Razones trigonométricas de un ángulo agudo. | + | |
| - | *Razones trigonométricas recíprocas. | + | |
| - | *Ejemplos. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=6 ejercicios (Conocida una razón trigonométrica, dibujar el ángulo) | + | |
| - | |duracion=8´19" | + | |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/0201-seis-ejercicios-conocida-una-razon-trigonometrica-dibujar-el-angulo#.VCe_kPl_u2E | + | |
| - | |sinopsis=Videotutorial | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=3 ejercicios (Hallamos razones trigonométricas con la calculadora) | + | |
| - | |duracion=9´42" | + | |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/0202-tres-ejercicios-hallamos-razones-trigonometricas-con-la-calculadora#.VCfALfl_u2E | + | |
| - | |sinopsis=Videotutorial | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=6 ejercicios (Conocida una razón trigonométrica, calcular el ángulo) | + | |
| - | |duracion=2´03" | + | |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/0203-seis-ejercicios-conocida-una-razon-trigonometrica-calcular-el-angulo#.VCfAxPl_u2E | + | |
| - | |sinopsis=Videotutorial | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Razones trigonométricas de un ángulo agudo (con pincel) | + | |
| - | |duracion=9´25" | + | |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/06-razones-trigonometricas-de-un-angulo-agudo-con-pincel#.VCfFDPl_u2E | + | |
| - | |sinopsis=*Definición razonada de las razones trigonométricas de un ángulo agudo. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{AI2|titulo=Actividad interactiva: ''Razones trigonométricas''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1:''' Practica con las razones trigonométricas y ponte a prueba con una autoevaluación | + | |
| - | |actividad={{p}} | + | |
| - | *Si pulsas el botón "EJERCICIO" cambiarán los datos del triángulo. | + | |
| - | *Si pulsas el botón "ángulo" cambiará el ángulo al que se le calculan las razones trigonométricas. | + | |
| - | *Si pulsas el botón "OTRAS RAZONES" alternararás entre las razones trigonométricas y sus recíprocas. | + | |
| - | *Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes. | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo1.html | + | |
| - | width=710 | + | |
| - | height=250 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| + | Calcula <math>E= cosec^2\,\hat A- 2\,sec\,\hat B</math>. | ||
| }} | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=5´53" | ||
| + | |url1=https://www.youtube.com/watch?v=CL7Jh7tCTkQ&index=7&list=PLHwz3md30-3mYMmrtIHx1BibUv3tim2Vi | ||
| + | |sinopsis=Averigua el valor de la expresión que te piden a partir de la figura dada en el video. | ||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_abel |
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=5´24" | ||
| + | |url1=https://www.youtube.com/watch?v=Yz46LQqonvs&index=8&list=PLHwz3md30-3mYMmrtIHx1BibUv3tim2Vi | ||
| + | |sinopsis=En un triángulo rectángulo ABC, recto en B, se cumple que <math>cotg\, \hat A=\cfrac{5}{12}</math>. | ||
| - | ==Relaciones fundamentales de la trigonometría== | + | Calcula <math>M= sen\,\hat A- sen\,\hat C</math>. |
| - | {{Teorema|titulo=Relaciones fundamentales de la trigonometría | + | |
| - | |enunciado={{p}} | + | |
| - | :'''1.''' {{Sube|porcentaje=+20%|contenido=<math>sen^2 \, \alpha + cos^2 \, \alpha = 1</math>}} | + | |
| - | {{p}} | + | |
| - | :'''2.''' <math>tg \, \alpha =\cfrac{sen \, \alpha }{cos \, \alpha}</math> | + | |
| - | :'''3.''' {{Sube|porcentaje=+20%|contenido=<math>1+tg^2 \, \alpha =\cfrac{1}{cos^2 \, \alpha}</math>}} | ||
| - | |demo= | ||
| - | '''1.''' <math>sen^2 \, \alpha + cos^2 \, \alpha = \left ( \cfrac{a}{c} \right )^2 + \left ( \cfrac{b}{c} \right )^2 =\cfrac {a^2+b^2}{c^2}= \cfrac {c^2}{c^2}=1</math> | ||
| - | |||
| - | ya que, por el [[teorema de Pitágoras]], {{Sube|porcentaje=+20%|contenido=<math>a^2+b^2=c^2\;</math>}}. | ||
| - | |||
| - | |||
| - | '''2.''' <math>\cfrac{sen \, \alpha }{cos \, \alpha}=\cfrac{a}{c}:\cfrac{b}{c}=\cfrac{a}{b}=tg \, \alpha </math> | ||
| - | |||
| - | |||
| - | '''3.''' {{Sube|porcentaje=+20%|contenido=<math>1+tg^2 \, \alpha =1+\cfrac{sen^2 \, \alpha }{cos^2 \, \alpha}=\cfrac{cos^2 \, \alpha + sen^2 \, \alpha}{cos^2 \, \alpha}=\cfrac{1}{cos^2 \, \alpha}</math>}} | ||
| - | {{p}} | ||
| - | |||
| - | donde en el último paso hemos utilizado la primera relación fundamental: {{Sube|porcentaje=+20%|contenido=<math>sen^2 \, \alpha + cos^2 \, \alpha = 1</math>}} | ||
| }} | }} | ||
| - | + | {{Video_enlace_abel | |
| - | {{Video_enlace2 | + | |titulo1=Ejercicio 5 |
| - | |titulo1=Relaciones entre las razones trigonométricas de un ángulo | + | |duracion=6´54" |
| - | |duracion=7´13" | + | |url1=https://www.youtube.com/watch?v=md5pl_6-g5M&index=9&list=PLHwz3md30-3mYMmrtIHx1BibUv3tim2Vi |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/03-relaciones-entre-las-razones-trigonometricas-de-un-angulo#.VCfBPvl_u2E | + | |sinopsis=Averigua el valor de la expresión que te piden a partir de la figura dada en el video. |
| - | |sinopsis=Videotutorial | + | |
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_abel |
| - | {{Video_enlace2 | + | |titulo1=Ejercicio 6 |
| - | |titulo1=6 ejercicios (Conocida una razón trigonométrica, hallar las otras) | + | |duracion=10´30" |
| - | |duracion=9´45" | + | |url1=https://www.youtube.com/watch?v=SIpe683DA9Y&t=183s |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/0301-seis-ejercicios-conocida-una-razon-trigonometrica-hallar-las-otras#.VCfBqfl_u2E | + | |sinopsis= |
| - | |sinopsis=Videotutorial | + | :a) Determina las 6 razones trigonométricas del mayor ángulo agudo del triángulo rectángulo ABC, recto en A, siendo b=15cm y c=8cm. |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | ===Ejercicios=== | + | |
| - | {{ejercicio | + | |
| - | |titulo=Ejercicios: ''Relaciones fundamentales de la trigonometría'' | + | |
| - | |cuerpo= | + | |
| - | + | ||
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | + | ||
| - | '''1. '''Sabiendo que {{sube|porcentaje=+15%|contenido=<math>cos \, \alpha = 0.86</math>}}, calcula <math>sen \, \alpha</math> y <math>tg \, \alpha</math>. | + | |
| - | + | ||
| - | |sol= | + | |
| - | <math>sen \, \alpha = 0.51</math> | + | |
| - | {{p}} | + | |
| - | <math>tg \, \alpha=0.59</math> | + | |
| + | :b) En un triángulo rectángulo, un cateto es el doble del otro. Calcula el coseno del mayor ángulo agudo. | ||
| }} | }} | ||
| - | {{ejercicio_cuerpo | + | {{Video_enlace_matemovil |
| - | |enunciado= | + | |titulo1=Ejercicio 7 |
| + | |duracion=22'11" | ||
| + | |sinopsis=*Razones trigonométricas directas e inversas. Propiedades. | ||
| + | *Razones trigonométricas de ángulos complementarios. | ||
| + | *Ejercicios: | ||
| + | # Calcula las 6 razones trigonométricas de <math>\alpha\;</math> sabiendo que <math>sen\,\alpha=\cfrac{3}{5}</math>. | ||
| + | # Halla el valor de <math>y\;</math> en la siguiente igualdad: <math>tg\,(2y-11) \cdot cotg\,(29-2y)=1</math> | ||
| + | ::(Pista: <math>tg\,\alpha \cdot cotg\,\alpha=1</math>) | ||
| - | '''2. '''Sabiendo que <math>tg \, \alpha= 2.83</math>, calcula <math>cos \, \alpha </math> y <math>sen \, \alpha</math> | ||
| - | |sol= | + | |url1=https://www.youtube.com/watch?v=rj0kkRM-JsM&index=11&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33 |
| - | <math>cos \, \alpha = 0.33</math> | + | |
| - | {{p}} | + | |
| - | <math>sen \, \alpha=0.93</math> | + | |
| }} | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=18'13" | ||
| + | |sinopsis=2 ejercicios en los que deberás averiguar los datos que te piden en las figuras dada en el video. | ||
| + | |url1=https://www.youtube.com/watch?v=95f_qIWR1ZU&index=12&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33 | ||
| }} | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 9 | ||
| + | |duracion=11'52" | ||
| + | |sinopsis=Halla el valor de <math>E=\cfrac{sen\,(x+y+50^\circ)}{cos\,(y-x-10^\circ)}</math> sabiendo que <math>cot\,(x+30^\circ)\cdot tg\,(y+20^\circ)=tg\,(60^\circ-x)</math>. | ||
| - | + | '''Nota:''' Recuerda que <math>tg\,45^\circ=1</math>. | |
| - | + | |url1=https://www.youtube.com/watch?v=JCN7xvZU57Q&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=13 | |
| - | ==Razones trigonométricas de algunos ángulos importantes== | + | }} |
| - | A continuación las razones trigonométricas de algunos ángulos que es conveniente recordar: | + | {{Video_enlace_matemovil |
| - | {{p}} | + | |titulo1=Ejercicio 10 |
| - | {| {{tablabonita_blanca}} | + | |duracion=12'47" |
| - | |-style="background:#e1ecf7;" align="center" | + | |sinopsis=Observa el dibujo que aparecerá en el video y asocia cada expresión del lado izquierdo con la razón trigonométrica correspondiente del lado derecho. |
| - | ! '''Radianes''' | + | |url1=https://www.youtube.com/watch?v=TTTRRz-K4zk |
| - | ! '''Grados''' | + | |
| - | ! sen | + | |
| - | ! cos | + | |
| - | ! tg | + | |
| - | ! cosec | + | |
| - | ! sec | + | |
| - | ! cot | + | |
| - | |----- | + | |
| - | | align="center" | <math> 0 \; </math> | + | |
| - | | align="center" | <math>0^o \,</math> | + | |
| - | | align="center" | <math>0 \;</math> | + | |
| - | | align="center" | <math>1 \;</math> | + | |
| - | | align="center" | <math>0 \;</math> | + | |
| - | | align="center" | <math>\not{\exists} \,\!</math> | + | |
| - | | align="center" | <math>1 \;</math> | + | |
| - | | align="center" | <math>\not{\exists} \,\!</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math> \frac{\pi}{6} </math> | + | |
| - | | align="center" | <math>30^o \,</math> | + | |
| - | | align="center" | <math>\frac{1}{2}</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{3}}{2}</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{3}}{3}</math> | + | |
| - | | align="center" | <math>2 \,</math> | + | |
| - | | align="center" | <math>\frac{2\sqrt{3}}{3}</math> | + | |
| - | | align="center" | <math>\sqrt{3}</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math> \frac{\pi}{4} </math> | + | |
| - | | align="center" | <math>45^o \,</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{2}}{2}</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{2}}{2}</math> | + | |
| - | | align="center" | <math>1 \,</math> | + | |
| - | | align="center" | <math>\sqrt{2}</math> | + | |
| - | | align="center" | <math>\sqrt{2}</math> | + | |
| - | | align="center" | <math>1 \,</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math> \frac{\pi}{3} </math> | + | |
| - | | align="center" | <math>60^o \,</math> | + | |
| - | | <math>\frac{\sqrt{3}}{2}</math> | + | |
| - | | align="center" | <math>\frac{1}{2}</math> | + | |
| - | | align="center" | <math>\sqrt{3}</math> | + | |
| - | | align="center" | <math>\frac{2\sqrt{3}}{3}</math> | + | |
| - | | align="center" | <math>2 \,</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{3}}{3}</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math> \frac{\pi}{2}</math> | + | |
| - | | align="center" | <math>90^o \,</math> | + | |
| - | | align="center" | <math>1 \;</math> | + | |
| - | | align="center" | <math>0 \;</math> | + | |
| - | | align="center" | <math>\not{\exists} \,\!</math> | + | |
| - | | align="center" | <math>1 \,</math> | + | |
| - | | align="center" | <math>\not{\exists} \,\!</math> | + | |
| - | | align="center" | <math>0 \,</math> | + | |
| - | |} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Razones trigonométricas de ángulos complementarios | + | |
| - | |duracion=4´54" | + | |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/04-razones-trigonometricas-de-angulos-complementarios#.VCfDrPl_u2E | + | |
| - | |sinopsis=Videotutorial | + | |
| }} | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace2 | ||
| - | |titulo1=Razones trigonométricas de los ángulos más famosos (0º, 30º, 45º, 60º, 90º) | ||
| - | |duracion=6´59" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/05-razones-trigonometricas-de-los-angulos-mas-famosos#.VCfETfl_u2E | ||
| - | |sinopsis=Videotutorial | ||
| }} | }} | ||
| - | {{p}} | ||
| - | |||
| - | ==Calculadora== | ||
| - | ===Funciones trigonométricas (directas)=== | ||
| - | {{Casio FX-100MS Trigonométricas}} | ||
| - | ===Funciones trigonométricas (inversas)=== | ||
| - | {{Casio FX-100MS Trigonométricas arco}} | ||
| - | |||
| - | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Introducción
La trigonometría es una rama de la matemática que estudia las relaciones entre los lados y los ángulos de un triángulo. Su significado etimológico es la medición de los triángulos, ya que deriva de los términos griegos trigōnos 'triángulo' y metron 'medida'.
- Qué es a la trigonometría.
- Triángulos: nomenclatura, propiedades y clasificación.
Razones trigonométricas de un ángulo agudo
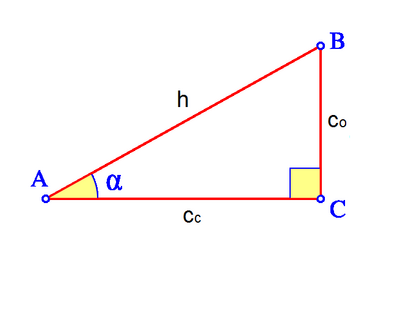
Dado un triángulo rectángulo ABC, se definen las razones trigonométricas del ángulo agudo  , de la siguiente manera:
, de la siguiente manera:
|
Razones trigonométricas de un ángulo agudo. Ejemplos.
Tutorial en el que se explica y trabaja los conceptos más básicos de la trigonometría plana, resolviendo ejercicios sencillos en los que se aplican dichas definiciones.
- 00:00 a 13:05: Conceptos y definiciones básicas. Razones trigonométricas.
- 13:05 a 17:13: Propiedades básicas trigonométricas.
- 17:13 a 25:25: Ejercicios básicos (seno, coseno, tangente).
- 25:25 a 29:05: Ejercicios básicos (arcoseno, arcocoseno, arcotangente).
- 29:05 a 37:54: Problemas de Trigonometría.
Razones trigonométricas en un triángulo rectángulo. Ejemplo.
Las definiciones de las razones trigonométricas solo dependen de valor del ángulo y no del tamaño del triángulo.
Razones trigonométricas de un ángulo agudo.
Razones trigonométricas en un triángulo rectángulo. Ejemplo.
Más ejemplos de razones trigonométricas en un triángulo rectángulo.
En esta escena podrás ver como se calculan las razones trigonométricas de un ángulo agudo.
Aprende a ubicar la hipotenusa, el cateto opuesto y el cateto adyacente de un triángulo rectángulo.
Aprende a calcular las razones trigonométricas en triángulos rectángulos.
Razones trigonométricas en triángulos rectángulos.
Razones trigonométricas inversas
Las razones trigonométricas inversas se definen de la siguiente manera:
- La cosecante (abreviado como csc o cosec), razón inversa del seno:
|
|
- La secante (abreviado como sec), razón inversa del coseno:
|
|
- La cotangente (abreviado como cot), razón inversa de la tangente:
|
|
Razones trigonométricas inversas (en el video las llama recíprocas) en un triángulo rectángulo. Ejemplo.
Las razones trigonométricas "con brocha gorda":
- Razones trigonométricas de un ángulo agudo.
- Razones trigonométricas inversas.
- Ejemplos.
Las razones trigonométricas "con pincel":
- Definición razonada de las razones trigonométricas de un ángulo agudo.
Calcula las razones trigonométricas del ángulo de la figura que te dan en el video.
Calcula las razones trigonométricas del ángulo de la figura que te dan en el video.
Calcula las razones trigonométricas del ángulo A, sabiendo que a=12, b=5 y c=13.
Calcula las restantes razones trigonométricas del ángulo 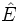 , sabiendo que
, sabiendo que 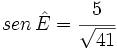 , que
, que 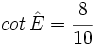 , que el lado opuesto a
, que el lado opuesto a 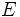 mide 5 y la hipotenusa es
mide 5 y la hipotenusa es 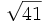 .
.
Razones trigonométricas inversas en triángulos rectángulos.
Aviso: En el video las llama recíprocas en lugar de inversas.
Razones trigonométricas directas e inversas en triángulos rectángulos:
- Si pulsas el botón "EJERCICIO" cambiarán los datos del triángulo.
- Si pulsas el botón "ángulo" cambiará el ángulo al que se le calculan las razones trigonométricas.
- Si pulsas el botón "OTRAS RAZONES" alternararás entre las razones trigonométricas y sus recíprocas.
- Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes.
Razones trigonométricas inversas en triángulos rectángulos.
Aviso: En la actividad las llama recíprocas en lugar de inversas.
Relaciones fundamentales de la trigonometría
Relaciones fundamentales de la trigonometría
1. 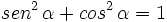 (Identidad pitagórica)
(Identidad pitagórica)
2. 
3. 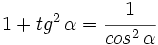
Demostración de las relaciones fundamentales de la trigonometría.
Demostración de la identidad pitagórica.
Dada una de las razones trigonométricas de un ángulo, determinar las cinco restantes, haciendo uso de las relaciones fundamentales de la trigonometría.
- a)
 ; b)
; b) 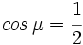 ; c)
; c) 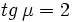
- d)
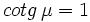 ; e)
; e) 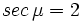 ; f)
; f) 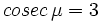
Simplifica: 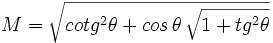
Comprueba las siguientes identidades trigonométricas:
a) 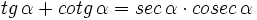
b) 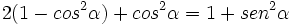
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Identidades trigonométricas. Ejercicios.
Identidades trigonométricas. Ejercicios.
Identidades trigonométricas. Ejercicios.
Ejercicio resuelto: Razones trigonométricas de un ángulo agudo
Sea
 un ángulo agudo.
un ángulo agudo.
- Sabiendo que
 , calcular
, calcular 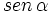 y
y 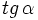 .
.
- Sabiendo que
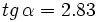 , calcular
, calcular 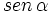 y
y 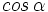 .
.
Hay que usar las relaciones fundamentales de la trigonometría para despejar la razón trigonométrica desconocida:
1. 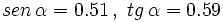
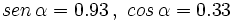
Razones trigonométricas de ángulos complementarios
Razones trigonométricas de ángulos complementarios Sea Se cumple que: Relación entre el coseno, el seno y la tangente de ángulos complementarios. Relación entre el coseno y el seno de ángulos complementarios. Razones trigonométricas de ángulos complementarios:
Halla El rio Nilo se ha desbordado y ha inundado sus alrededores, a excepción de la punta de la pirámide de Guiza. Se ha enviado una expedición para averiguar la altura que alcanzó el agua. Los exploradores midieron el borde inclinado de la pirámide que quedó fuera del agua resultando ser de 72 m. Ellos saben además que la longitud total del borde es de 180 m y que la altura de la pirámide es de 139 m. ¿Cuál es la altura del agua sobre el nivel del suelo, redondeada a dos decimales? Razones trigonométricas de ángulos complementarios. |
Ejercicios
Averigua los datos que te piden en la figura dada en el video.
En un triángulo rectángulo ABC, recto en C, se cumple que 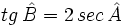 .
.
Calcula 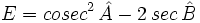 .
.
Averigua el valor de la expresión que te piden a partir de la figura dada en el video.
En un triángulo rectángulo ABC, recto en B, se cumple que 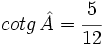 .
.
Calcula 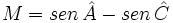 .
.
Averigua el valor de la expresión que te piden a partir de la figura dada en el video.
- a) Determina las 6 razones trigonométricas del mayor ángulo agudo del triángulo rectángulo ABC, recto en A, siendo b=15cm y c=8cm.
- b) En un triángulo rectángulo, un cateto es el doble del otro. Calcula el coseno del mayor ángulo agudo.
- Razones trigonométricas directas e inversas. Propiedades.
- Razones trigonométricas de ángulos complementarios.
- Ejercicios:
- Calcula las 6 razones trigonométricas de
 sabiendo que
sabiendo que 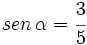 .
.
- Halla el valor de
 en la siguiente igualdad:
en la siguiente igualdad: 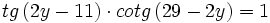
- (Pista:
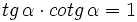 )
)
- (Pista:
2 ejercicios en los que deberás averiguar los datos que te piden en las figuras dada en el video.
Halla el valor de 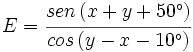 sabiendo que
sabiendo que 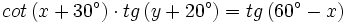 .
.
Nota: Recuerda que 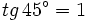 .
.
Observa el dibujo que aparecerá en el video y asocia cada expresión del lado izquierdo con la razón trigonométrica correspondiente del lado derecho.
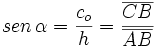

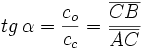
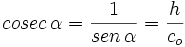
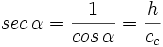
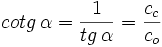


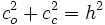
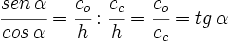
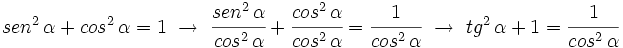
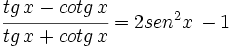
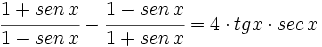
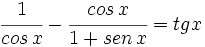
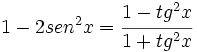
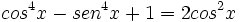
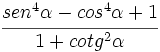
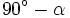 su complementario.
su complementario.
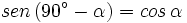
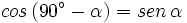
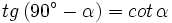
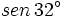 sabiendo que
sabiendo que 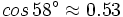 .
.