Razones trigonométricas de ángulos cualesquiera (1ºBach)
De Wikipedia
| Revisión de 19:02 15 sep 2016 Coordinador (Discusión | contribuciones) (→Circunferencia goniométrica) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Relaciones fundamentales de la trigonometría (ángulos de cualquier cuadrante)) |
||
| Línea 5: | Línea 5: | ||
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| + | __TOC__ | ||
| {{p}} | {{p}} | ||
| (Pág. 107) | (Pág. 107) | ||
| + | ==Angulos orientados== | ||
| + | {{Angulos orientados}} | ||
| + | {{p}} | ||
| ==Circunferencia goniométrica== | ==Circunferencia goniométrica== | ||
| - | Vamos a establecer un sistema de referencia para el estudio de los ángulos de cualquier cuadrante. | + | {{Circunferencia goniométrica}} |
| - | + | ||
| - | {{Caja_Amarilla|texto=Consideremos una circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con su centro en el origen de coordenadas '''O'''. Sobre ella situaremos nuestro triángulo rectángulo '''ABC''', haciendo coincidir su vértice '''A''' con '''O''', el cateto contiguo al ángulo <math>\alpha \;</math> lo situaremos en el eje X positivo y la hipotenusa coincidiendo con el radio, tal y como se muestra en la figura. A esta circunferencia la llamaremos '''circunferencia goniométrica'''. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Tabla50|celda2={{p}}<center>[[Imagen:goniometrica.png|330px]]</center> | + | ==Razones trigonométricas de un ángulo de cualquier cuadrante== |
| - | |celda1= | + | {{Razones trigonométricas de un ángulo cualquiera}} |
| - | Teniendo en cuenta que {{sube|porcentaje=+15%|contenido=<math> \overline{AB} = \overline{OE}= radio = 1 </math>}}, las razones trigonométricas del águlo <math>\alpha \;</math> se expresan de la siguiente manera: | + | |
| - | <br> | + | |
| - | + | ||
| - | *<math> sen \, \alpha = \cfrac{\overline{CB}}{\overline{AB}}=\overline{CB}</math> | + | |
| - | + | ||
| - | *<math> cos \, \alpha = \cfrac{\overline{OC}}{\overline{AB}}=\overline{OC}</math> | + | |
| - | + | ||
| - | *<math> tg \, \alpha = \cfrac{\overline{DE}}{\overline{OE}}=\overline{DE}</math> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Video_enlace | ||
| - | |titulo1=El círculo goniométrico | ||
| - | |duracion=9´14 | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/06-angulos-orientados/04-el-circulo-goniometrico#.VChMthZ8HA8 | ||
| - | |sinopsis=Videotutorial. | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | ==Razones trigonométricas de un ángulo cualquiera== | ||
| - | Obsérvese como las coordenadas del punto '''B''', del apartado anterior, son <math>(cos \, \alpha , sen \, \alpha )</math>. Así podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante: | ||
| - | |||
| - | {{Caja_Amarilla|texto= | ||
| - | *Dado un ángulo <math>\alpha \,</math>, se define el '''coseno''' y el '''seno''' de dicho ángulo, como las coordenadas del punto de corte, B, del segundo lado del ángulo con la circunferencia goniométrica: | ||
| - | |||
| - | <center><math>B=(cos \, \alpha , sen \, \alpha )</math></center> | ||
| - | |||
| - | *Definiremos la '''tangente''' del ángulo, como: | ||
| - | |||
| - | <center><math> tg \, \alpha = \cfrac{sen(\alpha)}{cos(\alpha)}</math>{{b4}},{{b4}}<math>\alpha \ne 90^\circ \, , 180^\circ</math></center> | ||
| - | }} | ||
| - | {{p}} | ||
| - | ===Signo de las razones trigonométricas=== | ||
| - | {{Caja_Amarilla|texto=Los ejes cartesianos dividen a la circunferencia goniométrica en cuatro regiones denominadas '''cuadrantes''': | ||
| - | |||
| - | *Un ángulo <math>\alpha\;</math>, pertenece al '''primer cuadrante''' si <math>0^\circ< \alpha <90^\circ</math> | ||
| - | |||
| - | *Un ángulo <math>\alpha\;</math>, pertenece al '''segundo cuadrante''' si <math>90^\circ< \alpha <180^\circ</math> | ||
| - | |||
| - | *Un ángulo <math>\alpha\;</math>, pertenece al '''tercer cuadrante''' si <math>180^\circ< \alpha <270^\circ</math> | ||
| - | |||
| - | *Un ángulo <math>\alpha\;</math>, pertenece al '''cuarto cuadrante''' si <math>270^\circ< \alpha <360^\circ</math> | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | Según en qué cuadrante estemos, el segmento OC que determina al coseno, puede estar situado a la derecha o a la izquierda del origen '''O'''. Así, asignaremos signo positivo al coseno si está a la derecha de '''O''' y negativo si está a la izquierda. | ||
| - | |||
| - | Analogamente, el segmento CB que determina al seno, puede estar situado por encima o por debajo del eje X . Asignaremos signo positivo al seno si está por encima y negativo si está por debajo. | ||
| - | |||
| - | Los siguientes gráficos muestran los distintos casos según en qué cuadrante se encuentre el ángulo: | ||
| - | |||
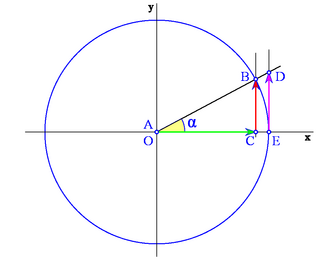
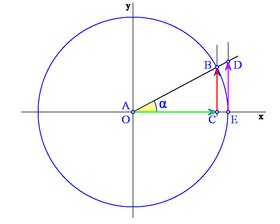
| - | {{Tabla50|celda1=<center>'''Cuadrante I <br>( seno + / cos + )''' <br> [[Imagen:goniometrica.png|280px]]</center>|celda2=<center>'''Cuadrante II <br>( seno + / cos - )''' <br> [[Imagen:goniometrica2.png|280px]]</center>}} | ||
| - | |||
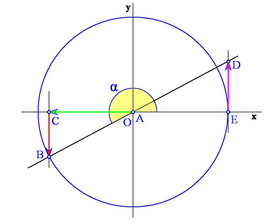
| - | {{Tabla50|celda1=<center>'''Cuadrante III <br>( seno - / cos - )''' <br> [[Imagen:goniometrica3.png|280px]]</center>|celda2=<center>'''Cuadrante IV <br>( seno - / cos + )''' <br> [[Imagen:goniometrica4.png|280px]]</center>}} | ||
| - | {{p}} | ||
| - | {{Video_enlace | ||
| - | |titulo1=Razones trigonométricas de ángulos orientados | ||
| - | |duracion=11´ | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/06-angulos-orientados/03-razones-trigonometricas-de-angulos-orientados#.VChNihZ8HA8 | ||
| - | |sinopsis=Si el lado origen de un ángulo orientado es el semieje OX, del cuadrante en que está el lado extremo se dice "cuadrante del ángulo". | ||
| - | En este video definimos las razones trigonométricas de un ángulo orientado, y para ello empleamos las coordenadas de un punto cualquiera (a;b) del lado extremo. | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace | ||
| - | |titulo1= 3 ejercicios | ||
| - | |duracion=5´53" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/06-angulos-orientados/0301-tres-ejercicios-3#.VChN-BZ8HA8 | ||
| - | |sinopsis=3 ejercicios sobre razones trigonométricas de ángulos orientados. | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace | ||
| - | |titulo1= Determinación del ángulo conocida una de sus razones trigonométricas | ||
| - | |duracion=7´38" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/06-angulos-orientados/05-determinacion-del-angulo-conocida-una-de-sus-razones-trigonometricas#.VChRtfl_vwo | ||
| - | |sinopsis=Si -1 < a < 1, en el primer giro hay dos ángulos cuyo seno es "a". | ||
| - | Si -1 < b < 1, en el primer giro hay dos ángulos cuyo coseno es "b". | ||
| - | Si "c" es un número real, en el primer giro hay dos ángulos cuyo tangente es "c". | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace | ||
| - | |titulo1= 2 ejercicios | ||
| - | |duracion=5´48" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/06-angulos-orientados/0501-dos-ejercicios#.VChRxvl_vwo | ||
| - | |sinopsis=En este vídeo empleamos la calculadora científica para determinar los dos ángulos del primer giro cuyo seno es 0.3 y los dos ángulos del primer giro cuyo seno es -0.4. | ||
| - | |||
| - | }} | ||
| - | |||
| ==Relaciones fundamentales de la trigonometría (ángulos de cualquier cuadrante)== | ==Relaciones fundamentales de la trigonometría (ángulos de cualquier cuadrante)== | ||
| - | Las [[Razones trigonométricas de un ángulo agudo (1ºBach)#Relaciones fundamentales de la trigonometría|relaciones fundamentales de la trigonometría]], ya estudiadas anteriormente, siguen siendo válidas con las definiciones dadas para ángulos de cualquier cuadrante. | + | {{Relaciones fundamentales de la trigonometría (ángulos de cualquier cuadrante)}} |
| {{p}} | {{p}} | ||
| + | ==Razones trigonométricas de 0º, 30º, 45º, 60º y 90º== | ||
| + | {{Razones trigonométricas de 0º, 30º, 45º, 60º y 90º}} | ||
| - | {{AI_enlace|titulo1=Relaciones fundamentales de la trigonometría | + | ==Razones trigonométricas de un ángulo cualquiera sin usar el círculo unidad== |
| - | |descripcion=Practica con las relaciones fundamentales de la trigonometría y ponte a prueba con una autoevaluación. En estas actividades tendrás que tener en cuenta en qué cuadrante está el ángulo para determinar el signo de la razón trigonométrica. | + | {{Razones trigonométricas de un ángulo cualquiera sin usar el círculo unidad}} |
| - | + | ||
| - | *Si pulsas el botón "EJERCICIO" cambiarán los datos del problema. | + | |
| - | *Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes. | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo6.html | + | |
| - | width=710 | + | |
| - | height=370 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | |url1=http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo6.html | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{wolfram desplegable|titulo=Razones trigonométricas de ángulos cualesquiera|contenido= | + | |
| - | {{wolfram | + | |
| - | |titulo=Actividad: ''Razones trigonométricas de ángulos cualesquiera'' | + | |
| - | |cuerpo= | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | + | ||
| - | :a) Resuelve: <math>sen\, x=0.5, \quad x \in II</math> (2º cuadrante) | + | |
| - | + | ||
| - | :b) Calcula: {{sube|porcentaje=20%|contenido=<math>cos\, 210^\circ\,</math>}} | + | |
| - | + | ||
| - | :c) Sabiendo que <math>tg \,(x) = 2, \quad x \in III</math> (3º cuadrante), halla <math>sin(x)\,</math>. | + | |
| - | + | ||
| - | {{p}} | + | |
| - | |sol= | + | |
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | + | |
| - | + | ||
| - | :a) {{consulta|texto=sin(xº)=0.5, 90<x<180}} | + | |
| - | :b) {{consulta|texto=cos(210º)}} | + | |
| - | :c) {{consulta|texto=sin(arctan(2)+180º)}} | + | |
| - | + | ||
| - | {{widget generico}} | + | |
| - | }} | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
| Línea 152: | Línea 30: | ||
| |titulo=Ejercicios propuestos: ''Razones trigonométricas de ángulos cualesquiera'' | |titulo=Ejercicios propuestos: ''Razones trigonométricas de ángulos cualesquiera'' | ||
| |cuerpo= | |cuerpo= | ||
| - | {{b4}}(Pág. 107) | + | (Pág. 107) |
| - | + | ||
| - | {{b4}}[[Imagen:red_star.png|12px]] 1,2,3 | + | |
| - | {{b4}}[[Imagen:yellow_star.png|12px]] 4 | + | [[Imagen:red_star.png|12px]] 1, 2, 3, 4 |
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
(Pág. 107)
Angulos orientados
Un ángulo orientado es aquel que, en un sistema de coordenadas cartesianas, está generado por el giro de una semirecta que parte del semieje positivo de las X. (Fig. 1)
Los ejes cartesianos dividen al plano en cuatro regiones denominadas cuadrantes:
|
Un ángulo se dice "orientado" si uno de sus lados se bautiza "lado origen" y el otro lado se bautiza "lado extremo". Si para hacer coincidir el lado origen con el lado extremo se gira alrededor del vértice en sentido contrario a las agujas del reloj, el ángulo se dice "positivo" o "levógiro", diciéndose "negativo" o "dextrógiro" si se gira en el sentido a las agujas del reloj.
Circunferencia goniométrica
Llamaremos circunferencia goniométrica a la circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con centro en el origen de coordenadas, O.
Definición y propiedades de la circunferencia goniométrica o circunferencia trigonométrica.
Sobre la circunferencia goniométrica situaremos nuestro ángulo orientado,  . Este genera un triángulo rectángulo ABC, tal y como se muestra en la Fig. 2. En él, el vértice A coincide con el origen O, el cateto OC, contiguo al ángulo . Este genera un triángulo rectángulo ABC, tal y como se muestra en la Fig. 2. En él, el vértice A coincide con el origen O, el cateto OC, contiguo al ángulo  , se situa en el eje X positivo, y la hipotenusa AB coincide con el radio. , se situa en el eje X positivo, y la hipotenusa AB coincide con el radio.
Teniendo en cuenta que |
Empleando un circulo de radio unidad pueden "visualizarse" las razones trigonométricas de un ángulo orientado.
Definición y propiedades de la circunferencia goniométrica o circunferencia trigonométrica.
Dibuja un ángulo  en los siguientes casos:
en los siguientes casos:
- 1)
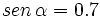 2)
2) 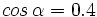 3)
3) 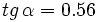
- 4)
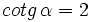 5)
5) 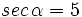 3)
3) 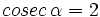
Razones trigonométricas de un ángulo de cualquier cuadrante
Obsérvese como, en el apartado anterior, las coordenadas del punto B son 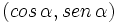 . Así podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:
. Así podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:
- Dado un ángulo
 , se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte, B, del lado terminal del ángulo con la circunferencia goniométrica:
, se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte, B, del lado terminal del ángulo con la circunferencia goniométrica:
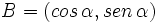
- Definiremos la tangente del ángulo, como:
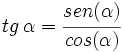 ,
, 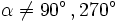
- Definición de circunferencia goniométrica o círculo unitario.
- Definición del seno, coseno y tangente de un ángulo a partir de la circunferencia goniométrica.
Asocia las expresiones equivalentes que aparecen en el video.
En esta escena podrás ver como se representan las razones trigonométricas de un ángulo de cualquier cuadrante.
Autoevaluación sobre trigonometría en el círculo unitario.
Signo de las razones trigonométricas
El signo de una razón trigonométrica viene determinado por el cuadrante en el que se encuentre el ángulo.
Signo de las razones trigonométricas
- Seno: El seno de un ángulo es positivo si el ángulo está en el primer o segundo cuadrante, y es negativo si está en el tercer o cuarto cuadrante.
- Coseno: El coseno de un ángulo es positivo si el ángulo está en el primer o cuarto cuadrante, y es negativo si está en el segundo o tercer cuadrante.
- Seno: Según el cuadrante en el que esté el ángulo, el segmento CB que determina al seno, puede estar situado por encima o por debajo del eje X . Así el signo del seno será positivo si está por encima (primer y segundo cuadrante) y negativo si está por debajo (tercer y cuarto cuadrante).
- Coseno: Según en qué cuadrante esté el ángulo, el segmento OC que determina al coseno, puede estar situado a la derecha o a la izquierda del origen O. Así, el signo del coseno será positivo si está a la derecha de O (primer y cuarto cuadrante) y negativo si está a la izquierda (segundo y tercer cuadrante).
El signo de las demás razones trigonométricas se deduce fácilmente a partir de los signos del seno y del coseno:
- El signo de la tangente queda determinado a partir del signo del seno y del coseno mediante la regla de los signos.
- El signo de las razones trigonométricas inversas (cosecante, secante y cotangente) son los mismos que los de sus respectivas razones directas (seno, coseno y tangente).
En esta escena podrás ver los valores y el signo de las 6 razones trigonométricas de un ángulo de cualquier cuadrante.
Los siguientes gráficos muestran los distintos casos según en qué cuadrante se encuentre el ángulo:
- La circunferencia goniométrica.
- Definición de las razones trigonométricas usando la circunferencia goniométrica o círculo unidad.
- Signo de las razones trigonométricas según el cuadrante con una interesante regla mnemotécnica.
- Ejemplos.
- Construcción gráfica de las razones trigonométricas usando el círculo trigonométrico.
Interpretación geométrica del seno usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica del coseno usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica de la tangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica de la cosecante usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica de la secante usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica de la cotangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
- Sabiendo que
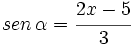 , halla el intervalo de definición de la variable
, halla el intervalo de definición de la variable  .
.
- Halla el valor de la expresión
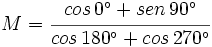 .
.
- Indica si es verdadero o falso:
- a)
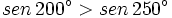
- b)
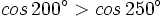
- c)
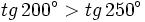
- a)
- Halla el área de las figuras sombreadas (ver video).
- Ejercicios propuestos.
Relaciones fundamentales de la trigonometría (ángulos de cualquier cuadrante)
Las relaciones fundamentales de la trigonometría, ya estudiadas anteriormente, siguen siendo válidas con las definiciones dadas para ángulos de cualquier cuadrante. Puedes verlo en el siguiente video:
Demostración de las relaciones fundamentales de la trigonometría utilizando la circunferencia goniométrica.
Demostración de las relaciones fundamentales de la trigonometría.
Si 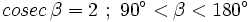 , calcula las razones trigonométricas de
, calcula las razones trigonométricas de 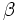
Si 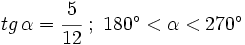 , calcula las razones trigonométricas de
, calcula las razones trigonométricas de 
Si  , calcula las razones trigonométricas de
, calcula las razones trigonométricas de 
Si 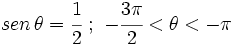 , calcula
, calcula 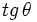 .
.
Identidad pitagórica.
Aplica el teorema fundamental para encontrar las razones trigonométricas de un ángulo de cualquier cuadrante.
|
Actividad: Razones trigonométricas de ángulos cualesquiera a) Resuelve: b) Calcula: c) Sabiendo que Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) sin(xº)=0.5, 90<x<180 b) cos(210º) c) sin(arctan(2)+180º) |
Razones trigonométricas de 0º, 30º, 45º, 60º y 90º
A continuación las razones trigonométricas de algunos ángulos que es conveniente recordar dado que vienen expresadas mediante valores exactos.
| Grados | sen | cos | tg | cosec | sec | cot |
|---|---|---|---|---|---|---|
| 
| 
| 
| 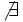
| 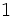
| 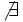
|
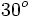
| 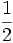
| 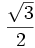
| 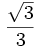
| 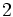
| 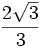
| 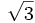
|
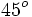
| 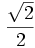
| 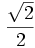
| 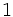
| 
| 
| 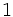
|
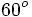
| 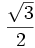
| 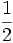
| 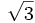
| 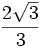
| 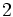
| 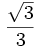
|
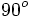
| 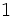
| 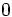
| 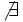
| 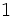
| 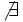
| 
|
Razones trigonométricas de 30º, 45º y 60º
Razones trigonométricas de 0º, 30º, 45º, 60º y 90º
Razones trigonométricas de 0º, 30º, 45º, 60º y 90º:
- Apoyándonos en un triángulo equilátero de lado unidad, en este vídeo determinamos las razones trigonométricas de los ángulos de 30º y 60º.
- También determinamos las razones trigonométricas del ángulo de 45º; para ello nos servimos de un triángulo rectángulo de catetos unitarios.
- Las razones trigonométricas en cuestión deben memorizarse.
Nota: Las razones de 0º y 90º se justificarán más adelante.
Una regla mnemotécnica para obtener las razones trigonométricas de 0º, 30º, 45º, 60º y 90º.
Nota: Las razones de 0º y 90º se justificarán más adelante.
Practica con las razones trigonométricas de 30º, 45º y 60º.
En esta escena de Geogebra podrás ver como se calculan las razones trigonométricas de 30º, 45º y 60º con valores exactos.
Razones trigonométricas de un ángulo cualquiera sin usar el círculo unidad
También se pueden definir las razones trigonométricas de un ángulo de cualquier cuadrante sin hacer uso del círculo unidad. Puedes verlo en los siguientes videos:
Si el lado origen de un ángulo orientado es el semieje OX, del cuadrante en que está el lado extremo se dice "cuadrante del ángulo". En este video definimos las razones trigonométricas de un ángulo orientado, y para ello empleamos las coordenadas de un punto cualquiera (a;b) del lado extremo.
Ángulos en posición normal. Ejercicios.
3 ejercicios.
3 ejercicios.
Ángulos en posición normal. Ejercicios.
Ángulos en posición normal. Ejercicios.
Ejercicios propuestos
|
Ejercicios propuestos: Razones trigonométricas de ángulos cualesquiera |
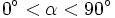
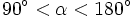
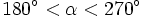
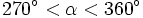

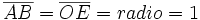
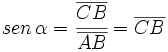
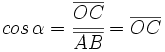
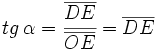


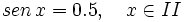 (2º cuadrante)
(2º cuadrante)
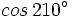
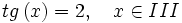 (3º cuadrante), halla
(3º cuadrante), halla 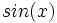 .
.

