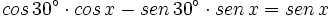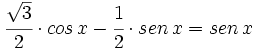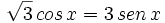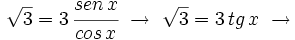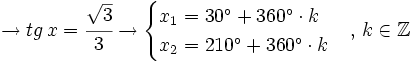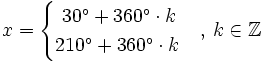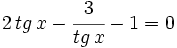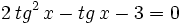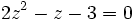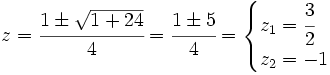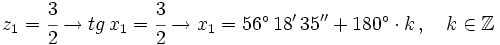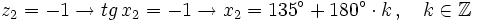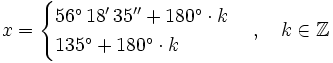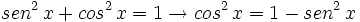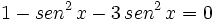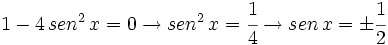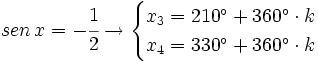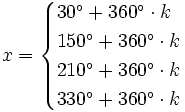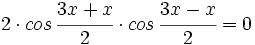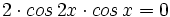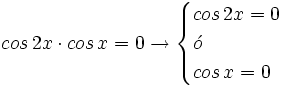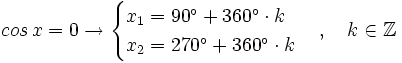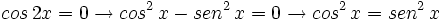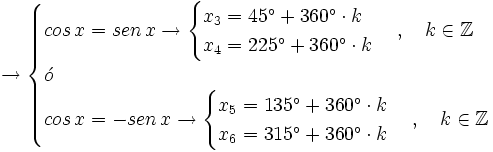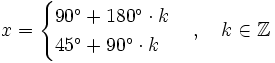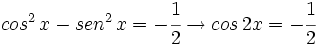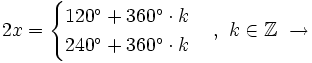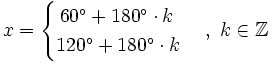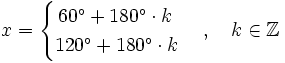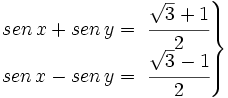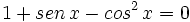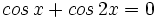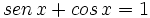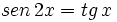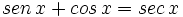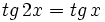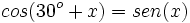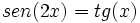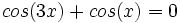Ecuaciones trigonométricas (1ºBach)
De Wikipedia
| Revisión de 11:46 30 sep 2016 Coordinador (Discusión | contribuciones) (→Ecuaciones trigonométricas) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ecuaciones trigonométricas) |
||
| Línea 18: | Línea 18: | ||
| |titulo=Ejemplos: ''Ecuaciones trigonométricas'' | |titulo=Ejemplos: ''Ecuaciones trigonométricas'' | ||
| |enunciado= | |enunciado= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado={{p}} | ||
| + | '''1. '''Resuelve: <math>cos \, (30^\circ + x)= sen \, x</math> | ||
| + | |sol= | ||
| + | '''Solución:''' | ||
| + | {{p}} | ||
| + | Desarrollamos el coseno de una suma en el primer miembro: | ||
| + | {{p}} | ||
| + | :<math>cos \, 30^\circ \cdot cos \, x - sen \, 30^\circ \cdot sen \, x = sen \, x</math> | ||
| + | {{p}} | ||
| + | :<math> \cfrac{\sqrt{3}}{2} \cdot cos \, x - \cfrac{1}{2} \cdot sen \, x = sen \, x </math> | ||
| + | {{p}} | ||
| + | :<math> \sqrt{3} \, cos \, x = 3 \, sen \, x</math> | ||
| + | {{p}} | ||
| + | Dividimos ambos miembros por <math>cos \, x</math>. (Observa que <math>cos \, x=0</math> si <math>x=90^\circ</math> ó <math>x=270^\circ</math>, valores que no cumplen la ecuación de partida. Por tanto no estaríamos dividiendo por cero y no perderíamos ninguna solución) | ||
| + | {{p}} | ||
| + | :<math>\sqrt{3} = 3 \, \cfrac{sen \, x}{cos \, x} \ \rightarrow \ \sqrt{3} = 3 \, tg \, x \ \rightarrow </math> | ||
| + | {{p}} | ||
| + | :<math>\rightarrow tg \, x = \cfrac{\sqrt{3}}{3} \rightarrow | ||
| + | \begin{cases} | ||
| + | x_1= 30^\circ + 360^\circ \cdot k | ||
| + | \\ | ||
| + | x_2=210^\circ + 360^\circ \cdot k | ||
| + | \end{cases} , \, k \in \mathbb{Z}</math> | ||
| + | '''Soluciones:''' | ||
| + | |||
| + | :<math>x= | ||
| + | \begin{cases} | ||
| + | ~30^\circ + 360^\circ \cdot k | ||
| + | \\ | ||
| + | 210^\circ + 360^\circ \cdot k | ||
| + | \end{cases} | ||
| + | , \, k \in \mathbb{Z}</math> | ||
| + | }} | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado={{p}} | |enunciado={{p}} | ||
| - | '''1. '''Resuelve: <math>2 \, tg \, x - 3\, cot \, x - 1=0</math> | + | '''2. '''Resuelve: <math>2 \, tg \, x - 3\, cot \, x - 1=0</math> |
| |sol= | |sol= | ||
| + | '''Solución:''' | ||
| + | {{p}} | ||
| Transformamos la ecuación de partida: | Transformamos la ecuación de partida: | ||
| Línea 35: | Línea 71: | ||
| </math> | </math> | ||
| - | :<math>\begin{cases} z_1=\cfrac{3}{2} \rightarrow tg \, x_1=\cfrac{3}{2} \rightarrow x_1 = arctg \, \cfrac{3}{2}=56^\circ \, 18' \, 35'' + 180^\circ \cdot k\\ z_2=-1 \rightarrow tg \, x_2=-1 \rightarrow x_2 = arctg \, -1=135^\circ + 180^\circ \cdot k \end{cases} \, , \quad k \in \mathbb{Z}</math> | + | Deshacemos el cambio de variable: |
| + | {{p}} | ||
| + | *<math>z_1=\cfrac{3}{2} \rightarrow tg \, x_1=\cfrac{3}{2} \rightarrow x_1 =56^\circ \, 18' \, 35'' + 180^\circ \cdot k \, , \quad k \in \mathbb{Z}</math> | ||
| + | {{p}} | ||
| + | *<math>z_2=-1 \rightarrow tg \, x_2=-1 \rightarrow x_2 =135^\circ + 180^\circ \cdot k \, , \quad k \in \mathbb{Z}</math> | ||
| '''Soluciones:''' | '''Soluciones:''' | ||
| - | :<math>\begin{cases} x_1 =56^\circ \, 18' \, 35'' + 180^\circ \cdot k\\x_2=135^\circ + 180^\circ \cdot k\end{cases} \, , \quad k \in \mathbb{Z}</math> | + | :<math>x= |
| + | \begin{cases} 56^\circ \, 18' \, 35'' + 180^\circ \cdot k | ||
| + | \\ | ||
| + | 135^\circ + 180^\circ \cdot k | ||
| + | \end{cases} | ||
| + | \, , \quad k \in \mathbb{Z}</math> | ||
| }} | }} | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | '''2. '''Resuelve: {{sube|porcentaje=+20%|contenido=<math>cos^2 \, x - 3\, sen^2 \, x =0</math>}} | + | '''3. '''Resuelve: {{sube|porcentaje=+20%|contenido=<math>cos^2 \, x - 3\, sen^2 \, x =0</math>}} |
| |sol= | |sol= | ||
| + | '''Solución:''' | ||
| + | {{p}} | ||
| Usando la identidad fundamental: | Usando la identidad fundamental: | ||
| Línea 54: | Línea 101: | ||
| :<math>1-4 \, sen^2 \, x =0 \rightarrow sen^2 \, x =\cfrac{1}{4}\rightarrow sen \, x =\pm \cfrac{1}{2}</math> | :<math>1-4 \, sen^2 \, x =0 \rightarrow sen^2 \, x =\cfrac{1}{4}\rightarrow sen \, x =\pm \cfrac{1}{2}</math> | ||
| - | '''Soluciones:''' | + | Veamos cada uno de los dos casos: |
| - | :<math>x=\begin{cases} arcsen \, \cfrac{1}{2}= | + | *<math>sen \, x = \cfrac{1}{2} \rightarrow \begin{cases} |
| - | \begin{cases} | + | |
| x_1 =30^\circ + 360^\circ \cdot k | x_1 =30^\circ + 360^\circ \cdot k | ||
| \\ | \\ | ||
| x_2 =150^\circ + 360^\circ \cdot k | x_2 =150^\circ + 360^\circ \cdot k | ||
| - | \end{cases} | + | \end{cases} |
| + | </math> | ||
| + | {{p}} | ||
| + | *<math> | ||
| + | sen \, x = -\cfrac{1}{2} \rightarrow \begin{cases} | ||
| + | x_3 =210^\circ + 360^\circ \cdot k | ||
| + | \\ | ||
| + | x_4 =330^\circ + 360^\circ \cdot k | ||
| + | \end{cases}</math> | ||
| + | '''Soluciones:''' | ||
| + | |||
| + | :<math>x=\begin{cases} | ||
| + | 30^\circ + 360^\circ \cdot k | ||
| \\ | \\ | ||
| - | arcsen \, -\cfrac{1}{2}= | + | 150^\circ + 360^\circ \cdot k |
| - | \begin{cases} | + | |
| - | x_3 =210^\circ + 360^\circ \cdot k | + | |
| \\ | \\ | ||
| - | x_4 =330^\circ + 360^\circ \cdot k | + | 210^\circ + 360^\circ \cdot k |
| + | \\ | ||
| + | 330^\circ + 360^\circ \cdot k | ||
| - | \end{cases} | + | \end{cases}</math> |
| - | x_2=135^\circ + 180^\circ \cdot k \end{cases} \, , \quad k \in \mathbb{Z}</math> | + | |
| }} | }} | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | '''3. '''Resuelve: <math>sen(2x+60^\circ)+sen(x+30^\circ)=0</math> | + | '''4. '''Resuelve: <math>cos \,3x + cos \, x=0</math> |
| |sol= | |sol= | ||
| + | '''Solución:''' | ||
| + | {{p}} | ||
| Transformamos la suma en producto: | Transformamos la suma en producto: | ||
| + | {{p}} | ||
| + | :<math>2 \cdot cos \, \cfrac{3x+x}{2} \cdot cos \, \cfrac{3x-x}{2}=0</math> | ||
| - | :<math>2 \, sen \Big( \cfrac{2x+x+60^\circ+30^\circ}{2} \Big) \cdot cos \Big( \cfrac{2x-x+60^\circ-30^\circ}{2} \Big)=0</math> | + | :<math>2 \cdot cos \, 2x \cdot cos \, x = 0</math> |
| - | :<math>2 \, sen \Big( \cfrac{3x}{2}+45^\circ \Big) \cdot cos \Big( \cfrac{x+15^\circ}{2} \Big)=0</math> | + | {{b4}} |
| Dividimos ambos miembros entre 2 e igualamos a cero cada factor: | Dividimos ambos miembros entre 2 e igualamos a cero cada factor: | ||
| - | :<math>sen \Big( \cfrac{3x}{2}+45^\circ \Big)=0 \rightarrow | + | :<math>cos \, 2x \cdot cos \, x = 0 \rightarrow |
| \begin{cases} | \begin{cases} | ||
| - | \cfrac{3x}{2}+45^\circ=0^\circ + 360^\circ \cdot k \rightarrow x_1=-30^\circ + 240^\circ \cdot k | + | cos \, 2x =0 |
| \\ | \\ | ||
| - | \cfrac{3x}{2}+45^\circ=180^\circ + 360^\circ \cdot k \rightarrow x_2=90^\circ + 240^\circ \cdot k | + | \acute{o} |
| + | \\ | ||
| + | cos \, x = 0 | ||
| - | \end{cases} \, , \quad k \in \mathbb{Z}</math> | + | \end{cases}</math> |
| - | + | {{p}} | |
| - | :<math>cos \Big( \cfrac{x}{2}+15^\circ \Big)=0 \rightarrow | + | Veamos que ocurre en cada caso: |
| + | {{p}} | ||
| + | *<math>cos \, x = 0 \rightarrow | ||
| \begin{cases} | \begin{cases} | ||
| - | \cfrac{x}{2}+15^\circ=90^\circ + 360^\circ \cdot k \rightarrow x_3=150^\circ + 720^\circ \cdot k | + | x_1=90^\circ + 360^\circ \cdot k |
| \\ | \\ | ||
| - | \cfrac{x}{2}+15^\circ=270^\circ + 360^\circ \cdot k \rightarrow x_4=510^\circ + 720^\circ \cdot k | + | x_2=270^\circ + 360^\circ \cdot k |
| \end{cases} \, , \quad k \in \mathbb{Z}</math> | \end{cases} \, , \quad k \in \mathbb{Z}</math> | ||
| + | {{b4}} | ||
| + | *<math>cos \, 2x = 0 \rightarrow cos^2 \, x - sen^2 \, x = 0 \rightarrow cos^2 \, x = sen^2 \, x </math> | ||
| + | {{p}} | ||
| + | :<math>\rightarrow | ||
| + | \begin{cases} | ||
| + | cos \, x = sen \, x \rightarrow | ||
| + | \begin{cases} | ||
| + | x_3 = 45^\circ + 360^\circ \cdot k | ||
| + | \\ | ||
| + | x_4 = 225^\circ + 360^\circ \cdot k | ||
| - | '''Soluciones:''' | + | \end{cases} \, , \quad k \in \mathbb{Z} |
| + | \\ | ||
| + | \acute{o} | ||
| + | \\ | ||
| + | cos \, x = -sen \, x \rightarrow | ||
| + | \begin{cases} | ||
| + | x_5 = 135^\circ + 360^\circ \cdot k | ||
| + | \\ | ||
| + | x_6 = 315^\circ + 360^\circ \cdot k | ||
| - | <math>x=\begin{cases} | + | \end{cases} \, , \quad k \in \mathbb{Z} |
| - | -30^\circ + 360^\circ \cdot k | + | |
| + | \end{cases}</math> | ||
| + | |||
| + | |||
| + | '''Soluciones:''' | ||
| + | Se comprueba que los 6 conjuntos de soluciones anteriores son válidos. Podemos abreviar su expresión de la siguiente manera: | ||
| + | {{p}} | ||
| + | :<math>x=\begin{cases} | ||
| + | 90^\circ + 180^\circ \cdot k | ||
| \\ | \\ | ||
| - | \, \, 150^\circ + 360^\circ \cdot k | + | 45^\circ + 90^\circ \cdot k |
| \end{cases} \, , \quad k \in \mathbb{Z}</math> | \end{cases} \, , \quad k \in \mathbb{Z}</math> | ||
| Línea 116: | Línea 207: | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | '''4. '''Resuelve: {{sube|porcentaje=15%|contenido=<math>sen^2 \, x - cos^2 \, x = \cfrac{1}{2}</math>}} | + | '''5. '''Resuelve: {{sube|porcentaje=15%|contenido=<math>sen^2 \, x - cos^2 \, x = \cfrac{1}{2}</math>}} |
| |sol= | |sol= | ||
| + | '''Solución:''' | ||
| + | {{p}} | ||
| Multiplicamos los dos miembros por -1: | Multiplicamos los dos miembros por -1: | ||
| Línea 127: | Línea 220: | ||
| 240^\circ + 360^\circ \cdot k | 240^\circ + 360^\circ \cdot k | ||
| - | \end{cases} \, , \quad k \in \mathbb{Z}</math> | + | \end{cases} \, , \ k \in \mathbb{Z} \ \rightarrow</math><math> x= |
| + | \begin{cases} | ||
| + | \, 60^\circ + 180^\circ \cdot k | ||
| + | \\ | ||
| + | 120^\circ + 180^\circ \cdot k | ||
| + | |||
| + | \end{cases} \, , \ k \in \mathbb{Z}</math> | ||
| '''Soluciones:''' | '''Soluciones:''' | ||
| - | <math>x= | + | :<math>x= |
| \begin{cases} | \begin{cases} | ||
| \, 60^\circ + 180^\circ \cdot k | \, 60^\circ + 180^\circ \cdot k | ||
| Línea 142: | Línea 241: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace | + | {{Videotutoriales|titulo=Ecuaciones trigonométricas|enunciado= |
| - | |titulo1= 3 ejercicios (Ecuaciones trigonométricas) | + | {{Video_enlace_pildoras |
| + | |titulo1=Tutorial 1a | ||
| + | |duracion=14'20" | ||
| + | |sinopsis=Ecuaciones trigonométricas. Ejemplos. | ||
| + | {{p}} | ||
| + | |url1=https://youtu.be/XhIz5xK6IeU?list=PLwCiNw1sXMSCaukmrbPRm2SQuhas4kWS_ | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1b | ||
| + | |duracion=18'21" | ||
| + | |sinopsis=Ecuaciones trigonométricas. Más ejemplos. | ||
| + | {{p}} | ||
| + | |url1=https://youtu.be/8Em5CxFV-aU?list=PLwCiNw1sXMSCaukmrbPRm2SQuhas4kWS_ | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=4´02" | ||
| + | |url1=https://www.youtube.com/watch?v=EN7S3jzkmLs | ||
| + | |sinopsis=Resuelve: <math>2 sen \, \theta \, -1 = 0\;</math> con <math>0 \le \theta < 360^o\;</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=4´25" | ||
| + | |url1=https://www.youtube.com/watch?v=TlRzT96DUYs | ||
| + | |sinopsis=Resuelve: <math>2 cos \, \alpha \, + \sqrt{3} = 0\;</math> con <math>0 \le \alpha < 360^o\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=6´11" | ||
| + | |url1=https://www.youtube.com/watch?v=1eoNHyuPKhY | ||
| + | |sinopsis=Resuelve dando la solución en radianes: <math>sen \, x = \cfrac{1}{3}\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=5´20" | ||
| + | |url1=https://www.youtube.com/watch?v=oH3V0_EUBkQ | ||
| + | |sinopsis=Resuelve dando la solución en radianes: | ||
| + | |||
| + | # <math>cos \, \theta = 1\;</math>. | ||
| + | # <math>cos \, \theta = -1\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 3a | ||
| + | |duracion=6´23" | ||
| + | |url1=https://www.youtube.com/watch?v=2Poj4GNWJ7k | ||
| + | |sinopsis=Resuelve: <math>tg^2 x + cosec^2 x \, - 3 = 0\;</math> (1ª parte) | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 3b | ||
| + | |duracion=5´58" | ||
| + | |url1=https://www.youtube.com/watch?v=gfCpZCq8MIk | ||
| + | |sinopsis=Resuelve: <math>tg^2 x + cosec^2 x \, - 3 = 0\;</math> (2ª parte) | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=6'41" | ||
| + | |sinopsis=Resuelve: <math>-3 sen \, x + cos^2 x= 3\;</math> | ||
| + | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/trigonometria/ecuaciones-trigonometricas/ecuacion-trigonometrica-01 | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=7'02" | ||
| + | |sinopsis=Resuelve el sistema: | ||
| + | |||
| + | :<math>\left . \begin{matrix} sen \, x + sen \, y =\ \cfrac{\sqrt{3} + 1}{2} \\ sen \, x - sen \, y =\ \cfrac{\sqrt{3} - 1}{2} \end{matrix} \right \}</math> | ||
| + | |||
| + | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/trigonometria/sistemas-de-ecuaciones-trigonometricas/sistema-de-ecuaciones-trigonometricas-01 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1= Ejercicio 6 | ||
| |duracion=5´55" | |duracion=5´55" | ||
| - | |url1=http://www.youtube.com/watch?v=H2K6xqAHskE | + | |url1=https://www.youtube.com/watch?v=H2K6xqAHskE&list=PL8C0D37B1235315C7&index=26 |
| - | |sinopsis=Videotutorial. | + | |sinopsis=Resuelve las siguientes ecuaciones: |
| + | *<math>1+sen \, x- cos^2 \, x =0</math> | ||
| + | *<math>cos \, x + cos \, 2x =0</math> | ||
| + | *<math>sen \, x + cos \, x =1</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace | + | {{Video_enlace_fonemato |
| - | |titulo1= 3 ejercicios (Ecuaciones trigonométricas) | + | |titulo1= Ejercicio 7 |
| |duracion=5´44" | |duracion=5´44" | ||
| - | |url1=http://www.youtube.com/watch?v=71ah85_lSWw | + | |url1=https://www.youtube.com/watch?v=71ah85_lSWw&index=27&list=PL8C0D37B1235315C7 |
| - | |sinopsis=Videotutorial. | + | |sinopsis=Resuelve las siguientes ecuaciones: |
| + | *<math>sen \, 2x = tg \, x</math> | ||
| + | *<math>sen \, x + cos \, x =sec \, x</math> | ||
| + | *<math>tg \, 2x =tg \, x</math> | ||
| + | }} | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | {{Actividades|titulo=Ecuaciones trigonométricas|enunciado= | ||
| + | {{AI_Khan | ||
| + | |descripcion=Ecuaciones trigonométricas sencillas. | ||
| + | |url1=http://es.khanacademy.org/math/trigonometry/trig-equations-and-identities/solving-sinusoidal-models/a/trigonometric-equations-review | ||
| + | |titulo1=Actividad 1 | ||
| + | }} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás practicar ejercicios sobre resolución de ecuaciones trigonométricas sencillas. | ||
| + | |enlace=[http://ggbm.at/EjaJYtcx Actividad 2] | ||
| + | }} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás practicar ejercicios sobre resolución de ecuaciones trigonométricas que se pueden factorizar. | ||
| + | |enlace=[http://ggbm.at/YM8VUvWe Actividad 3] | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |descripcion=Resuelve ecuaciones trigonométricas (básico). | ||
| + | |url1=http://es.khanacademy.org/math/trigonometry/trig-equations-and-identities/basic-sinusoidal-equations/e/solve-basic-sinusoidal-equations | ||
| + | |titulo1=Autoevaluación 1 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |descripcion=Resuelve ecuaciones trigonométricas. | ||
| + | |url1=http://es.khanacademy.org/math/trigonometry/trig-equations-and-identities/advanced-sinusoidal-equations/e/solve-advanced-sinusoidal-equations | ||
| + | |titulo1=Autoevaluación 2 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |descripcion=Problemas para resolver por medio de ecuaciones trigonométricas. | ||
| + | |url1=http://es.khanacademy.org/math/trigonometry/trig-equations-and-identities/solving-sinusoidal-models/e/inverse-trig-word-problems | ||
| + | |titulo1=Autoevaluación 3 | ||
| + | }} | ||
| + | {{AI_vitutor | ||
| + | |titulo1=Autoevaluación 4 | ||
| + | |descripcion=Ejercicios de autoevaluación sobre ecuaciones trigonométricas. | ||
| + | |url1=http://www.vitutor.com/al/trigo/e_e.html | ||
| + | }} | ||
| + | {{AI_vitutor | ||
| + | |titulo1=Autoevaluación 5 | ||
| + | |descripcion=Ejercicios de autoevaluación sobre sistemas de ecuaciones trigonométricas. | ||
| + | |url1=http://www.vitutor.com/al/trigo/s_e.html | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 191: | Línea 413: | ||
| }} | }} | ||
| - | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Funciones]] | + | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría:Álgebra]] |
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Ecuaciones trigonométricas
Una ecuación trigonométrica es aquella en la que las incógnitas aparecen formando parte de los argumentos de funciones trigonométricas.
Como las incógnitas son ángulos, si existe alguna solución, éstas van a ser infinitas (todos los ángulos coterminales con el que hallemos), pero normalmente nos bastará con dar la solución comprendida entre 0º y 360º. También puede darse la solución en radianes.
Las estrategias a seguir para resolver estas ecuaciones son muy diversas: cambio de variable, uso de identidades trigonométricas fundamentales y de fórmulas trigonométricas, etc.
Veamos algunos ejemplos:
Ejemplos: Ecuaciones trigonométricas
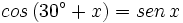
Solución:
Desarrollamos el coseno de una suma en el primer miembro:
Dividimos ambos miembros por 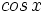 . (Observa que
. (Observa que 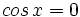 si
si 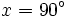 ó
ó 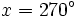 , valores que no cumplen la ecuación de partida. Por tanto no estaríamos dividiendo por cero y no perderíamos ninguna solución)
, valores que no cumplen la ecuación de partida. Por tanto no estaríamos dividiendo por cero y no perderíamos ninguna solución)
Soluciones:
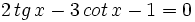
Solución:
Transformamos la ecuación de partida:
Hacemos un cambio de variable: 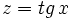
Deshacemos el cambio de variable:
Soluciones:
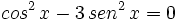
Solución:
Usando la identidad fundamental:
Sustituimos en nuestra ecuación de partida:
Veamos cada uno de los dos casos:
Soluciones:
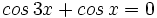
Solución:
Transformamos la suma en producto:
Dividimos ambos miembros entre 2 e igualamos a cero cada factor:
Veamos que ocurre en cada caso:
Soluciones:
Se comprueba que los 6 conjuntos de soluciones anteriores son válidos. Podemos abreviar su expresión de la siguiente manera:
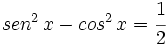
Solución:
Multiplicamos los dos miembros por -1:
Soluciones:
Ecuaciones trigonométricas. Ejemplos.
Ecuaciones trigonométricas. Más ejemplos.
Resuelve: 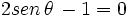 con
con 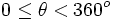
Resuelve: 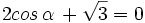 con
con 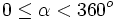
Resuelve dando la solución en radianes: 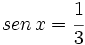 .
.
Resuelve dando la solución en radianes:
-
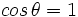 .
.
-
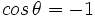 .
.
Resuelve: 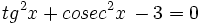 (1ª parte)
(1ª parte)
Resuelve: 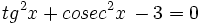 (2ª parte)
(2ª parte)
Resuelve: 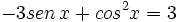
Resuelve el sistema:
Resuelve las siguientes ecuaciones:
Resuelve las siguientes ecuaciones:
Ecuaciones trigonométricas sencillas.
En esta escena podrás practicar ejercicios sobre resolución de ecuaciones trigonométricas sencillas.
En esta escena podrás practicar ejercicios sobre resolución de ecuaciones trigonométricas que se pueden factorizar.
Resuelve ecuaciones trigonométricas (básico).
Resuelve ecuaciones trigonométricas.
Problemas para resolver por medio de ecuaciones trigonométricas.
Ejercicios de autoevaluación sobre ecuaciones trigonométricas.
Ejercicios de autoevaluación sobre sistemas de ecuaciones trigonométricas.
|
Actividad: Ecuaciones trigonométricas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios propuestos
|
Ejercicios propuestos: Ecuaciones trigonométricas |