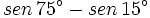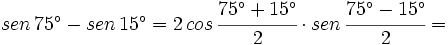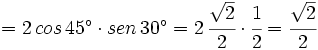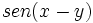Fórmulas trigonométricas (1ºBach)
De Wikipedia
| Revisión de 17:49 3 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Introducción) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Razones trigonométricas de la suma de dos ángulos== | + | ==Introducción== |
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Razones del ángulo suma, diferencia, doble y mitad | ||
| + | |duracion=13´12" | ||
| + | |url1=https://youtu.be/zYCytkWAeiI?list=PLwCiNw1sXMSCaukmrbPRm2SQuhas4kWS_ | ||
| + | |sinopsis=En este tutorial se condensan todas las fórmulas que van a verse en esta página, acompañadas de algunos ejemplos. | ||
| + | }} | ||
| + | |||
| + | ==Razones trigonométricas de la suma y de la diferencia de dos ángulos== | ||
| {{Teorema|titulo=Razones trigonométricas de la suma de dos ángulos | {{Teorema|titulo=Razones trigonométricas de la suma de dos ángulos | ||
| |enunciado= | |enunciado= | ||
| - | :'''I.1:'''{{b4}}<math>sen \, (\alpha + \beta) = sen \, \alpha \cdot cos \, \beta + cos \, \alpha \cdot sen \, \beta</math> | + | '''I.1:'''{{b4}}<math>sen \, (\alpha + \beta) = sen \, \alpha \cdot cos \, \beta + cos \, \alpha \cdot sen \, \beta</math> |
| - | + | {{p}} | |
| - | :'''I.2:'''{{b4}}<math>cos \, (\alpha + \beta) = cos \, \alpha \cdot cos \, \beta - sen \, \alpha \cdot sen \, \beta</math> | + | '''I.2:'''{{b4}}<math>cos \, (\alpha + \beta) = cos \, \alpha \cdot cos \, \beta - sen \, \alpha \cdot sen \, \beta</math> |
| - | + | {{p}} | |
| - | :'''I.3:'''{{b4}}{{sube|porcentaje=+10%|contenido=<math>tg \, (\alpha + \beta) = \frac{tg \, \alpha + tg \, \beta}{1 - tg \, \alpha \cdot tg \, \beta}</math>}} | + | '''I.3:'''{{b4}}{{sube|porcentaje=+10%|contenido=<math>tg \, (\alpha + \beta) = \frac{tg \, \alpha + tg \, \beta}{1 - tg \, \alpha \cdot tg \, \beta}</math>}} |
| |demo=[[Imagen:senosuma.png|right|250px]] | |demo=[[Imagen:senosuma.png|right|250px]] | ||
| '''I.1:''' | '''I.1:''' | ||
| - | + | {{p}} | |
| <math>sen \, (\alpha + \beta)=\cfrac{\overline{BP}}{\overline{OB}}=\cfrac{\overline{CA}+\overline{AQ}}{\overline{OB}}</math> | <math>sen \, (\alpha + \beta)=\cfrac{\overline{BP}}{\overline{OB}}=\cfrac{\overline{CA}+\overline{AQ}}{\overline{OB}}</math> | ||
| - | + | {{p}} | |
| *En el triángulo '''ABC''': <math>\overline{CA}=\overline{AB} \cdot cos \, \alpha</math> | *En el triángulo '''ABC''': <math>\overline{CA}=\overline{AB} \cdot cos \, \alpha</math> | ||
| + | {{p}} | ||
| *En el triángulo '''OAQ''': <math>\overline{AQ}=\overline{OA} \cdot sen \, \alpha</math> | *En el triángulo '''OAQ''': <math>\overline{AQ}=\overline{OA} \cdot sen \, \alpha</math> | ||
| + | {{p}} | ||
| *En el triángulo '''OBA''': <math>\begin{cases} \overline{AB}=\overline{OB} \cdot sen \, \beta \\ \overline{OA}=\overline{OB} \cdot cos \, \beta \end{cases}</math> | *En el triángulo '''OBA''': <math>\begin{cases} \overline{AB}=\overline{OB} \cdot sen \, \beta \\ \overline{OA}=\overline{OB} \cdot cos \, \beta \end{cases}</math> | ||
| - | + | {{p}} | |
| Sustituyendo: | Sustituyendo: | ||
| - | + | {{p}} | |
| <math>sen \, (\alpha + \beta)=\cfrac{\overline{BP}}{\overline{OB}}=\cfrac{\overline{CA}+\overline{AQ}}{\overline{OB}}=\cfrac{\overline{AB} \cdot cos \, \alpha +\overline{OA} \cdot sen \, \alpha}{\overline{OB}}=</math> | <math>sen \, (\alpha + \beta)=\cfrac{\overline{BP}}{\overline{OB}}=\cfrac{\overline{CA}+\overline{AQ}}{\overline{OB}}=\cfrac{\overline{AB} \cdot cos \, \alpha +\overline{OA} \cdot sen \, \alpha}{\overline{OB}}=</math> | ||
| + | {{p}} | ||
| ::::<math>=\cfrac{\overline{OB} \cdot sen \, \beta \cdot cos \, \alpha +\overline{OB} \cdot cos \, \beta \cdot sen \, \alpha}{\overline{OB}}=</math> | ::::<math>=\cfrac{\overline{OB} \cdot sen \, \beta \cdot cos \, \alpha +\overline{OB} \cdot cos \, \beta \cdot sen \, \alpha}{\overline{OB}}=</math> | ||
| + | {{p}} | ||
| ::::<math>= sen \, \beta \cdot cos \, \alpha + cos \, \beta \cdot sen \, \alpha</math> | ::::<math>= sen \, \beta \cdot cos \, \alpha + cos \, \beta \cdot sen \, \alpha</math> | ||
| - | + | {{p}} | |
| - | + | ||
| '''I.2:''' | '''I.2:''' | ||
| - | + | {{p}} | |
| <math>cos \, (\alpha + \beta)=\cfrac{\overline{OP}}{\overline{OB}}=\cfrac{\overline{OQ}-\overline{BC}}{\overline{OB}}</math> | <math>cos \, (\alpha + \beta)=\cfrac{\overline{OP}}{\overline{OB}}=\cfrac{\overline{OQ}-\overline{BC}}{\overline{OB}}</math> | ||
| - | + | {{p}} | |
| *En el triángulo '''ABC''': <math>\overline{BC}=\overline{AB} \cdot sen \, \alpha</math> | *En el triángulo '''ABC''': <math>\overline{BC}=\overline{AB} \cdot sen \, \alpha</math> | ||
| + | {{p}} | ||
| *En el triángulo '''OAQ''': <math>\overline{OQ}=\overline{OA} \cdot cos \, \alpha</math> | *En el triángulo '''OAQ''': <math>\overline{OQ}=\overline{OA} \cdot cos \, \alpha</math> | ||
| - | + | {{p}} | |
| Sustituyendo: | Sustituyendo: | ||
| - | + | {{p}} | |
| <math>cos \, (\alpha + \beta)=\cfrac{\overline{OP}}{\overline{OB}}=\cfrac{\overline{OQ}-\overline{BC}}{\overline{OB}}=\cfrac{\overline{OA} \cdot cos \, \alpha -\overline{AB} \cdot sen \, \alpha}{\overline{OB}}=</math> | <math>cos \, (\alpha + \beta)=\cfrac{\overline{OP}}{\overline{OB}}=\cfrac{\overline{OQ}-\overline{BC}}{\overline{OB}}=\cfrac{\overline{OA} \cdot cos \, \alpha -\overline{AB} \cdot sen \, \alpha}{\overline{OB}}=</math> | ||
| + | {{p}} | ||
| ::::<math>\cfrac{\overline{OB} \cdot cos \, \beta \cdot cos \, \alpha -\overline{OB} \cdot sen \, \beta \cdot sen \, \alpha}{\overline{OB}}=</math> | ::::<math>\cfrac{\overline{OB} \cdot cos \, \beta \cdot cos \, \alpha -\overline{OB} \cdot sen \, \beta \cdot sen \, \alpha}{\overline{OB}}=</math> | ||
| + | {{p}} | ||
| ::::<math>= cos \, \alpha \cdot cos \, \beta - sen \, \alpha \cdot sen \, \beta</math> | ::::<math>= cos \, \alpha \cdot cos \, \beta - sen \, \alpha \cdot sen \, \beta</math> | ||
| - | + | {{p}} | |
| '''I.3:''' | '''I.3:''' | ||
| - | + | {{p}} | |
| <math>tg \, (\alpha + \beta)=\cfrac{sen \, (\alpha + \beta)}{cos \, (\alpha + \beta)}=\cfrac{sen \, \beta \cdot cos \, \alpha + cos \, \beta \cdot sen \, \alpha}{cos \, \alpha \cdot cos \, \beta - sen \, \alpha \cdot sen \, \beta}=</math> | <math>tg \, (\alpha + \beta)=\cfrac{sen \, (\alpha + \beta)}{cos \, (\alpha + \beta)}=\cfrac{sen \, \beta \cdot cos \, \alpha + cos \, \beta \cdot sen \, \alpha}{cos \, \alpha \cdot cos \, \beta - sen \, \alpha \cdot sen \, \beta}=</math> | ||
| - | + | {{p}} | |
| ::::(Dividiendo numerador y denominador por <math>cos \, \alpha \cdot \cos \, \beta</math>) | ::::(Dividiendo numerador y denominador por <math>cos \, \alpha \cdot \cos \, \beta</math>) | ||
| - | + | {{p}} | |
| ::::<math>=\cfrac{\cfrac{sen \, \beta \cdot cos \, \alpha}{cos \, \alpha \cdot \cos \, \beta} + \cfrac{cos \, \beta \cdot sen \, \alpha}{cos \, \alpha \cdot \cos \, \beta}}{\cfrac{cos \, \alpha \cdot cos \, \beta}{cos \, \alpha \cdot \cos \, \beta} - \cfrac{sen \, \alpha \cdot sen \, \beta}{cos \, \alpha \cdot \cos \, \beta}}=\cfrac{tg \, \beta + tg \, \alpha}{1-tg \, \alpha \cdot tg \, \beta}</math> | ::::<math>=\cfrac{\cfrac{sen \, \beta \cdot cos \, \alpha}{cos \, \alpha \cdot \cos \, \beta} + \cfrac{cos \, \beta \cdot sen \, \alpha}{cos \, \alpha \cdot \cos \, \beta}}{\cfrac{cos \, \alpha \cdot cos \, \beta}{cos \, \alpha \cdot \cos \, \beta} - \cfrac{sen \, \alpha \cdot sen \, \beta}{cos \, \alpha \cdot \cos \, \beta}}=\cfrac{tg \, \beta + tg \, \alpha}{1-tg \, \alpha \cdot tg \, \beta}</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{ejemplo | ||
| + | |titulo=Ejemplo: ''Razones trigonométricas de la suma de dos ángulos'' | ||
| + | |enunciado={{p}} | ||
| + | Calcula el valor exacto de {{sube|porcentaje=15%|contenido=<math>sen \, 75^\circ \,</math>}} (sin calculadora) | ||
| + | |sol= | ||
| + | <math>sen \, 75^\circ= sen \, (45^\circ + 30^\circ)=sen \, 45^\circ \cdot cos \, 30^\circ + cos \, 45^\circ \cdot sen \, 30^\circ=</math> | ||
| + | {{p}} | ||
| + | <math>= \cfrac{\sqrt{2}}{2} \cdot \cfrac{\sqrt{3}}{2}+ \cfrac{\sqrt{2}}{2} \cdot \cfrac{1}{2}=\cfrac{\sqrt{2} \cdot (\sqrt{3}+1)}{4}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Razones trigonométricas de la suma de dos ángulos|enunciado= | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Razones trigonométricas de la suma de dos ángulos | ||
| + | |duracion=12´41 | ||
| + | |url1=https://www.youtube.com/watch?v=b1C_O92pECI&index=16&list=PL8C0D37B1235315C7 | ||
| + | |sinopsis=Fórmulas trigonométricas de la suma de dos ángulos con demostración. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Seno de la suma de dos ángulos | ||
| + | |duracion=16´12" | ||
| + | |url1=https://www.youtube.com/watch?v=Wu7cWAPm64c | ||
| + | |sinopsis=Demostración de la fórmula del seno de la suma de dos ángulos. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Coseno de la suma de dos ángulos | ||
| + | |duracion=17´52" | ||
| + | |url1=https://www.youtube.com/watch?v=KmjSkDW3ykE | ||
| + | |sinopsis=Demostración de la fórmula del coseno de la suma de dos ángulos. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Tangente de la suma de dos ángulos | ||
| + | |duracion=9´45" | ||
| + | |url1=https://www.youtube.com/watch?v=xAy-uOMXzU0 | ||
| + | |sinopsis=Demostración de la fórmula de la tangente de la suma de dos ángulos. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Seno de la suma de dos ángulos | ||
| + | |duracion=7´46" | ||
| + | |url1=https://www.youtube.com/watch?v=XFlmO483bgc | ||
| + | |sinopsis=Demostración de la fórmula del seno de la suma de dos ángulos. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Coseno de la suma de dos ángulos | ||
| + | |duracion=5´13" | ||
| + | |url1=https://www.youtube.com/watch?v=6vuXcHqerPg | ||
| + | |sinopsis=Demostración de la fórmula del coseno de la suma de dos ángulos. | ||
| + | }} | ||
| - | ==Razones trigonométricas de la diferencia de dos ángulos== | + | {{Video_enlace_abel |
| + | |titulo1=Cotangente de la suma de dos ángulos | ||
| + | |duracion=11´15" | ||
| + | |url1=https://www.youtube.com/watch?v=wZA_Iz1Vg7c | ||
| + | |sinopsis=Demostración de la fórmula de la cotangente de la suma de dos ángulos. | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Razones trigonométricas de la suma de tres ángulos | ||
| + | |duracion=5´23" | ||
| + | |url1=https://www.youtube.com/watch?v=gcto_sBqkGc&index=17&list=PL8C0D37B1235315C7 | ||
| + | |sinopsis=Obtención de la fórmula del seno, coseno y tangente de la suma de tres ángulos. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=3´15" | ||
| + | |url1=https://www.youtube.com/watch?v=0Ofgbx6Cu6E | ||
| + | |sinopsis=Halla el valor exacto de <math>cos \, 105^o</math>. | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1= Ejercicio 2 | ||
| + | |duracion=14´12" | ||
| + | |url1=https://www.youtube.com/watch?v=A8FcMRnR57E | ||
| + | |sinopsis=Halla el valor exacto de <math>tg \, 75^o</math>. | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1= Ejercicio 3 | ||
| + | |duracion=3´51" | ||
| + | |url1=https://www.youtube.com/watch?v=-jw3VsDuC6M&index=18&list=PL8C0D37B1235315C7 | ||
| + | |sinopsis=Hallar las razones trigonométricas de <math>\theta + \mu\;</math> sabiendo que <math>\theta\;</math> y <math>\mu\;</math> son del segundo cuadrante y que <math>sen \,\theta = 1/2</math> y que <math>cos \,\mu = -2/3</math>. | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1= Ejercicio 4 | ||
| + | |duracion=3´01" | ||
| + | |url1=https://www.youtube.com/watch?v=rq2v3ZyHbTM&index=19&list=PL8C0D37B1235315C7 | ||
| + | |sinopsis=Demostrar que si <math>A+B+C=180^{\circ}</math>, entonces <math>tg \, A + tg \, B + tg \, C = tg \, A \cdot tg \, B \cdot tg \, C</math>. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1= Ejercicio 5 | ||
| + | |duracion=5´45" | ||
| + | |url1=https://www.youtube.com/watch?v=XxueEKjiuuA | ||
| + | |sinopsis=Halla <math>cos\,(\hat B + 60º)</math> a partir del dibujo dado en el video. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1= Ejercicio 6 | ||
| + | |duracion=5´45" | ||
| + | |url1=https://www.youtube.com/watch?v=XxueEKjiuuA | ||
| + | |sinopsis=Halla el valor exacto de <math>sen \, \cfrac{7\pi}{12}</math>. | ||
| + | ---- | ||
| + | '''¡Ojo!:''' Estamos trabajando con ángulos en radianes. | ||
| + | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Razones trigonométricas de la suma de dos ángulos|enunciado= | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1 | ||
| + | |descripcion=Usa las identidades trigonométricas de la suma de ángulos. | ||
| + | |url1=http://es.khanacademy.org/math/trigonometry/trig-equations-and-identities/intro-to-trig-angle-addition-identities/e/trig_addition_identities | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 2 | ||
| + | |descripcion=Encuentra valores trigonométricos exactos usando las identidades de la suma de ángulos. | ||
| + | |url1=http://es.khanacademy.org/math/trigonometry/trig-equations-and-identities/using-trig-identities/e/applying-angle-addition-formulas | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| {{Teorema|titulo=Razones trigonométricas de la diferencia de dos ángulos | {{Teorema|titulo=Razones trigonométricas de la diferencia de dos ángulos | ||
| |enunciado= | |enunciado= | ||
| - | :'''II.1:'''{{b4}}<math>sen \, (\alpha - \beta) = sen \, \alpha \cdot cos \, \beta - cos \, \alpha \cdot sen \, \beta</math> | + | '''II.1:'''{{b4}}<math>sen \, (\alpha - \beta) = sen \, \alpha \cdot cos \, \beta - cos \, \alpha \cdot sen \, \beta</math> |
| - | :'''II.2:'''{{b4}}<math>cos \, (\alpha - \beta) = cos \, \alpha \cdot cos \, \beta + sen \, \alpha \cdot sen \, \beta</math> | + | '''II.2:'''{{b4}}<math>cos \, (\alpha - \beta) = cos \, \alpha \cdot cos \, \beta + sen \, \alpha \cdot sen \, \beta</math> |
| - | :'''II.3:'''{{b4}}{{sube|porcentaje=+10%|contenido=<math>tg \, (\alpha - \beta) = \frac{tg \, \alpha - tg \, \beta}{1 + tg \, \alpha \cdot tg \, \beta}</math>}} | + | '''II.3:'''{{b4}}{{sube|porcentaje=+10%|contenido=<math>tg \, (\alpha - \beta) = \frac{tg \, \alpha - tg \, \beta}{1 + tg \, \alpha \cdot tg \, \beta}</math>}} |
| |demo= | |demo= | ||
| - | Para las demostraciones basta sustituir \alpha - \beta por \alpha + (-\beta) y aplicar las fórmulas de la suma (I.1, I.2 y I.3) y tener en cuenta las relaciones entre las razones trigonométricas de un ángulo y su opuesto: | + | Para las demostraciones basta sustituir <math>\alpha - \beta \,</math> por <math>\alpha + (-\beta) \,</math> y aplicar las fórmulas de la suma ('''I.1''', '''I.2''' y '''I.3''') y tener en cuenta las relaciones entre las razones trigonométricas de un ángulo y su opuesto: |
| <center><math>sen \, (-\alpha)=-sen \, \alpha \, , \quad cos \, (-\alpha)=cos \, \alpha \, , \quad tg \, (-\alpha)=-tg \, \alpha</math></center> | <center><math>sen \, (-\alpha)=-sen \, \alpha \, , \quad cos \, (-\alpha)=cos \, \alpha \, , \quad tg \, (-\alpha)=-tg \, \alpha</math></center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Razones trigonométricas del ángulo doble== | + | {{ejemplo |
| + | |titulo=Ejemplo: ''Razones trigonométricas de la diferencia de dos ángulos'' | ||
| + | |enunciado={{p}} | ||
| + | Calcula el valor exacto de {{sube|porcentaje=15%|contenido=<math>sen \, 15^\circ</math>}} (sin calculadora) | ||
| + | |sol= | ||
| + | <math>sen \, 15^\circ= sen \, (45^\circ - 30^\circ)=sen \, 45^\circ \cdot cos \, 30^\circ - cos \, 45^\circ \cdot sen \, 30^\circ=</math> | ||
| {{p}} | {{p}} | ||
| - | ==Razones trigonométricas del ángulo mitad== | + | <math>= \cfrac{\sqrt{2}}{2} \cdot \cfrac{\sqrt{3}}{2}- \cfrac{\sqrt{2}}{2} \cdot \cfrac{1}{2}=\cfrac{\sqrt{2} \cdot (\sqrt{3}-1)}{4}</math> |
| + | }} | ||
| {{p}} | {{p}} | ||
| - | ==Sumas y diferencias de senos y cosenos== | ||
| - | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Funciones]] | + | {{Videotutoriales|titulo=Razones trigonométricas de la diferencia de dos ángulos|enunciado= |
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=7´08 | ||
| + | |url1=https://www.youtube.com/watch?v=sBpx0-KjpNA&index=20&list=PL8C0D37B1235315C7 | ||
| + | |sinopsis=Fórmulas trigonométricas de la diferencia de dos ángulos con demostración. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=3´49" | ||
| + | |url1=https://www.youtube.com/watch?v=-WnHUiePogg | ||
| + | |sinopsis=Obtención del valor exacto de <math>sen \, 15^{\circ}</math> a partir de la fórmula del seno del ángulo diferencia. | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=9´55" | ||
| + | |url1=https://www.youtube.com/watch?v=i0PZwglONQQ | ||
| + | |sinopsis=Obtención del valor exacto de <math>cos \left( arc\,sen \cfrac{8}{17} - arc\,cos \cfrac{12}{13} \right)</math>. | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Razones trigonométricas del ángulo doble y del ángulo mitad== | ||
| + | {{Teorema|titulo=Razones trigonométricas del ángulo doble | ||
| + | |enunciado= | ||
| + | '''III.1:'''{{b4}}<math>sen \, (2 \, \alpha) = 2 \, sen \, \alpha \cdot cos \, \alpha</math> | ||
| + | |||
| + | '''III.2:'''{{b4}}<math>cos \, (2 \, \alpha) = cos^2 \, \alpha - sen^2 \, \alpha</math> | ||
| + | |||
| + | '''III.3:'''{{b4}}{{sube|porcentaje=+10%|contenido=<math>tg \, (2 \, \alpha) = \frac{2 \, tg \, \alpha}{1 - tg^2 \, \alpha}</math>}} | ||
| + | |demo= | ||
| + | Basta utilizar las fórmulas de la suma ('''I.1''', '''I.2''' y '''I.3''') y hacer <math>\alpha= \beta \,</math>. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{ejemplo | ||
| + | |titulo=Ejemplo: ''Razones trigonométricas del ángulo doble'' | ||
| + | |enunciado={{p}} | ||
| + | Calcula el valor de {{sube|porcentaje=15%|contenido=<math>cos \, 120^\circ \,</math>}} a partir de las razones trigonométricas de 60º. | ||
| + | |sol= | ||
| + | <math>cos \, 120^\circ= cos^2 \, 60^\circ - sen^2 \, 60^\circ=\cfrac{1}{4}-\cfrac{3}{4}=-\cfrac{1}{2}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | {{Teorema|titulo=Razones trigonométricas del ángulo mitad | ||
| + | |enunciado= | ||
| + | '''IV.1:'''{{b4}}<math>sen \, \Big( \cfrac{\alpha}{2} \Big) = \pm \sqrt{\cfrac{1-cos \, \alpha}{2}}</math> | ||
| + | |||
| + | '''IV.2:'''{{b4}}<math>cos \, \Big( \cfrac{\alpha}{2} \Big) = \pm \sqrt{\cfrac{1+cos \, \alpha}{2}}</math> | ||
| + | |||
| + | '''IV.3:'''{{b4}}<math>tg \, \Big( \cfrac{\alpha}{2} \Big) = \pm \sqrt{\cfrac{1-cos \, \alpha}{1+cos \, \alpha}}</math> | ||
| + | |demo=Teniendo en cuenta que <math>\alpha= 2 \cdot \cfrac{\alpha}{2}</math> y utilizando la fórmula '''III.2''' del coseno del ángulo doble, tenemos: | ||
| + | |||
| + | <center><math>cos \, \alpha=cos \, \Big( 2 \cdot \cfrac{\alpha}{2} \Big) = cos^2 \, \cfrac{\alpha}{2}- sen^2 \cfrac{\alpha}{2}</math></center> | ||
| + | |||
| + | que combinado con la fórmula fundamental, nos da el siguiente sistema: | ||
| + | |||
| + | <math> | ||
| + | \begin{cases} cos \, \alpha = cos^2 \cfrac{\alpha}{2} - sen^2 \cfrac{\alpha}{2} \\ 1= cos^2 \cfrac{\alpha}{2} + sen^2 \cfrac{\alpha}{2} \end{cases} | ||
| + | </math> | ||
| + | |||
| + | Sumando y restando ambas ecuaciones, tenemos las siguientes expresiones: | ||
| + | |||
| + | <math> | ||
| + | \begin{cases} 1 + cos \, \alpha = 2 \, cos^2 \cfrac{\alpha}{2} \\ 1 - cos \, \alpha = 2 \, sen^2 \cfrac{\alpha}{2}\end{cases} | ||
| + | </math> | ||
| + | |||
| + | De estas igualdades se despejan <math>cos \, \cfrac{\alpha}{2}</math> y <math>sen \, \cfrac{\alpha}{2}</math>, y a partir de ellos, se obtiene el valor de <math>tg \, \cfrac{\alpha}{2}</math>. | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | {{ejemplo | ||
| + | |titulo=Ejemplo: ''Razones trigonométricas del ángulo mitad'' | ||
| + | |enunciado={{p}} | ||
| + | Calcula el valor exacto de {{sube|porcentaje=10%|contenido=<math>tg \, 22^\circ \, 30'</math>}} (sin calculadora). | ||
| + | |sol= | ||
| + | <math>tg \, 22^\circ \, 30'= tg \Big( \cfrac{45^\circ}{2} \Big)=\sqrt{\cfrac{1-cos \, 45^\circ}{1+cos \, 45^\circ}}=\sqrt{\cfrac{1-\cfrac{\sqrt{2}}{2}}{1+\cfrac{\sqrt{2}}{2}}}=\cfrac{\sqrt{2-\sqrt{2}}}{\sqrt{2+\sqrt{2}}}=-1+\sqrt{2}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | {{Videotutoriales|titulo=Razones trigonométricas del ángulo doble y el ángulo mitad|enunciado= | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Razones trigonométricas del ángulo doble y el ángulo mitad | ||
| + | |duracion=8´03 | ||
| + | |url1=https://www.youtube.com/watch?v=yVW2LHijBNM&index=22&list=PL8C0D37B1235315C7 | ||
| + | |sinopsis=Fórmulas trigonométricas del ángulo doble y del ángulo mitad con demostración. | ||
| + | }} | ||
| + | ---- | ||
| + | '''Razones trigonométricas del ángulo doble:''' | ||
| + | |||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Seno del ángulo doble | ||
| + | |duracion=3´00 | ||
| + | |url1=https://www.youtube.com/watch?v=npnQ54FRPV4 | ||
| + | |sinopsis=Demostración de la fórmula del seno del ángulo doble. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Coseno del ángulo doble | ||
| + | |duracion=10´42 | ||
| + | |url1=https://www.youtube.com/watch?v=eEJ_Q-Twqcg | ||
| + | |sinopsis=Demostración de la fórmula del coseno del ángulo doble. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Tangente y cotangente del ángulo doble | ||
| + | |duracion=9´19 | ||
| + | |url1=https://www.youtube.com/watch?v=h2MEjBaT-7w | ||
| + | |sinopsis=Demostración de la fórmula de la tangente y la cotangente del ángulo doble. | ||
| + | }} | ||
| + | ---- | ||
| + | |||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1= Ejercicio 1 | ||
| + | |duracion=7´04" | ||
| + | |url1=https://www.youtube.com/watch?v=BJVxcEThHp4 | ||
| + | |sinopsis=Si <math>tan \, \alpha = \cfrac{4}{3}</math> y <math>\alpha \in III</math>, halla el valor exacto de <math>sen \, 2\alpha</math>. | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=2´48" | ||
| + | |url1=https://www.youtube.com/watch?v=8ESRmd-i_qs | ||
| + | |sinopsis=Comprueba la siguiente identidad trigonométrica: | ||
| + | |||
| + | <math>4 \,sen^2 \alpha \cdot cos^2 \alpha = 1 - cos^2 (2\alpha)\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=13´46" | ||
| + | |url1=https://www.youtube.com/watch?v=sOfb8x5_9jM&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=42 | ||
| + | |sinopsis= | ||
| + | :a) Calcula: <math>sec \, 120^{\circ}</math> | ||
| + | |||
| + | :b) Sin usar la fórmula del ángulo doble, demuestra que <math>cos \, 2x = 1- sen^2 \, x</math>. | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=14´04" | ||
| + | |url1=https://www.youtube.com/watch?v=qHXaptv7Hgc&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=43 | ||
| + | |sinopsis=Halla el valor de ''x'' en la figura dada. | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=16´36" | ||
| + | |url1=https://www.youtube.com/watch?v=9knwfcegQ8o&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=44 | ||
| + | |sinopsis=Halla el valor que te piden en la figura dada. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1= Ejercicio 6 | ||
| + | |duracion=4´06" | ||
| + | |url1=https://www.youtube.com/watch?v=RdsPF0aJdCo | ||
| + | |sinopsis=Halla <math>cos\,(2\,\hat B)</math> a partir del dibujo dado en el video. | ||
| + | }} | ||
| + | ---- | ||
| + | '''Razones trigonométricas del ángulo mitad:''' | ||
| + | |||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Seno del ángulo mitad | ||
| + | |duracion=7´23 | ||
| + | |url1=https://www.youtube.com/watch?v=56-0L7bwaH8 | ||
| + | |sinopsis=Demostración de la fórmula del seno del ángulo mitad. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Coseno del ángulo mitad | ||
| + | |duracion=7´33 | ||
| + | |url1=https://www.youtube.com/watch?v=mkVb4zYb6bE | ||
| + | |sinopsis=Demostración de la fórmula del coseno del ángulo mitad. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Tangente del ángulo mitad | ||
| + | |duracion=7´40 | ||
| + | |url1=https://www.youtube.com/watch?v=OOFahCF09RU | ||
| + | |sinopsis=Demostración de la fórmula de la tangente del ángulo mitad. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=14´29" | ||
| + | |url1=https://www.youtube.com/watch?v=lIpmDO_pdBg&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=47 | ||
| + | |sinopsis= | ||
| + | :a) Demostrar que <math>tg\,\cfrac{x}{2}=cosec\,x-cotg\,x</math>. | ||
| + | |||
| + | :b) Demostrar que <math>cotg\,\cfrac{x}{2}=cosec\,x+cotg\,x</math>. (este ejercicio queda propuesto pero no resuelto) | ||
| + | |||
| + | :c) Apoyándote en los apartados anteriores, simplifica <math>M=\cfrac{cotg\, \cfrac{x}{2}-2\,cotg\,x}{tg\, \cfrac{x}{2}+cotg\,x}+cos\,x</math> | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=8´59" | ||
| + | |url1=https://www.youtube.com/watch?v=C-60bamV32A&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=45 | ||
| + | |sinopsis=Reduce <math>(cos\,a-cos\,b)^2+(sen\,a-sen\,b)^2</math> en función de <math>\cfrac{a-b}{2}</math>. | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Razones trigonométricas del ángulo triple== | ||
| + | {{Videotutoriales|titulo=Razones trigonométricas del ángulo triple|enunciado= | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1= Seno del ángulo triple | ||
| + | |duracion=13´29" | ||
| + | |url1=https://www.youtube.com/watch?v=e4lGMXfF8kQ | ||
| + | |sinopsis=Obtención de la fórmula del seno del ángulo triple. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1= Coseno del ángulo triple | ||
| + | |duracion=15´18" | ||
| + | |url1=https://www.youtube.com/watch?v=MpD0kfDgEvY | ||
| + | |sinopsis=Obtención de la fórmula del coseno del ángulo triple. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1= Tangente del ángulo triple | ||
| + | |duracion=17´44" | ||
| + | |url1=https://www.youtube.com/watch?v=Xm_qy86ZHaE | ||
| + | |sinopsis=Obtención de la fórmula de la tangente del ángulo triple. | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Seno y coseno del ángulo triple | ||
| + | |duracion=5´22" | ||
| + | |url1=https://www.youtube.com/watch?v=9TvJGhKyrVs&index=23&list=PL8C0D37B1235315C7 | ||
| + | |sinopsis=*Determinar el <math>sen 3\theta\;</math> en función del <math>sen \theta\;</math>. | ||
| + | *Determinar el <math>cos 3\theta\;</math> en función del <math>cos \theta\;</math>. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 1 | ||
| + | |duracion=6´43" | ||
| + | |url1=https://www.youtube.com/watch?v=nPXYNsTPohQ&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=49&t=11m39s | ||
| + | |sinopsis= Si <math>tg \, x + cotg \, x =6</math>, halla <math>sen\,6x</math>. | ||
| + | |||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 2 | ||
| + | |duracion=12´30" | ||
| + | |url1=https://www.youtube.com/watch?v=XCnp0TJ3V4w&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=50 | ||
| + | |sinopsis=Eliminar ''x'' en: | ||
| + | |||
| + | :<math>\left . \begin{matrix} ~cos \, x - sen \, x \ =\ a \\ cos \, 3x + sen \, 3x =\ b \end{matrix} \right \}</math> | ||
| + | |||
| + | }} | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Transformaciones de sumas y diferencias de senos y cosenos en productos== | ||
| + | {{Teorema|titulo=Transformaciones de sumas en productos | ||
| + | |enunciado= | ||
| + | '''V.1:'''{{b4}}<math>sen \, A + sen \, B = 2 \, sen \, \cfrac{A+B}{2} \cdot cos \, \cfrac{A-B}{2}</math> | ||
| + | |||
| + | '''V.2:'''{{b4}}<math>sen \, A - sen \, B = 2 \, cos \, \cfrac{A+B}{2} \cdot sen \, \cfrac{A-B}{2}</math> | ||
| + | |||
| + | '''V.3:'''{{b4}}<math>cos \, A + cos \, B = 2 \, cos \, \cfrac{A+B}{2} \cdot cos \, \cfrac{A-B}{2}</math> | ||
| + | |||
| + | '''V.4:'''{{b4}}<math>cos \, A - cos \, B = -2 \, sen \, \cfrac{A+B}{2} \cdot sen \, \cfrac{A-B}{2}</math> | ||
| + | |demo= | ||
| + | '''V.1 y V.2:''' | ||
| + | |||
| + | Partiendo de las expresiones del '''I.1''' y '''II.1''' del seno de una suma y de una diferencia: | ||
| + | |||
| + | :'''I.1:''' <math>sen \, (\alpha + \beta) = sen \, \alpha \cdot cos \, \beta + cos \, \alpha \cdot sen \, \beta</math> | ||
| + | |||
| + | :'''II.1:''' <math>sen \, (\alpha - \beta) = sen \, \alpha \cdot cos \, \beta - cos \, \alpha \cdot sen \, \beta</math> | ||
| + | |||
| + | Sumando y restando ambas expresiones, obtenemos: | ||
| + | |||
| + | :Sumando: <math>sen \, (\alpha + \beta) +sen \, (\alpha - \beta)= 2 \, sen \, \alpha \cdot cos \, \beta</math> '''[1]''' | ||
| + | |||
| + | :Restando: <math>sen \, (\alpha + \beta) -sen \, (\alpha - \beta)= 2 \, cos \, \alpha \cdot sen \, \beta</math> '''[2]''' | ||
| + | |||
| + | Hacemos los siguientes cambios de variable: | ||
| + | <math> | ||
| + | \begin{cases} \alpha + \beta = A \\ \alpha - \beta = B \end{cases} | ||
| + | </math> | ||
| + | |||
| + | Resolviendo este sistema: | ||
| + | |||
| + | <math> | ||
| + | \begin{cases} \alpha = \cfrac{A+B}{2} \\ \beta = \cfrac{A-B}{2} \end{cases} | ||
| + | </math> | ||
| + | |||
| + | que sustituidas en '''[1]''' y '''[2]''' nos da '''V.1''' y '''V.2'''. | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Transformaciones de sumas y diferencias de senos y cosenos en productos|enunciado= | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Transformación de una suma y de una diferencia en un producto | ||
| + | |duracion=6´46 | ||
| + | |url1=https://www.youtube.com/watch?v=f0W9R_ddEW8&index=28&list=PL8C0D37B1235315C7 | ||
| + | |sinopsis=Fórmulas trigonométricas de la transformación de la suma o diferencia en producto con demostración. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Transformación de una suma y de una diferencia de cosenos en un producto | ||
| + | |duracion=13´46 | ||
| + | |url1=https://www.youtube.com/watch?v=YSAnzLe153Q | ||
| + | |sinopsis=Demostración de las fórmulas trigonométricas de la transformación de la suma o diferencia de cosenos en producto. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Transformación de una suma y de una diferencia de senos en un producto | ||
| + | |duracion=13´00 | ||
| + | |url1=https://www.youtube.com/watch?v=3HBUDjB2mMA | ||
| + | |sinopsis=Demostración de las fórmulas trigonométricas de la transformación de la suma o diferencia de senos en producto. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 1 | ||
| + | |duracion=9´49 | ||
| + | |url1=https://www.youtube.com/watch?v=KfFjbB55upk&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=51 | ||
| + | |sinopsis=Ejercicios. | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 2 | ||
| + | |duracion=16´08 | ||
| + | |url1=https://www.youtube.com/watch?v=NFQBqyTkIaM&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=52 | ||
| + | |sinopsis=Ejercicios. | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 3 | ||
| + | |duracion=17´29 | ||
| + | |url1=https://www.youtube.com/watch?v=Gl3yKDXc194&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=53 | ||
| + | |sinopsis=Ejercicios. | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 4 | ||
| + | |duracion=11´04 | ||
| + | |url1=https://www.youtube.com/watch?v=uHpRYiNGudA&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=54 | ||
| + | |sinopsis=Ejercicios. | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 5 | ||
| + | |duracion=20´29 | ||
| + | |url1=https://www.youtube.com/watch?v=9BQloU-YYE0&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=55 | ||
| + | |sinopsis=Ejercicios. | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 6 | ||
| + | |duracion=17´09 | ||
| + | |url1=https://www.youtube.com/watch?v=cE3s0dugIJg&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=56 | ||
| + | |sinopsis=Ejercicios. | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{ejemplo | ||
| + | |titulo=Ejemplo: ''Transformaciones de sumas en productos'' | ||
| + | |enunciado={{p}} | ||
| + | Transforma en producto y calcula: {{sube|porcentaje=10%|contenido=<math>sen \, 75^\circ -sen \, 15^\circ</math>}}. | ||
| + | |sol= | ||
| + | <math>sen \, 75^\circ -sen \, 15^\circ= 2 \, cos \, \cfrac{75^\circ+15^\circ}{2} \cdot sen \, \cfrac{75^\circ-15^\circ}{2}= </math> | ||
| + | {{p}} | ||
| + | <math>= 2 \, cos \, 45^\circ \cdot sen \, 30^\circ= 2 \, \cfrac{\sqrt{2}}{2}\cdot \cfrac{1}{2}=\cfrac{\sqrt{2}}{2}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Fórmulas trigonométricas|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Fórmulas trigonométricas | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | :a) Calcula: {{sube|porcentaje=10%|contenido=<math>sen \, 75^\circ -sen \, 15^\circ</math>}} | ||
| + | :b) Obtén: {{sube|porcentaje=10%|contenido=<math>sen(x-y)\,</math>}} | ||
| + | :c) Factoriza: {{sube|porcentaje=10%|contenido=<math>sen(x)+sen(y)\,</math>}} | ||
| + | |||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=simplify sin(75º)-sin(15º)}} | ||
| + | :b) {{consulta|texto=expand sin(x-y)}} | ||
| + | :c) {{consulta|texto=factor sin(x)+sin(y)}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | ==Ejercicios== | ||
| + | {{AI_upr | ||
| + | |titulo1=Razones trigonométricas de la suma y de la diferencia | ||
| + | |descripcion=Actividad para practicar el cálculo de las razones trigonométricas de la suma y de la diferencia de ángulos. | ||
| + | ---- | ||
| + | '''Aviso:''' Antes de hacer la actividad puedes ver algunos ejemplos en: '''[http://quiz.uprm.edu/tutorials_master//trig_sum_dif/trig_sum_dif.html Ejemplos]''' | ||
| + | |url1=http://quiz.uprm.edu/cgi-bin/Quiz/oneques.cgi?database=Precalculo2_soluciones/trig_ids/addition-ids.db&no_ques=4 | ||
| + | }} | ||
| + | {{AI_upr | ||
| + | |titulo1=Razones trigonométricas del ángulo doble y mitad | ||
| + | |descripcion=Actividad para practicar el cálculo de las razones trigonométricas del ángulo doble y mitad. | ||
| + | ---- | ||
| + | '''Aviso:''' Antes de hacer la actividad puedes ver algunos ejemplos en: '''[http://quiz.uprm.edu/tutorials_master/trig_dob_med/trig_doble_mitad.html Ejemplos]''' | ||
| + | |||
| + | |url1=http://quiz.uprm.edu/cgi-bin/Quiz/oneques.cgi?database=Precalculo2_soluciones/trig_ids/halfang.db&no_ques=8 | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Ejercicios|enunciado= | ||
| + | '''Razones trigonométricas del ángulo suma y diferencia:''' | ||
| + | |||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 1 | ||
| + | |duracion=16'13" | ||
| + | |sinopsis=Usando las razones trigonométricas de la suma y de la diferencia, calcula: | ||
| + | |||
| + | :a) <math>cos \, 75^{\circ}</math> | ||
| + | |||
| + | :b) Si <math>tg \, (x+y)=5</math> y <math>tg \, x=7</math>, calcula <math>tg\, y</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=Fb9vpVdOmXg&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=39 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 2 | ||
| + | |duracion=14'44" | ||
| + | |sinopsis= | ||
| + | :a) Si <math>x+y=45^{\circ}\;</math>, simplifica <math>M=\cfrac{1 + tg\,x}{1 + tg\,y}</math> | ||
| + | |||
| + | :b) Simplifica: <math>M=sen \, (x+y) \cdot sen \, (x-y) + sen^2 \, y</math> | ||
| + | |url1=https://www.youtube.com/watch?v=meth8PkW5yM&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=40 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 3 | ||
| + | |duracion=11´40" | ||
| + | |url1=https://www.youtube.com/watch?v=nPXYNsTPohQ&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=49 | ||
| + | |sinopsis=Simplifica: <math>4 \, cos \, x \cdot cos \, (60^{\circ}+x) \cdot cos \, (60^{\circ}-x)</math> | ||
| + | |||
| + | }} | ||
| + | ---- | ||
| + | '''Razones trigonométricas del ángulo doble y mitad:''' | ||
| + | |||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1= Ejercicio 1 | ||
| + | |duracion=4´58" | ||
| + | |url1=https://www.youtube.com/watch?v=r4ANdw_njZc&index=24&list=PL8C0D37B1235315C7 | ||
| + | |sinopsis=Si <math>\mu</math> es un ángulo del tercer cuadrante, y <math>tg \mu = 3\;</math>, determinar las razones trigonométricas de <math>\mu /2</math>. | ||
| + | }} | ||
| + | }} | ||
| + | ===Ejercicios propuestos=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Fórmulas trigonométricas'' | ||
| + | |cuerpo= | ||
| + | (Pág. 130-133) | ||
| + | |||
| + | [[Imagen:red_star.png|12px]] 5, 7, 9, 11, 14, 15, 17b,c, 18 | ||
| + | |||
| + | [[Imagen:yellow_star.png|12px]] 1, 2, 3, 4, 6, 8, 12, 13 | ||
| + | }} | ||
| + | |||
| + | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Introducción
En este tutorial se condensan todas las fórmulas que van a verse en esta página, acompañadas de algunos ejemplos.
Razones trigonométricas de la suma y de la diferencia de dos ángulos
Razones trigonométricas de la suma de dos ángulos
I.1: 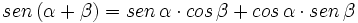
I.2: 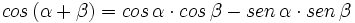
I.3: 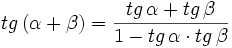
Ejemplo: Razones trigonométricas de la suma de dos ángulos
Calcula el valor exacto de 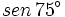 (sin calculadora)
(sin calculadora)
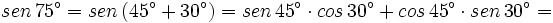
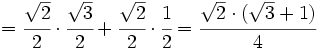
Fórmulas trigonométricas de la suma de dos ángulos con demostración.
Demostración de la fórmula del seno de la suma de dos ángulos.
Demostración de la fórmula del coseno de la suma de dos ángulos.
Demostración de la fórmula de la tangente de la suma de dos ángulos.
Demostración de la fórmula del seno de la suma de dos ángulos.
Demostración de la fórmula del coseno de la suma de dos ángulos.
Demostración de la fórmula de la cotangente de la suma de dos ángulos.
Obtención de la fórmula del seno, coseno y tangente de la suma de tres ángulos.
Halla el valor exacto de 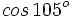 .
.
Halla el valor exacto de 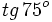 .
.
Hallar las razones trigonométricas de 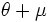 sabiendo que
sabiendo que 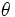 y
y 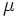 son del segundo cuadrante y que
son del segundo cuadrante y que 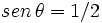 y que
y que 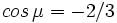 .
.
Demostrar que si 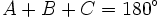 , entonces
, entonces 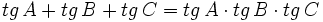 .
.
Halla 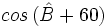 a partir del dibujo dado en el video.
a partir del dibujo dado en el video.
Halla el valor exacto de 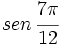 .
.
¡Ojo!: Estamos trabajando con ángulos en radianes.
Usa las identidades trigonométricas de la suma de ángulos.
Encuentra valores trigonométricos exactos usando las identidades de la suma de ángulos.
Razones trigonométricas de la diferencia de dos ángulos
II.1: 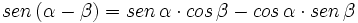
II.2: 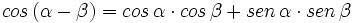
II.3: 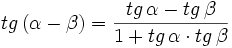
Para las demostraciones basta sustituir 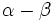 por
por 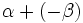 y aplicar las fórmulas de la suma (I.1, I.2 y I.3) y tener en cuenta las relaciones entre las razones trigonométricas de un ángulo y su opuesto:
y aplicar las fórmulas de la suma (I.1, I.2 y I.3) y tener en cuenta las relaciones entre las razones trigonométricas de un ángulo y su opuesto:
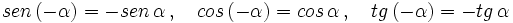
Ejemplo: Razones trigonométricas de la diferencia de dos ángulos
Calcula el valor exacto de 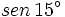 (sin calculadora)
(sin calculadora)
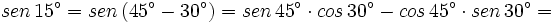
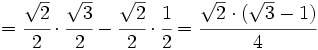
Fórmulas trigonométricas de la diferencia de dos ángulos con demostración.
Obtención del valor exacto de 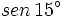 a partir de la fórmula del seno del ángulo diferencia.
a partir de la fórmula del seno del ángulo diferencia.
Obtención del valor exacto de 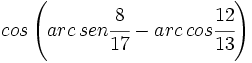 .
.
Razones trigonométricas del ángulo doble y del ángulo mitad
Razones trigonométricas del ángulo doble
III.1: 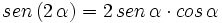
III.2: 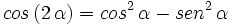
III.3: 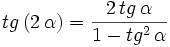
Basta utilizar las fórmulas de la suma (I.1, I.2 y I.3) y hacer
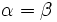 .
.Ejemplo: Razones trigonométricas del ángulo doble
Calcula el valor de 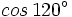 a partir de las razones trigonométricas de 60º.
a partir de las razones trigonométricas de 60º.
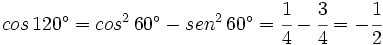
Razones trigonométricas del ángulo mitad
IV.1: 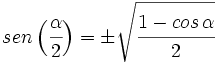
IV.2: 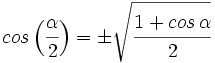
IV.3: 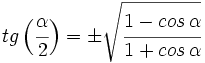
Teniendo en cuenta que 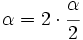 y utilizando la fórmula III.2 del coseno del ángulo doble, tenemos:
y utilizando la fórmula III.2 del coseno del ángulo doble, tenemos:
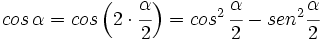
que combinado con la fórmula fundamental, nos da el siguiente sistema:
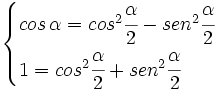
Sumando y restando ambas ecuaciones, tenemos las siguientes expresiones:
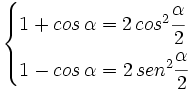
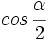 y
y 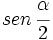 , y a partir de ellos, se obtiene el valor de
, y a partir de ellos, se obtiene el valor de 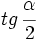 .
.Ejemplo: Razones trigonométricas del ángulo mitad
Calcula el valor exacto de 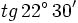 (sin calculadora).
(sin calculadora).
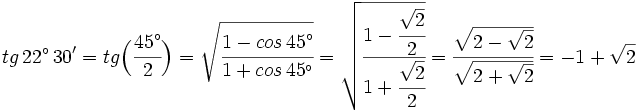
Fórmulas trigonométricas del ángulo doble y del ángulo mitad con demostración.
Razones trigonométricas del ángulo doble:
Demostración de la fórmula del seno del ángulo doble.
Demostración de la fórmula del coseno del ángulo doble.
Demostración de la fórmula de la tangente y la cotangente del ángulo doble.
Si 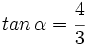 y
y 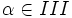 , halla el valor exacto de
, halla el valor exacto de 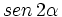 .
.
Comprueba la siguiente identidad trigonométrica:
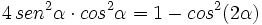
- a) Calcula:
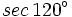
- b) Sin usar la fórmula del ángulo doble, demuestra que
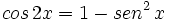 .
.
Halla el valor de x en la figura dada.
Halla el valor que te piden en la figura dada.
Halla 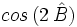 a partir del dibujo dado en el video.
a partir del dibujo dado en el video.
Razones trigonométricas del ángulo mitad:
Demostración de la fórmula del seno del ángulo mitad.
Demostración de la fórmula del coseno del ángulo mitad.
Demostración de la fórmula de la tangente del ángulo mitad.
- a) Demostrar que
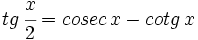 .
.
- b) Demostrar que
 . (este ejercicio queda propuesto pero no resuelto)
. (este ejercicio queda propuesto pero no resuelto)
- c) Apoyándote en los apartados anteriores, simplifica
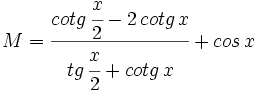
Reduce 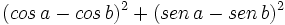 en función de
en función de 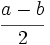 .
.
Razones trigonométricas del ángulo triple
Obtención de la fórmula del seno del ángulo triple.
Obtención de la fórmula del coseno del ángulo triple.
Obtención de la fórmula de la tangente del ángulo triple.
- Determinar el
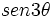 en función del
en función del 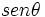 .
.
- Determinar el
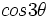 en función del
en función del 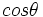 .
.
Si 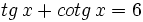 , halla
, halla 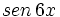 .
.
Eliminar x en:
Transformaciones de sumas y diferencias de senos y cosenos en productos
Transformaciones de sumas en productos
V.1: 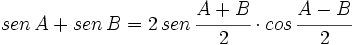
V.2: 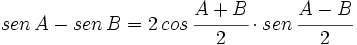
V.3: 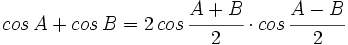
V.4: 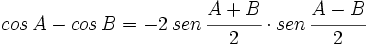
V.1 y V.2:
Partiendo de las expresiones del I.1 y II.1 del seno de una suma y de una diferencia:
- I.1:
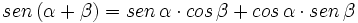
- II.1:
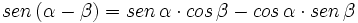
Sumando y restando ambas expresiones, obtenemos:
- Sumando:
 [1]
[1]
- Restando:
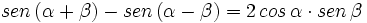 [2]
[2]
Hacemos los siguientes cambios de variable:

Resolviendo este sistema:
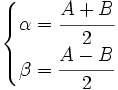
Fórmulas trigonométricas de la transformación de la suma o diferencia en producto con demostración.
Demostración de las fórmulas trigonométricas de la transformación de la suma o diferencia de cosenos en producto.
Demostración de las fórmulas trigonométricas de la transformación de la suma o diferencia de senos en producto.
Ejercicios.
Ejercicios.
Ejercicios.
Ejercicios.
Ejercicios.
Ejercicios.
Ejercicios
Actividad para practicar el cálculo de las razones trigonométricas de la suma y de la diferencia de ángulos.
Aviso: Antes de hacer la actividad puedes ver algunos ejemplos en: Ejemplos
Actividad para practicar el cálculo de las razones trigonométricas del ángulo doble y mitad.
Aviso: Antes de hacer la actividad puedes ver algunos ejemplos en: Ejemplos
Razones trigonométricas del ángulo suma y diferencia:
Usando las razones trigonométricas de la suma y de la diferencia, calcula:
- a)
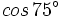
- b) Si
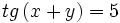 y
y 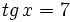 , calcula
, calcula 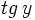 .
.
- a) Si
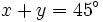 , simplifica
, simplifica 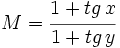
- b) Simplifica:
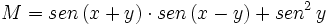
Simplifica: 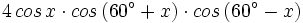
Razones trigonométricas del ángulo doble y mitad:
Si μ es un ángulo del tercer cuadrante, y 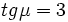 , determinar las razones trigonométricas de μ / 2.
, determinar las razones trigonométricas de μ / 2.
Ejercicios propuestos
|
Ejercicios propuestos: Fórmulas trigonométricas |
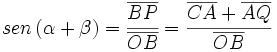
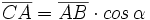
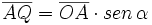
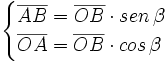
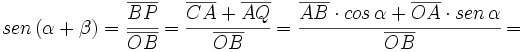
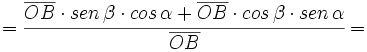
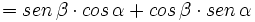
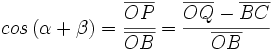
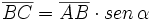
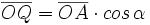
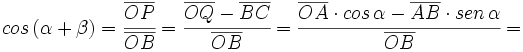
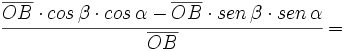
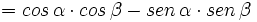
 )
)