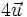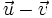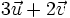Vectores: Coordenadas (1ºBach)
De Wikipedia
| Revisión de 09:59 6 feb 2018 Coordinador (Discusión | contribuciones) (→Base canónica de los vectores del plano) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Base de vectores en el plano) |
||
| Línea 8: | Línea 8: | ||
| {{p}} | {{p}} | ||
| (Pág. 174) | (Pág. 174) | ||
| + | ==Introducción== | ||
| + | Veamos unos vídeos introductorios para poder comprender mejor el concepto de base. | ||
| + | {{p}} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Dependencia e independencia lineal de vectores I | ||
| + | |duracion=13´47" | ||
| + | |url1=https://youtu.be/JRPxZMOr-NI?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Dependencia e independencia lineal de vectores. Ejemplos. Combinación lineal de vectores linealmente independientes. | ||
| + | }} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Dependencia e independencia lineal de vectores II | ||
| + | |duracion=13´47" | ||
| + | |url1=https://youtu.be/dmkWSQmim1g?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Dependencia e independencia lineal de vectores. En el plano más de dos vectores son siempre linealmente dependientes. | ||
| + | }} | ||
| ==Base de vectores en el plano== | ==Base de vectores en el plano== | ||
| - | {{Teorema|titulo=Proposición|enunciado=*Dados dos vectores {{sube|porcentaje=+30%|contenido=<math>\vec{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\vec{y}</math>}}, con distintas direcciones, cualquier vector del plano, {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}}, se puede poner como combinación lineal de ellos: | + | {{Teorema|titulo=Proposición|enunciado=*Dados dos vectores {{sube|porcentaje=+30%|contenido=<math>\vec{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\vec{y}</math>}}, con distintas direcciones (linealmente independientes), cualquier vector del plano, {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}}, se puede poner como combinación lineal de ellos: |
| {{p}} | {{p}} | ||
| <center><math>\vec{v}=a \vec{x}+b \vec{y}</math></center> | <center><math>\vec{v}=a \vec{x}+b \vec{y}</math></center> | ||
| Línea 61: | Línea 76: | ||
| Estos resultados permiten dar la siguiente definición: | Estos resultados permiten dar la siguiente definición: | ||
| {{p}} | {{p}} | ||
| - | {{Caja_Amarilla|texto=Se llama '''base''' de un conjunto de vectores del plano a dos vectores {{sube|porcentaje=+30%|contenido=<math>\vec{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\vec{y}</math>}}, con distintas direcciones. La representaremos por {{sube|porcentaje=+10%|contenido=<math>B(\vec{x},\vec{y})</math>}}. | + | {{Caja_Amarilla|texto=Se llama '''base''' de un conjunto de vectores del plano a dos vectores {{sube|porcentaje=+30%|contenido=<math>\vec{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\vec{y}</math>}}, con distintas direcciones (linealmente independientes). La representaremos por {{sube|porcentaje=+10%|contenido=<math>B(\vec{x},\vec{y})</math>}}. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 69: | Línea 84: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Base de vectores del plano | ||
| + | |duracion=9´49" | ||
| + | |url1=https://youtu.be/xRZw8wBYVF0?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Concepto de base de vectores del plano. Ejemplos. | ||
| + | }} | ||
| + | |||
| ===Base ortogonal y ortonormal=== | ===Base ortogonal y ortonormal=== | ||
| {{Caja_Amarilla|texto=Si los dos vectores de una base del plano son perpendiculares entre sí, se dice que forman una '''base ortogonal'''. Si además ambos tienen módulo 1, se dice que forman una '''base ortonormal'''. | {{Caja_Amarilla|texto=Si los dos vectores de una base del plano son perpendiculares entre sí, se dice que forman una '''base ortogonal'''. Si además ambos tienen módulo 1, se dice que forman una '''base ortonormal'''. | ||
| Línea 74: | Línea 96: | ||
| {{p}} | {{p}} | ||
| ===Base canónica de los vectores del plano=== | ===Base canónica de los vectores del plano=== | ||
| - | {{Caja_Amarilla|texto=La '''base canónica''' o '''base usual''' de los vectores del plano, que es una base ortonormal qu representaremos por <math>B(\vec{i}, \vec{j})</math> y cuyos vectores se caracterizan por fijarse a un punto de aplicación común, que es el punto de origen del sistema de referencia o punto cero y que tienen por direcciones la de los ejes de coordenadas, y sentido el de los semiejes positivos.}} | + | {{Caja_Amarilla|texto=La '''base canónica''' o '''base usual''' de los vectores del plano, es una base ortonormal que representaremos por <math>B(\vec{i}, \vec{j})</math>, cuyos vectores se caracterizan por: |
| + | :1) Estan fijados a un punto común, el origen del sistema de referencia o punto (0,0). | ||
| + | :2) Tienen por direcciones la de los ejes de coordenadas. | ||
| + | :3) Tienen el mismo sentido que el de los semiejes positivos.}} | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 93: | Línea 118: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Coordenadas de un vector respecto de una base|enunciado= | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=10´49" | ||
| + | |url1=https://youtu.be/kHmQtBno6cc | ||
| + | |sinopsis=Coordenadas de un vector respecto de una base: Un ejemplo gráfico y otro numérico. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=4´58" | ||
| + | |url1=https://youtu.be/pw7EwZ79KE0 | ||
| + | |sinopsis=Calcula las coordenadas del vector (7,4) respecto de la base B={(-2,-1);(1,1)} | ||
| + | }} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=5´35" | ||
| + | |url1=https://youtu.be/XJBXM55t2YI?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Expresa el vector (5,-3) como combinación lineal de los vectores (-1,2) y (3,1). | ||
| + | }} | ||
| + | }} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás poner un vector como combinación lineal de los vectores de una base y obtener sus coordenadas respecto de ella. | |descripcion=En esta escena podrás poner un vector como combinación lineal de los vectores de una base y obtener sus coordenadas respecto de ella. | ||
| Línea 186: | Línea 232: | ||
| *Multiplicación de un vector por un escalar. | *Multiplicación de un vector por un escalar. | ||
| *Ejemplos y ejercicios. | *Ejemplos y ejercicios. | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Suma y resta de vectores | ||
| + | |duracion=11'23" | ||
| + | |sinopsis=Suma y resta de vectores | ||
| + | |url1=https://youtu.be/OkiIB2fU_JM?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 226: | Línea 278: | ||
| *Propiedades | *Propiedades | ||
| *Vectores colineales | *Vectores colineales | ||
| + | }} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Producto de un escalar por un vector | ||
| + | |duracion=9´46" | ||
| + | |url1=https://youtu.be/Yxy8Yo6Z2Ws?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Producto de un escalar por un vector. Ejemplos. | ||
| + | }} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Suma de vectores | ||
| + | |duracion=7´39" | ||
| + | |url1=https://youtu.be/5eTJKpnP93I?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Suma de vectores. Ejemplos. | ||
| + | }} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Combinación lineal de vectores | ||
| + | |duracion=7´38" | ||
| + | |url1=https://youtu.be/5I9C2hEnhl4?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Combinación lineal de vectores. Ejemplos. | ||
| }} | }} | ||
| ---- | ---- | ||
| Línea 273: | Línea 343: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| + | |||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 174)
Introducción
Veamos unos vídeos introductorios para poder comprender mejor el concepto de base.
Dependencia e independencia lineal de vectores. Ejemplos. Combinación lineal de vectores linealmente independientes.
Dependencia e independencia lineal de vectores. En el plano más de dos vectores son siempre linealmente dependientes.
Base de vectores en el plano
Proposición
- Dados dos vectores
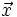 e
e 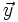 , con distintas direcciones (linealmente independientes), cualquier vector del plano,
, con distintas direcciones (linealmente independientes), cualquier vector del plano, 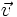 , se puede poner como combinación lineal de ellos:
, se puede poner como combinación lineal de ellos:
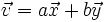
- Esta combinación lineal es única, es decir, sólo existen dos números
 y
y  para los que se cumple la igualdad anterior.
para los que se cumple la igualdad anterior.
1ª parte (Existencia):
Para la demostración de la primera parte tienes el siguiente videotutorial:
Veremos en este video una comprobación geométrica y otra analítica del siguiente resultado:
Dados dos vectores 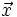 e
e 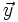 , con distintas direcciones, cualquier vector del plano,
, con distintas direcciones, cualquier vector del plano, 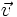 , se puede poner como combinación lineal de ellos:
, se puede poner como combinación lineal de ellos:
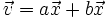
Nota: En el video hace uso de la regla de Cramer, que se ve en el próximo curso, para resolver un sistema 2x2. También lo puedes resolver, usando en su lugar, el método de sustitución.
2ª parte (Unicidad):
Para la demostración de la segunda parte razonaremos por reducción al absurdo. Supondremos que existen dos combinaciones lineales distintas y llegaremos a una contradicción con la hipótesis de partida.
Supongamos que existe dos combinaciones lineales distintas:
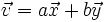
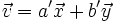
con 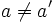 y
y 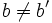
Igualando ambas expresiones:
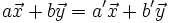
de donde:
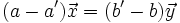
Y como 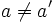 , podemos pasar dividiendo (a-a') que es distinto de cero:
, podemos pasar dividiendo (a-a') que es distinto de cero:
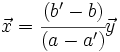
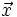 e
e 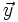 son proporcionales y que, por tanto, tienen la misma dirección. Esto contradice la hipótesis de partida.
son proporcionales y que, por tanto, tienen la misma dirección. Esto contradice la hipótesis de partida.Estos resultados permiten dar la siguiente definición:
Se llama base de un conjunto de vectores del plano a dos vectores 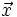 e
e 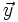 , con distintas direcciones (linealmente independientes). La representaremos por
, con distintas direcciones (linealmente independientes). La representaremos por 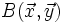 .
.
De esta manera, la proposición anterior se pueden expresar de la siguiente manera:
Teorema de la base
Cualquier vector del plano se puede poner como combinación lineal de los vectores de una base, de forma única.
Concepto de base de vectores del plano. Ejemplos.
Base ortogonal y ortonormal
Si los dos vectores de una base del plano son perpendiculares entre sí, se dice que forman una base ortogonal. Si además ambos tienen módulo 1, se dice que forman una base ortonormal.
Base canónica de los vectores del plano
La base canónica o base usual de los vectores del plano, es una base ortonormal que representaremos por 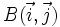 , cuyos vectores se caracterizan por:
, cuyos vectores se caracterizan por:
- 1) Estan fijados a un punto común, el origen del sistema de referencia o punto (0,0).
- 2) Tienen por direcciones la de los ejes de coordenadas.
- 3) Tienen el mismo sentido que el de los semiejes positivos.
Base canónica de vectores del plano.
Nota: En la segunda parte del video se trata el caso de vectores tridimensionales.
Coordenadas de un vector respecto de una base
Dada una base del plano 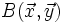 , por el teorema de la base, sabemos que cualquier vector
, por el teorema de la base, sabemos que cualquier vector 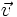 se puede poner como combinación lineal de los vectores de dicha base, de forma única:
se puede poner como combinación lineal de los vectores de dicha base, de forma única:
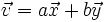
- Al par de números
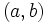 los llamaremos las coordenadas del vector
los llamaremos las coordenadas del vector 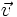 respecto de la base
respecto de la base 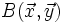 . Lo expresaremos
. Lo expresaremos 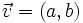 , o bien,
, o bien, 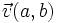 .
.
- Las coordenadas de los vectores de la base son
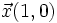 e
e 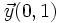 , ya que
, ya que 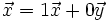 y
y 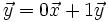 .
.
Coordenadas de un vector respecto de una base: Un ejemplo gráfico y otro numérico.
Calcula las coordenadas del vector (7,4) respecto de la base B={(-2,-1);(1,1)}
Expresa el vector (5,-3) como combinación lineal de los vectores (-1,2) y (3,1).
En esta escena podrás poner un vector como combinación lineal de los vectores de una base y obtener sus coordenadas respecto de ella.
Ejercicio de autoevaluación en el que podrás poner un vector como combinación lineal de otros dos no alineados y que, por tanto, constituyen una base de vectores del plano. En consecuncia podrás averiguar sus coordenadas respecto de dicha base, que serán los números por los que hay que multiplicar los vectores de la base para obtener el vector dado.
Operaciones con vectores dados por coordenadas
Sean 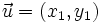 y
y 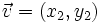 dos vectores del plano:
dos vectores del plano:
- Suma de vectores:
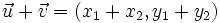
- Producto por un número k:
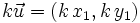
- Combinación lineal:
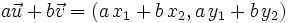
|
Actividad: Operaciones con vectores dados por coordenadas Sean
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) vector 4(-2,1) b) vector (-2,1)-(1,2) c) vector 3(-2,1)+2(1,2) |
(Pág. 175)
Ejercicios resueltos: Operaciones con vectores dados por coordenadas
1. Sean 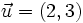 y
y 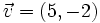 . Halla y comprueba gráficamente que:
. Halla y comprueba gráficamente que:
- a)
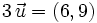
- b)
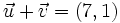
2. Sean 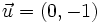 ,
, 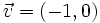 y
y 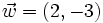 .
.
- Calcula "a" y "b" para que
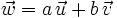 .
.
1a) Utiliza la siguiente escena:
En esta escena podrás ver como se multiplica un vector por un número.
1b) Utiliza la siguiente escena:
En esta escena podrás ver como se suman y restan vectores.
2) Soluciones: a = 3; b = -2
Compruébalo en la siguiente escena:
En esta escena podrás poner un vector como combinación lineal de los vectores de una base y obtener sus coordenadas respecto de ella.
- Suma y resta de vectores.
- Multiplicación de un vector por un escalar.
- Ejemplos y ejercicios.
Suma y resta de vectores
- Sistema de coordenadas rectangulares. Ejemplos.
- Vectores en el plano. Componentes. Ejemplos.
- Suma de vectores y multiplicación de un vector por un escalar. Ejemplos.
Interpretación geométrica de la suma de vectores y multiplicación de un vector por un escalar. Ejemplos.
Combinación lineal de vectores del plano.
Nota: En la segunda parte del video se trata el caso de vectores tridimensionales.
- Suma de vectores: método del paralelogramo.
- Coordenadas del vector suma.
- Propiedades de la suma de vectores.
- Producto de un escalar por un vector
- Propiedades
- Vectores colineales
Producto de un escalar por un vector. Ejemplos.
Suma de vectores. Ejemplos.
Combinación lineal de vectores. Ejemplos.
Encontrar la suma de los vectores dados e ilustrar gráficamente:
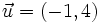 y
y 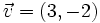
Averigua si los vectores 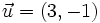 y
y 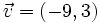 son paralelos o no.
son paralelos o no.
Si 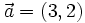 ,
, 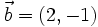 y
y 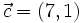 , encuentra
, encuentra 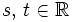 tales que
tales que 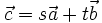 .
.
Sean 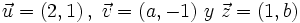 . Halla "a" y "b" en los siguientes casos:
. Halla "a" y "b" en los siguientes casos:
- a)
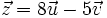
- b)
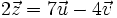
- c)
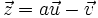
- d)
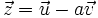
- Demostración de que dados dos vectores
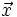 e
e 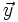 , con distintas direcciones, cualquier vector del plano,
, con distintas direcciones, cualquier vector del plano, 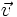 , se puede poner como combinación lineal de ellos.
, se puede poner como combinación lineal de ellos.
- Ejercicio: Si
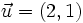 ,
, 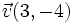 y
y 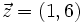 , expresa
, expresa 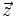 como combinación lineal de los otros dos vectores.
como combinación lineal de los otros dos vectores.
Ejercicios de autoevaluación sobre operaciones con vectores dados por coordenadas.
Ejercicios propuestos
|
Ejercicios propuestos: Coordenadas de un vector |
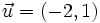 y
y 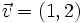 . Representa y halla las coordenadas de los siguientes vectores:
. Representa y halla las coordenadas de los siguientes vectores: