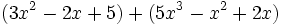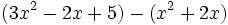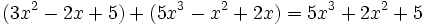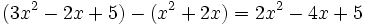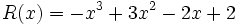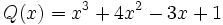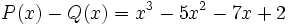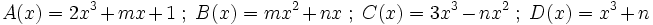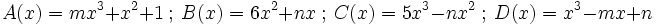Plantilla:Suma y resta de polinomios

De Wikipedia

(Diferencia entre revisiones)
Revisión de 08:18 5 nov 2017
Coordinador (Discusión | contribuciones)

← Ir a diferencia anterior		 Revisión actual
Coordinador (Discusión | contribuciones)

Línea 16: Línea 16:
{{Video_enlace_tutomate {{Video_enlace_tutomate
|titulo1=Tutorial 1 |titulo1=Tutorial 1
-|duracion=4'09"+|duracion=7'35"
|sinopsis=Aprende a sumar y restar polinomios |sinopsis=Aprende a sumar y restar polinomios
-|url1=https://www.youtube.com/watch?v=ueJtyB2Hg2I+|url1=https://www.youtube.com/watch?v=1L_zBNWEANk&list=PLWRbPOo5oaTcfeSnw_WhNua0bmjHpwort&index=1
}} }}
{{Video_enlace_clasematicas {{Video_enlace_clasematicas
Línea 28: Línea 28:
{{Video_enlace_paps {{Video_enlace_paps
|titulo1=Tutorial 3a (Suma) |titulo1=Tutorial 3a (Suma)
-|duracion=7'35"+|duracion=4'09"
|sinopsis=Aprende a sumar polinomios |sinopsis=Aprende a sumar polinomios
-|url1=https://www.youtube.com/watch?v=1L_zBNWEANk&list=PLWRbPOo5oaTcfeSnw_WhNua0bmjHpwort&index=1+|url1=https://www.youtube.com/watch?v=ueJtyB2Hg2I
}} }}
{{Video_enlace_paps {{Video_enlace_paps
Línea 72: Línea 72:
|url1=https://www.youtube.com/watch?v=GAdjF2hF_vs&index=4&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z |url1=https://www.youtube.com/watch?v=GAdjF2hF_vs&index=4&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z
 +}}
 +{{Video_enlace_pildoras
 +|titulo1=Tutorial 6
 +|duracion=9'25"
 +|sinopsis=Suma y resta de polinomios.
 +|url1=https://youtu.be/ROhYH07cdoA?list=PLwCiNw1sXMSDgbsuqToHr0F45-YoSUP7d
}} }}
---- ----
Línea 106: Línea 112:
|url1=https://www.youtube.com/watch?v=2KbR_siNsqc |url1=https://www.youtube.com/watch?v=2KbR_siNsqc
}} }}
-{{Video_enlace_fonemato+{{Video_enlace_khan
-|titulo1=Ejercicio 6+|titulo1=Ejercicio 6a
-|duracion=6'49"+|duracion=3'29"
-|sinopsis=2 ejercicios.+|sinopsis=Simplifica: <math>(5x^2+8x-3)+(2x^2-7x+13x)\;</math>
-|url1=https://www.youtube.com/watch?v=STagSTBlj28&list=PL54E0E2B3C3F7EA2B&index=3+|url1=https://youtu.be/BXngPyAAY9M
 +}}
 +{{Video_enlace_khan
 +|titulo1=Ejercicio 6b
 +|duracion=2'17"
 +|sinopsis=Simplifica: <math>(16x+14)-(3x^2+x-9)\;</math>
 +|url1=https://youtu.be/hU5aasVpI8o
 +}}
 +{{Video_enlace_khan
 +|titulo1=Ejercicio 6c
 +|duracion=7'38"
 +|sinopsis=Resta <math>-2x^2+4x-1\;</math> de <math>6x^2+3x-9\;</math>.
 +|url1=https://youtu.be/fcqZ-M60478
 +}}
 +{{Video_enlace_khan
 +|titulo1=Ejercicio 6d
 +|duracion=3'57"
 +|sinopsis=Simplifica: <math>(x^3+3x-6)+(-2x^2+x-2)-(3x-4)\;</math>
 +|url1=https://youtu.be/ZMmqkr_WitA
 +}}
 +{{Video_enlace_khan
 +|titulo1=Ejercicio 6e
 +|duracion=3'07"
 +|sinopsis=Simplifica: <math>(4x^2y-3x^2-2y)+(8xy-3x^2+2x^2y+4)\;</math>
 +|url1=https://youtu.be/y0Oy_3KEiiY
 +}}
 +{{Video_enlace_khan
 +|titulo1=Ejercicio 6f
 +|duracion=2'47"
 +|sinopsis=Simplifica: <math>(4x^2y-3xy+25)-(9y^2x+7xy-20)\;</math>
 +|url1=https://youtu.be/dU06gyo_0Dk
 +}}
 +{{Video_enlace_khan
 +|titulo1=Ejercicio 6g
 +|duracion=4'14"
 +|sinopsis=Resta <math>-6x^4-3x^2y^2+5y^4\;</math> de <math>2x^4-8x^2y^2-y^4\;</math>.
 +|url1=https://youtu.be/eXFnHQ5Zm20
 +}}
 +{{Video_enlace_khan
 +|titulo1=Ejercicio 6h
 +|duracion=2'52"
 +|sinopsis=Encuentra el error cometido en la resta que se muestra en el video.
 +|url1=https://youtu.be/GDQCuxhGaUU
}} }}
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 7+|titulo1=Ejercicio 7a
|duracion=13'40" |duracion=13'40"
|sinopsis= |sinopsis=
1) Ordena los polinomios y realiza las sumas que se indican: 1) Ordena los polinomios y realiza las sumas que se indican:
-:<math>P(x)=2x^2-3x^3+2x^4+3x^5\;</math>+:<math>P(x)=2x^2-3x^3+2x^4+3x^5\;</math> ; {{b4}} <math>Q(x)=5x^2-2x+6x^4\;</math>
- +
-:<math>Q(x)=5x^2-2x+6x^4\;</math>+
- +
-:<math>R(x)=2x^2-3x^3+2x^4+3x^5\;</math>+
-:<math>S(x)=-3x^2+4x^3-3x^4-2x^5\;</math>+:<math>R(x)=2x^2-3x^3+2x^4+3x^5\;</math> ; {{b4}} <math>S(x)=-3x^2+4x^3-3x^4-2x^5\;</math>
-1a) P(x)+Q(x)+1a) P(x) + Q(x)
-1b) P(x)+R(x)+1b) P(x) + R(x)
-1c) P(x)+S(x)+1c) P(x) + S(x)
|url1=https://www.youtube.com/watch?v=7famqf0iloE&index=5&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z |url1=https://www.youtube.com/watch?v=7famqf0iloE&index=5&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z
}} }}
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 8+|titulo1=Ejercicio 7b
|duracion=10'49" |duracion=10'49"
|sinopsis=Dados los siguientes polinomios, realiza las sumas que se indican: |sinopsis=Dados los siguientes polinomios, realiza las sumas que se indican:
-:<math>P(x)=2x^2-3x^3+2x^4+3x^5\;</math>+:<math>P(x)=2x^2-3x^3+2x^4+3x^5\;</math> ; {{b4}} <math>Q(x)=5x^2-2x+6x^4\;</math>
-:<math>Q(x)=5x^2-2x+6x^4\;</math>+:<math>R(x)=2x^2-3x^3+2x^4+3x^5\;</math> ; {{b4}} <math>S(x)=-3x^2+4x^3-3x^4-2x^5\;</math>
-:<math>R(x)=2x^2-3x^3+2x^4+3x^5\;</math>+1d) Q(x) + S(x)
-:<math>S(x)=-3x^2+4x^3-3x^4-2x^5\;</math>+1e) R(x) + S(x)
- +
-1d) Q(x)+S(x)+
- +
-1e) R(x)+S(x)+
- +
-1f) Q(x)+R(x)+
 +1f) Q(x) + R(x)
|url1=https://www.youtube.com/watch?v=QA9QbWLP25I&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=6 |url1=https://www.youtube.com/watch?v=QA9QbWLP25I&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=6
}} }}
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 9+|titulo1=Ejercicio 8a
|duracion=17'35" |duracion=17'35"
-|sinopsis=Ejercicios 2-3c: Sumar polinomios. Polinomios opuestos+|sinopsis=2) Sumas los siguientes polinomios y compara el grado del polinomio suma con el grado de los polinomios sumandos.
 + 
 +:<math>R(x)=-x^3+3x^2-2x+2\;</math>
 + 
 +:<math>Q(x)=x^3+4x^2-3x+1\;</math>
 + 
 +3a) Escribe opuestos de los siguientes polinomios:
 + 
 +:<math>P(x)=-2x^4-3x^2+2\;</math> ; {{b4}} <math>Q(x)=x^3-4x+1\;</math>
 + 
 +:<math>R(x)=2x^4-3x^3-4x^2+3\;</math> ; {{b4}} <math>S(x)=-x^3+5x+4\;</math>
 + 
 +:<math>T(x)=x^2-x+1\;</math> ; {{b4}} <math>M(x)=-2x^2+4x-2\;</math>
 + 
 +3b) Suma cada uno de los polinomios del apartado anterior con su opuesto.
 + 
 +3c) Calcula un polinomio A(x) tal que <math>P(x)+A(x)=x^2-1\;</math>, siendo <math>P(x)=-2x^4-3x^2+2\;</math>.
|url1=https://www.youtube.com/watch?v=lu2s5qKQKAI&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=7 |url1=https://www.youtube.com/watch?v=lu2s5qKQKAI&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=7
}} }}
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 10+|titulo1=Ejercicio 8b
|duracion=16'45" |duracion=16'45"
-|sinopsis=Ejercicios 3d-f: Aplicar equivalencias fundamentales a polinomios.+|sinopsis=Dados los siguientes polinomios:
 + 
 +:<math>P(x)=-2x^4-3x^2+2\;</math> ; {{b4}} <math>Q(x)=x^3-4x+1\;</math>
 + 
 +:<math>R(x)=2x^4-3x^3-4x^2+3\;</math> ; {{b4}} <math>S(x)=-x^3+5x+4\;</math>
 + 
 +3d) Calcula un polinomio B(x) tal que <math>Q(x)-B(x)=3x^3-x+2\;</math>.
 + 
 +3e) Calcula un polinomio C(x) tal que <math>P(x)+Q(x)-C(x)=R(x)\;</math>.
 + 
 +3f) Calcula un polinomio D(x) tal que <math>R(x)+S(x)-D(x)=0\;</math>.
|url1=https://www.youtube.com/watch?v=n56tBwVdbeg&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=8 |url1=https://www.youtube.com/watch?v=n56tBwVdbeg&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=8
}} }}
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 11+|titulo1=Ejercicio 9
|duracion=12'30" |duracion=12'30"
-|sinopsis=Ejercicio 4: Sumar y restar polinomios.+|sinopsis=Dados los polinomios:
 + 
 +:<math>P(x)=-2x^4-3x^2+2\;</math> ; {{b4}} <math>Q(x)=x^3-4x+1\;</math>
 + 
 +:<math>R(x)=2x^4-3x^3-4x^2+3\;</math> ; {{b4}} <math>S(x)=-x^3+5x+4\;</math>
 + 
 +:<math>T(x)=x^2-x+1\;</math> ; {{b4}} <math>M(x)=-2x^2+4x-2\;</math>
 + 
 +4a) Calcula P(x) - Q(x).
 + 
 +4b) Calcula P(x) - R(x).
 + 
 +4c) Calcula [P(x) + Q(x)]-[R(x) + S(x)]
 + 
 +4d) Calcula [P(x) + S(x)]-[Q(x) + R(x)]
 + 
 +4e) Calcula T(x) + M(x)
 + 
 +4f) Calcula T(x) - M(x)
|url1=https://www.youtube.com/watch?v=mrckQrOh_Zw&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=9 |url1=https://www.youtube.com/watch?v=mrckQrOh_Zw&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=9
}} }}
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 12+|titulo1=Ejercicio 10
|duracion=16'53" |duracion=16'53"
-|sinopsis=Ejercicios 5-8: Cálculos con polinomios. +|sinopsis=5) ¿Qué polinomio se ha de restar al polinomio <math>P(x)=2x^2-4x+2\;</math> para obtener el polinomio <math>x^3-3x+1\;</math>?
 + 
 +6) Dados los polinomios
 + 
 +:<math>P(x)=mx^3-5x+6\;</math> ; {{b4}} <math>Q(x)=-4x^3-6x+7\;</math>
 + 
 +calcula el valor de <math>m\;</math> sabiendo que <math>P(x)+Q(x)=x^3-11x+13\;</math>.
 + 
 +7) Escribe dos polinomios de tercer grado de tal modo que su suma se el polinomio nulo.
 + 
 +8) Escribe dos polinomios reducidos de segundo grado y comprueba con ellos la conmutatividad de la suma.
|url1=https://www.youtube.com/watch?v=IOXPUUt2dSs&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=10 |url1=https://www.youtube.com/watch?v=IOXPUUt2dSs&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=10
}} }}
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 13+|titulo1=Ejercicio 11
|duracion=14'20" |duracion=14'20"
-|sinopsis=Ejercicios 9-11: Valor numérico y problemas con polinomios. +|sinopsis=9) Dado el polinomio <math>P(x)=2x^2-3x+2\;</math>, escribe su opuesto, -P(x). Calcula los valores numéricos de P(x) y -P(x) para x = 0, x = 1 y x = 2, y comprueba comprueba que son números opuestos.
 + 
 +10) ¿Qué polinomio tienes que sumar con <math>3x^2-2x-3\;</math> para que la suma sea 5x^3-6x?
 + 
 +11) Dado el polinomio <math>P(x)=\cfrac{5}{4}x^4-2x^3+6x-\cfrac{1}{5}\;</math>, halla otro polinomio Q(x) tal que <math>P(x)+Q(x)=3x^2+6x-1\;</math>.
|url1=https://www.youtube.com/watch?v=RI3p2CzkFTo&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=11 |url1=https://www.youtube.com/watch?v=RI3p2CzkFTo&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=11
}} }}
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 14+|titulo1=Ejercicio 12
|duracion=7'27" |duracion=7'27"
-|sinopsis=Ejercicio 12: Calcular sumas y restas de polinomios.+|sinopsis=Dados los polinomios
 + 
 +:<math>P(x)=3x^2-1\;</math> ; {{b4}} <math>Q(x)=2x^3-2x^2+4x-2\;</math>
 + 
 +:<math>R(x)=3x^2+x+3\;</math> ; {{b4}} <math>S(x)=\cfrac{1}{2}x^2+2\;</math>
 + 
 +:<math>T(x)=\cfrac{3}{2}x^2+3\;</math> ; {{b4}} <math>V(x)=3x^2+1\;</math>
 + 
 +12a) Calcula P(x) + Q(x).
 + 
 +12b) Calcula P(x) - V(x).
 + 
 +12c) Calcula P(x) + R(x).
 + 
 +12d) Calcula P(x) - R(x).
 + 
 +12e) Calcula S(x) + T(x) + V(x).
 + 
 +12f) Calcula S(x) - T(x) + V(x).
|url1=https://www.youtube.com/watch?v=wduetGOYCl8&index=12&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z |url1=https://www.youtube.com/watch?v=wduetGOYCl8&index=12&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z
}} }}
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 15+|titulo1=Ejercicio 13
|duracion=11'55" |duracion=11'55"
-|sinopsis=Ejercicios 13-16: Contestar preguntas sobre polinomios.+|sinopsis=13) Dados los polinomios
-|url1=https://www.youtube.com/watch?v=dU8lw09JouM&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=13+:<math>P(x)=-x^3+2x^2+x\;</math> ; {{b4}} <math>Q(x)=2x^3-3x+1\;</math>
-}}+ 
 +calcula el polinomio M(x) tal que P(x) + M(x) = Q(x).
{{Video_enlace_escuela {{Video_enlace_escuela
-|titulo1=Ejercicio 16+|titulo1=Ejercicio 14
|duracion=15'13" |duracion=15'13"
-|sinopsis=Ejercicios 17-19: Sumar y restar polinomios. Aplicar equivalencias fundamentales. +|sinopsis=17) La diferencia de dos polinomios es:
 + 
 +:<math>P(x)-Q(x)=x^3-5x^2-7x+2\;</math>
 + 
 +Calcula <math>Q(x)\;</math> sabiendo que <math>P(x)=x^4+5x^3+2x-1\;</math>.
 + 
 +18) ¿Qué polinomio hay que sumar al polinomio <math>P(x)=x^2-6x+3\;</math> para obtener el polinomio opuesto de <math>Q(x)=-5x^3+2x^2-4x+1\;</math>?
 + 
 +19) Dados los polinomios:
 + 
 +:<math>P(x)=x^4-3x^2+2x-3\;</math>; {{b4}} <math>Q(x)=3x^3-4x^2+4\;</math>; {{b4}} <math>R(x)=2x^4-4x-1\;</math>
 + 
 +:19a) Calcula P(x) + Q(x) - R(x)
 + 
 +:19b) Calcula P(x) + R(x) - Q(x)
 + 
 +:19c) Calcula Q(x) + R(x) - P(x)
 + 
 +:19d) Calcula P(x) + Q(x) + R(x)
|url1=https://www.youtube.com/watch?v=CWQypO7oKqo&index=14&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z |url1=https://www.youtube.com/watch?v=CWQypO7oKqo&index=14&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z
}} }}
 +14) Escribe dos polinomios cualesquiera y súmalos. Contesta:
 +
 +:14a) ¿Es mayor el grado de los sumandos o el de la suma? ¿Es igual? ¿Es menor?
 +
 +:14b) ¿Puede en algún caso ser menor el grado de la suma que el de los sumandos? ¿Cuándo? Justifícalo con ejemplos.
 +
 +15) ¿Qué puedes decir del grado de la diferencia de dos polinomios?
 +
 +16) escribe dos polinomios de tercer grado de modo que su suma se el polinomio <math>P(x)=3x^2-5x+3\;</math>.
 +
 +|url1=https://www.youtube.com/watch?v=dU8lw09JouM&list=PLw7Z_p6_h3oz2ZwbEq1hT9DGndGgcOi2z&index=13
 +}}
 +{{Video_enlace_fonemato
 +|titulo1=Ejercicio 15
 +|duracion=6'49"
 +|sinopsis=Determina el valor de "m" y "n" sabiendo que <math>A(x)+B(x) = C(x)-D(x)\;</math>, en los siguientes casos:
 +
 +# <math>A(x)=2x^3+mx+1 \ ; \ B(x)=mx^2+nx \ ; \ C(x)=3x^3-nx^2 \ ; \ D(x)=x^3+n</math>
 +# <math>A(x)=mx^3+x^2+1 \ ; \ B(x)=6x^2+nx \ ; \ C(x)=5x^3-nx^2 \ ; \ D(x)=x^3-mx+n</math>
 +|url1=https://www.youtube.com/watch?v=STagSTBlj28&list=PL54E0E2B3C3F7EA2B&index=3
 +}}
 +
}} }}
{{p}} {{p}}
 +{{Actividades|titulo=Suma y resta de polinomios|enunciado=
{{AI_cidead {{AI_cidead
-|titulo1=Suma y resta de polinomios+|titulo1=Actividad 1
|descripcion=Actividades para aprender y practicar la suma y resta de polinomios. |descripcion=Actividades para aprender y practicar la suma y resta de polinomios.
Línea 221: Línea 378:
}} }}
{{AI_cidead {{AI_cidead
-|titulo1=Ejercicios: ''Suma y resta de polinomios''+|titulo1=Actividad 2
|descripcion=Ejercicios para practicar la suma y resta de polinomios. |descripcion=Ejercicios para practicar la suma y resta de polinomios.
|url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_contenidos_3b.htm |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_contenidos_3b.htm
 +}}
 +{{AI_Khan
 +|titulo1=Autoevaluación 1a (suma)
 +|descripcion=Suma de polinomios.
 +|url1=http://es.khanacademy.org/math/algebra/introduction-to-polynomial-expressions/adding-and-subtracting-polynomials/e/adding_and_subtracting_polynomials
 +}}
 +{{AI_Khan
 +|titulo1=Autoevaluación 1b (resta)
 +|descripcion=Resta de polinomios.
 +|url1=http://es.khanacademy.org/math/algebra/introduction-to-polynomial-expressions/adding-and-subtracting-polynomials/e/subtract-polynomials
 +}}
 +{{AI_Khan
 +|titulo1=Autoevaluación 1c
 +|descripcion=Suma y resta de polinomios.
 +|url1=http://es.khanacademy.org/math/algebra/introduction-to-polynomial-expressions/adding-and-subtracting-polynomials/e/add---subtract-polynomials-challenge
 +}}
 +{{AI_Khan
 +|titulo1=Autoevaluación 1d
 +|descripcion=Suma y resta de polinomios con dos variables.
 +|url1=http://es.khanacademy.org/math/algebra/introduction-to-polynomial-expressions/add-subtract-poly-two-var/e/adding-and-subtracting-polynomials-2
 +}}
 +{{AI_Khan
 +|titulo1=Autoevaluación 1e
 +|descripcion=Suma y resta de polinomios con dos variables.
 +|url1=http://es.khanacademy.org/math/algebra/introduction-to-polynomial-expressions/add-subtract-poly-two-var/e/add---subtract-polynomials--two-variables-challenge
 +}}
 +{{AI_Khan
 +|titulo1=Autoevaluación 1f
 +|descripcion=Suma y resta de polinomios con dos variables: encuentra el error.
 +|url1=http://es.khanacademy.org/math/algebra/introduction-to-polynomial-expressions/add-subtract-poly-two-var/e/add---subtract-polynomials--find-the-error
 +}}
 +{{AI_upr
 +|titulo1=Autoevaluación 2a (suma)
 +|descripcion=Suma de polinomios.
 +|url1=http://quiz.uprm.edu/cgi-bin/Quiz/oneques.cgi?database=REVIEW/exp_alg_tut/exp_alg_tut3_sp.db&no_ques=3
 +}}
 +{{AI_upr
 +|titulo1=Autoevaluación 2b (resta)
 +|descripcion=Resta de polinomios.
 +|url1=http://quiz.uprm.edu/cgi-bin/Quiz/oneques.cgi?database=REVIEW/exp_alg_tut/exp_alg_tut4_sp.db&no_ques=2
}} }}
{{AI_vitutor {{AI_vitutor
|descripcion=Ejercicios de autoevaluación sobre suma y resta de polinomios. |descripcion=Ejercicios de autoevaluación sobre suma y resta de polinomios.
|url1=http://www.vitutor.com/ab/p/poli_21_e.html |url1=http://www.vitutor.com/ab/p/poli_21_e.html
-|titulo1=Autoevaluación: ''Suma y resta de polinomios''+|titulo1=Autoevaluación 3
 +}}
}} }}

Revisión actual

ejercicio

Procedimiento

Para sumar o restar polinomios, sumaremos o restaremos los monomios semejantes de ambos.

ejercicio

Ejemplos: Suma y resta de polinomios

Calcula:

a) (3x^2 - 2x + 5 ) + ( 5x^3 - x^2 + 2x ) \;\!
b) (3x^2 - 2x + 5 ) - ( x^2 + 2x) \;\!
Solución:

a) (3x^2 - 2x + 5 ) + ( 5x^3 - x^2 + 2x ) = 5x^3+2x^2+5 \;\!

b) (3x^2 - 2x + 5 ) - (x^2 + 2x ) = 2x^2-4x+5 \;\!

video
Suma y resta de polinomios
Tutorial 1 (7'35")     Sinopsis:

Aprende a sumar y restar polinomios

Tutorial 2 (23'12")     Sinopsis:

En este tutorial se explica la suma y resta de polinomios comenzando con algunas definiciones básicas y terminando con ejemplos.

Tutorial 3a (Suma) (4'09")     Sinopsis:

Aprende a sumar polinomios

Tutorial 3b (Resta) (4'37")     Sinopsis:

Aprende a restar polinomios

Tutorial 4 (6'57")     Sinopsis:

Suma y resta de polinomios en una variable. Ejemplos.

Tutorial 5a (Suma) (12'33")     Sinopsis:

Suma de polinomios. Ejemplos.

Tutorial 5b (Propiedades de la suma I) (14'39")     Sinopsis:

Propiedades de la suma de polinomios: conmutativa y asociativa.

Tutorial 5c (Propiedades de la suma II) (5'40")     Sinopsis:

Propiedades de la suma de polinomios: Elemento neutro y opuesto.

Tutorial 5d (Resta) (7'58")     Sinopsis:

Resta de polinomios. Equivalencias fundamentales.

Tutorial 6 (9'25")     Sinopsis:

Suma y resta de polinomios.

Ejercicio 1 (2'55")     Sinopsis:

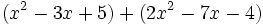
Calcula la suma: (x^2-3x+5)+(2x^2-7x-4)\,

Ejercicio 2 (3'15")     Sinopsis:

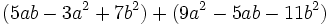
Calcula la suma: (5ab-3a^2+7b^2)+(9a^2-5ab-11b^2)\,

Ejercicio 3 (2'51")     Sinopsis:

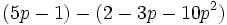
Calcula la resta: (5p-1)-(2-3p-10p^2)\,

Ejercicio 4 (6'27")     Sinopsis:

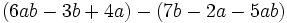
Calcula la resta: (6ab-3b+4a)-(7b-2a-5ab)\,

Ejercicio 5 (8'56")     Sinopsis:

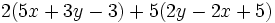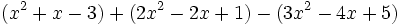
Calcula: a) 2(5x+3y-3)+5(2y-2x+5)\, b) (x^2+x-3)+(2x^2-2x+1)-(3x^2-4x+5)\,

Ejercicio 6a (3'29")     Sinopsis:

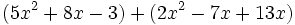
Simplifica: (5x^2+8x-3)+(2x^2-7x+13x)\;

Ejercicio 6b (2'17")     Sinopsis:

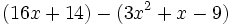
Simplifica: (16x+14)-(3x^2+x-9)\;

Ejercicio 6c (7'38")     Sinopsis:

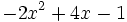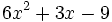Resta -2x^2+4x-1\; de 6x^2+3x-9\;.

Ejercicio 6d (3'57")     Sinopsis:

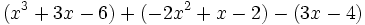
Simplifica: (x^3+3x-6)+(-2x^2+x-2)-(3x-4)\;

Ejercicio 6e (3'07")     Sinopsis:

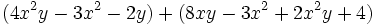
Simplifica: (4x^2y-3x^2-2y)+(8xy-3x^2+2x^2y+4)\;

Ejercicio 6f (2'47")     Sinopsis:

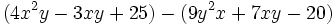
Simplifica: (4x^2y-3xy+25)-(9y^2x+7xy-20)\;

Ejercicio 6g (4'14")     Sinopsis:

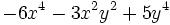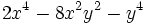Resta -6x^4-3x^2y^2+5y^4\; de 2x^4-8x^2y^2-y^4\;.

Ejercicio 6h (2'52")     Sinopsis:

Encuentra el error cometido en la resta que se muestra en el video.

Ejercicio 7a (13'40")     Sinopsis:

1) Ordena los polinomios y realiza las sumas que se indican:

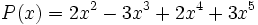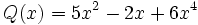
P(x)=2x^2-3x^3+2x^4+3x^5\; ;      Q(x)=5x^2-2x+6x^4\;
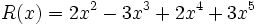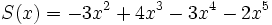
R(x)=2x^2-3x^3+2x^4+3x^5\; ;      S(x)=-3x^2+4x^3-3x^4-2x^5\;

1a) P(x) + Q(x)

1b) P(x) + R(x)

1c) P(x) + S(x)

Ejercicio 7b (10'49")     Sinopsis:

Dados los siguientes polinomios, realiza las sumas que se indican:

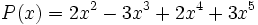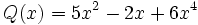
P(x)=2x^2-3x^3+2x^4+3x^5\; ;      Q(x)=5x^2-2x+6x^4\;
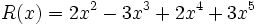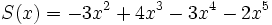
R(x)=2x^2-3x^3+2x^4+3x^5\; ;      S(x)=-3x^2+4x^3-3x^4-2x^5\;

1d) Q(x) + S(x)

1e) R(x) + S(x)

1f) Q(x) + R(x)

Ejercicio 8a (17'35")     Sinopsis:

2) Sumas los siguientes polinomios y compara el grado del polinomio suma con el grado de los polinomios sumandos.

R(x)=-x^3+3x^2-2x+2\;
Q(x)=x^3+4x^2-3x+1\;

3a) Escribe opuestos de los siguientes polinomios:

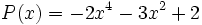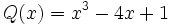
P(x)=-2x^4-3x^2+2\; ;      Q(x)=x^3-4x+1\;
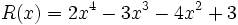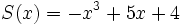
R(x)=2x^4-3x^3-4x^2+3\; ;      S(x)=-x^3+5x+4\;
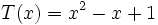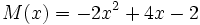
T(x)=x^2-x+1\; ;      M(x)=-2x^2+4x-2\;

3b) Suma cada uno de los polinomios del apartado anterior con su opuesto.

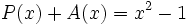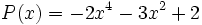3c) Calcula un polinomio A(x) tal que P(x)+A(x)=x^2-1\;, siendo P(x)=-2x^4-3x^2+2\;.

Ejercicio 8b (16'45")     Sinopsis:

Dados los siguientes polinomios:

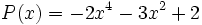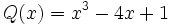
P(x)=-2x^4-3x^2+2\; ;      Q(x)=x^3-4x+1\;
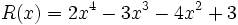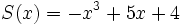
R(x)=2x^4-3x^3-4x^2+3\; ;      S(x)=-x^3+5x+4\;

3d) Calcula un polinomio B(x) tal que 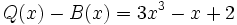Q(x)-B(x)=3x^3-x+2\;.

3e) Calcula un polinomio C(x) tal que 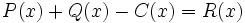P(x)+Q(x)-C(x)=R(x)\;.

3f) Calcula un polinomio D(x) tal que 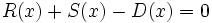R(x)+S(x)-D(x)=0\;.

Ejercicio 9 (12'30")     Sinopsis:

Dados los polinomios:

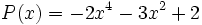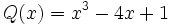
P(x)=-2x^4-3x^2+2\; ;      Q(x)=x^3-4x+1\;
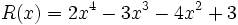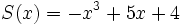
R(x)=2x^4-3x^3-4x^2+3\; ;      S(x)=-x^3+5x+4\;
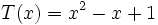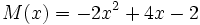
T(x)=x^2-x+1\; ;      M(x)=-2x^2+4x-2\;

4a) Calcula P(x) - Q(x).

4b) Calcula P(x) - R(x).

4c) Calcula [P(x) + Q(x)]-[R(x) + S(x)]

4d) Calcula [P(x) + S(x)]-[Q(x) + R(x)]

4e) Calcula T(x) + M(x)

4f) Calcula T(x) - M(x)

Ejercicio 10 (16'53")     Sinopsis:

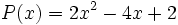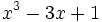5) ¿Qué polinomio se ha de restar al polinomio P(x)=2x^2-4x+2\; para obtener el polinomio x^3-3x+1\;?

6) Dados los polinomios

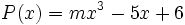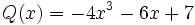
P(x)=mx^3-5x+6\; ;      Q(x)=-4x^3-6x+7\;

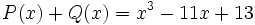calcula el valor de m\; sabiendo que P(x)+Q(x)=x^3-11x+13\;.

7) Escribe dos polinomios de tercer grado de tal modo que su suma se el polinomio nulo.

8) Escribe dos polinomios reducidos de segundo grado y comprueba con ellos la conmutatividad de la suma.

Ejercicio 11 (14'20")     Sinopsis:

9) Dado el polinomio 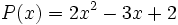P(x)=2x^2-3x+2\;, escribe su opuesto, -P(x). Calcula los valores numéricos de P(x) y -P(x) para x = 0, x = 1 y x = 2, y comprueba comprueba que son números opuestos.

10) ¿Qué polinomio tienes que sumar con 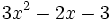3x^2-2x-3\; para que la suma sea 5x^3-6x?

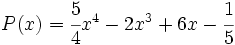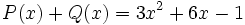11) Dado el polinomio P(x)=\cfrac{5}{4}x^4-2x^3+6x-\cfrac{1}{5}\;, halla otro polinomio Q(x) tal que P(x)+Q(x)=3x^2+6x-1\;.

Ejercicio 12 (7'27")     Sinopsis:

Dados los polinomios

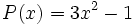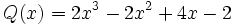
P(x)=3x^2-1\; ;      Q(x)=2x^3-2x^2+4x-2\;
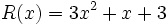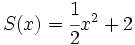
R(x)=3x^2+x+3\; ;      S(x)=\cfrac{1}{2}x^2+2\;
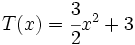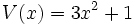
T(x)=\cfrac{3}{2}x^2+3\; ;      V(x)=3x^2+1\;

12a) Calcula P(x) + Q(x).

12b) Calcula P(x) - V(x).

12c) Calcula P(x) + R(x).

12d) Calcula P(x) - R(x).

12e) Calcula S(x) + T(x) + V(x).

12f) Calcula S(x) - T(x) + V(x).

Ejercicio 13 (11'55")     Sinopsis:

13) Dados los polinomios

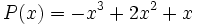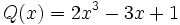
P(x)=-x^3+2x^2+x\; ;      Q(x)=2x^3-3x+1\;

calcula el polinomio M(x) tal que P(x) + M(x) = Q(x).

Ejercicio 14 (15'13")     Sinopsis:

17) La diferencia de dos polinomios es:

P(x)-Q(x)=x^3-5x^2-7x+2\;

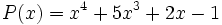Calcula Q(x)\; sabiendo que P(x)=x^4+5x^3+2x-1\;.

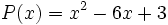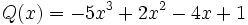18) ¿Qué polinomio hay que sumar al polinomio P(x)=x^2-6x+3\; para obtener el polinomio opuesto de Q(x)=-5x^3+2x^2-4x+1\;?

19) Dados los polinomios:

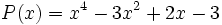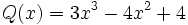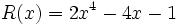
P(x)=x^4-3x^2+2x-3\;;      Q(x)=3x^3-4x^2+4\;;      R(x)=2x^4-4x-1\;
19a) Calcula P(x) + Q(x) - R(x)
19b) Calcula P(x) + R(x) - Q(x)
19c) Calcula Q(x) + R(x) - P(x)
19d) Calcula P(x) + Q(x) + R(x)

14) Escribe dos polinomios cualesquiera y súmalos. Contesta:

14a) ¿Es mayor el grado de los sumandos o el de la suma? ¿Es igual? ¿Es menor?
14b) ¿Puede en algún caso ser menor el grado de la suma que el de los sumandos? ¿Cuándo? Justifícalo con ejemplos.

15) ¿Qué puedes decir del grado de la diferencia de dos polinomios?

16) escribe dos polinomios de tercer grado de modo que su suma se el polinomio 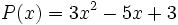P(x)=3x^2-5x+3\;.

Ejercicio 15 (6'49")     Sinopsis:

Determina el valor de "m" y "n" sabiendo que 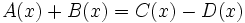A(x)+B(x) = C(x)-D(x)\;, en los siguientes casos:

  1. A(x)=2x^3+mx+1 \ ; \ B(x)=mx^2+nx \ ; \ C(x)=3x^3-nx^2 \ ; \ D(x)=x^3+n
  2. A(x)=mx^3+x^2+1 \ ; \ B(x)=6x^2+nx \ ; \ C(x)=5x^3-nx^2 \ ; \ D(x)=x^3-mx+n

video
Suma y resta de polinomios
Actividad 1     Descripción:

Actividades para aprender y practicar la suma y resta de polinomios.

Actividad 2     Descripción:

Ejercicios para practicar la suma y resta de polinomios.

Autoevaluación 1a (suma)     Descripción:

Suma de polinomios.

Autoevaluación 1b (resta)     Descripción:

Resta de polinomios.

Autoevaluación 1c     Descripción:

Suma y resta de polinomios.

Autoevaluación 1d     Descripción:

Suma y resta de polinomios con dos variables.

Autoevaluación 1e     Descripción:

Suma y resta de polinomios con dos variables.

Autoevaluación 1f     Descripción:

Suma y resta de polinomios con dos variables: encuentra el error.

Autoevaluación 2a (suma)     Descripción:

Suma de polinomios.

Autoevaluación 2b (resta)     Descripción:

Resta de polinomios.

Autoevaluación 3     Descripción:

Ejercicios de autoevaluación sobre suma y resta de polinomios.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Suma_y_resta_de_polinomios"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda