Plantilla:Definición de función (1ººBach)
De Wikipedia
| Revisión de 08:15 12 jun 2017 Coordinador (Discusión | contribuciones) (→Reglas fundamentales) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Concepto de función) |
||
| Línea 7: | Línea 7: | ||
| <center><math> f: A \rightarrow B </math></center> | <center><math> f: A \rightarrow B </math></center> | ||
| {{p}} | {{p}} | ||
| - | *Al conjunto A se le denomina '''conjunto inicial''' y al B '''conjunto final'''.. | + | *Al conjunto A se le denomina '''dominio''' y al B '''codominio'''. |
| + | *A un objeto o valor genérico del dominio A se le denomina '''variable independiente'''; y a un objeto genérico del codominio B, '''variable dependiente'''. | ||
| *Sea <math>x \in A\;</math>, al elemento de B que se corresponda con <math>x\;</math> lo representaremos por <math>f(x)\;</math> y se leerá "''imagen de x según f'' ". (Notación introducida por [[Euler]] en 1734) | *Sea <math>x \in A\;</math>, al elemento de B que se corresponda con <math>x\;</math> lo representaremos por <math>f(x)\;</math> y se leerá "''imagen de x según f'' ". (Notación introducida por [[Euler]] en 1734) | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Se pueden definir funciones entre cualquier tipo de conjuntos, pero las más interesantes son las que se establecen entre conjuntos de números. En este curso estudiaremos funciones definidas en el conjunto de los números reales: las funciones reales (conjunto final) | + | {{Videotutoriales|titulo=Concepto de función|enunciado= |
| - | de variable real (conjunto inicial), <math>f:\mathbb{R} \rightarrow \mathbb{R}</math>. | + | {{Video_enlace_clasematicas |
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=27'16" | ||
| + | |sinopsis=*Concepto de función. | ||
| + | |url1=https://youtu.be/sZIcLmsFknM?list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3 | ||
| + | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=10'47" | ||
| + | |sinopsis=*Concepto de relación o correspondencia. | ||
| + | *Concepto de función. | ||
| + | |url1=https://www.youtube.com/watch?v=Ll7xfe3HoZE | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Tutorial 3 | ||
| + | |duracion=46'32" | ||
| + | |sinopsis=*Definición de función. | ||
| + | *Dominio e imagen (o rango). | ||
| + | *Distintas formas de representar una función. | ||
| + | *Ejercicios resueltos. | ||
| + | |url1=https://www.youtube.com/watch?v=onh9C8dv9x4&list=PL3KGq8pH1bFQCtxruKjQqhM4BTwHARnRR&index=1 | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | Se pueden definir funciones entre cualquier tipo de conjuntos, pero las más interesantes son las que se establecen entre conjuntos de números. En este curso estudiaremos funciones definidas en el conjunto de los números reales: las funciones reales (el conjunto final es un subconjunto de los números reales) de variable real (el conjunto origen es un subconjunto de los números reales). | ||
| {{p}} | {{p}} | ||
| ==Función real de variable real== | ==Función real de variable real== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Una '''función real de variable real''', <math>f\;</math>, es una [[correspondencia]] entre números reales que asocia a cada valor de la '''variable independiente''' <math>x\;</math> un único valor de la '''variable dependiente''' <math>y\;.</math> En tal caso decimos que "<math>y\;</math> '''es función de''' <math>x\;</math>" y lo representamos por <math>y=f(x)\;</math>. | + | Una '''función real de variable real''', <math>f\;</math>, es una [[correspondencia]] entre números reales que asocia a cada elemento <math>x\;</math> de un determinado subconjunto de números reales, <math>Dom\;</math>, llamado '''dominio''', un único número real <math>y\;</math>. En tal caso decimos que "<math>y\;</math> '''es función de''' <math>x\;</math>" y lo representamos por <math>y=f(x)\;</math>. |
| Simbólicamente: | Simbólicamente: | ||
| Línea 23: | Línea 48: | ||
| <center><math> | <center><math> | ||
| \begin{matrix} | \begin{matrix} | ||
| - | f \colon \mathbb{R} & \rightarrow & \mathbb{R} \ \qquad \quad | + | f \colon Dom \subset \mathbb{R} & \rightarrow & \mathbb{R} \ \qquad \quad |
| \\ | \\ | ||
| \quad \ x & \rightarrow & y=f(x) | \quad \ x & \rightarrow & y=f(x) | ||
| \end{matrix} | \end{matrix} | ||
| </math></center> | </math></center> | ||
| + | |||
| + | *A <math>x\;</math> se le llama la '''variable independiente''' y a <math>y\;</math> la '''variable dependiente'''. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 49: | Línea 76: | ||
| {{geogebra: averigua si es funcion}} | {{geogebra: averigua si es funcion}} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Operaciones con funciones== | ==Operaciones con funciones== | ||
| {{Videotutoriales|titulo=Operaciones con funciones|enunciado= | {{Videotutoriales|titulo=Operaciones con funciones|enunciado= | ||
| Línea 70: | Línea 98: | ||
| En el estudio de una función (dominio, límites, continuidad, etc.) hay una serie de "reglas sagradas" que hay que tener muy presentes: | En el estudio de una función (dominio, límites, continuidad, etc.) hay una serie de "reglas sagradas" que hay que tener muy presentes: | ||
| {{p}} | {{p}} | ||
| - | {{Caja_Amarilla|texto= | + | {{Caja_gris|texto= |
| *Prohibido dividir por cero. | *Prohibido dividir por cero. | ||
| *Toda raíz de índice par de un número negativo no es un número real. | *Toda raíz de índice par de un número negativo no es un número real. | ||
| Línea 115: | Línea 143: | ||
| {{p}} | {{p}} | ||
| - | ==Puntos de corte con los ejes== | + | ==Puntos de corte con los ejes de una función== |
| - | {{Caja_Amarilla|texto=Los '''puntos de corte con los ejes''' de coordenadas de una función son los '''ceros''' de la función, es decir, aquellos valores de la variable independiente, x, que hacen f(x)=0.}} | + | {{Definicion: Puntos de corte con los ejes de una función}} |
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Puntos de corte con los ejes|enunciado= | {{Videotutoriales|titulo=Puntos de corte con los ejes|enunciado= | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=3'35" | ||
| + | |url1=https://www.youtube.com/watch?v=FaNynCkCmkc&index=7&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3 | ||
| + | |sinopsis=Tutorial en el que se explica el cálculo de los puntos de corte con los ejes de una función dada su gráfica. | ||
| + | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Los ceros de una función | + | |titulo1=Tutorial 2 |
| |duracion=3'57" | |duracion=3'57" | ||
| |sinopsis=Video tutorial de matematicasbachiller.com | |sinopsis=Video tutorial de matematicasbachiller.com | ||
| Línea 126: | Línea 160: | ||
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Contacto de una curva con los ejes | + | |titulo1=Tutorial 3 |
| |duracion=15'54" | |duracion=15'54" | ||
| |sinopsis=Los puntos en que la gráfica de la función " f " toca al eje de abcisas son las soluciones de la ecuación f(x) = 0. | |sinopsis=Los puntos en que la gráfica de la función " f " toca al eje de abcisas son las soluciones de la ecuación f(x) = 0. | ||
Revisión actual
Tabla de contenidos |
Concepto de función
Sean A y B conjuntos. Se llama función entre A y B a cualquier relación o correspondencia establecida entre los elementos de A y B de tal modo que a cada elemento de A le corresponde un único elemento de B.
- Si llamamos
 a la función entre A y B, ésta podemos expresarla simbólicamente:
a la función entre A y B, ésta podemos expresarla simbólicamente:
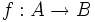
- Al conjunto A se le denomina dominio y al B codominio.
- A un objeto o valor genérico del dominio A se le denomina variable independiente; y a un objeto genérico del codominio B, variable dependiente.
- Sea
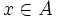 , al elemento de B que se corresponda con
, al elemento de B que se corresponda con  lo representaremos por
lo representaremos por  y se leerá "imagen de x según f ". (Notación introducida por Euler en 1734)
y se leerá "imagen de x según f ". (Notación introducida por Euler en 1734)
- Concepto de función.
- Concepto de relación o correspondencia.
- Concepto de función.
- Definición de función.
- Dominio e imagen (o rango).
- Distintas formas de representar una función.
- Ejercicios resueltos.
Se pueden definir funciones entre cualquier tipo de conjuntos, pero las más interesantes son las que se establecen entre conjuntos de números. En este curso estudiaremos funciones definidas en el conjunto de los números reales: las funciones reales (el conjunto final es un subconjunto de los números reales) de variable real (el conjunto origen es un subconjunto de los números reales).
Función real de variable real
Una función real de variable real,  , es una correspondencia entre números reales que asocia a cada elemento
, es una correspondencia entre números reales que asocia a cada elemento  de un determinado subconjunto de números reales,
de un determinado subconjunto de números reales, 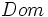 , llamado dominio, un único número real
, llamado dominio, un único número real  . En tal caso decimos que "
. En tal caso decimos que " es función de
es función de  " y lo representamos por
" y lo representamos por  .
.
Simbólicamente:
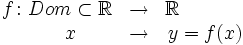
- A
 se le llama la variable independiente y a
se le llama la variable independiente y a  la variable dependiente.
la variable dependiente.
- Definición de función, variable independiente y variable dependiente. Ejemplos
La gráfica de una función real de variable real es una curva plana: cada punto "x" del conjunto inicial junto a su imagen "f(x)" determina un punto (x;f(x)) por el que pasa la gráfica de "f".
En esta escena podrás ver, mediante ejemplos gráficos, como algunas relaciones entre variables son función y otras no.
Operaciones con funciones
Tutorial dedicado a las operaciones básicas con funciones: producto por constante (k·f)(x), suma y resta (f+g)(x), producto y división (f·g)(x).
- Distintas operaciones que se pueden realizar con funciones. Ejemplos.
Reglas fundamentales
En el estudio de una función (dominio, límites, continuidad, etc.) hay una serie de "reglas sagradas" que hay que tener muy presentes:
- Prohibido dividir por cero.
- Toda raíz de índice par de un número negativo no es un número real.
- El logaritmo (en cualquier base) de un número no positivo no es un número real.
Hay ciertas reglas en matemáticas que no se pueden violar. Estas reglas afectan a la hora de determinar el dominio de una función. Aquí las vamos a recordar:
- Prohibido dividir por cero.
- Toda raíz de índice par de un número negativo no es un número real.
- El logaritmo (en cualquier base) de un número no positivo no es un número real.
AVISO: será inmisericordemente suspendido ipso facto todo el que viole una Regla Sagrada; caerán sobre él toneladas de desprestigio y deshonor, y el estigma de tan ignominioso acto apestará la honra de su linaje por los siglos de los siglos.
Hay funciones que a la hora de trabajar con ellas no presentan ningún problema; otras sin embargo son realmente peligrosas.
En relación a los tres conceptos fundamentales del Cálculo (límite, continuidad y derivada de una función "f" en un punto "c"), y debido a las posibles violaciones de las tres Reglas Sagradas, las funciones son como las serpientes: las hay inofensivas y las hay peligrosas. Por eso, al trabajar con una función "f" en el punto "c", lo primero es invertir un par de segundos en analizar si "f" es o no peligrosa en "c". Naturalmente, si es peligrosa, pondremos todos nuestros sentidos en estado de máxima concentración y alerta, para así intentar evitar que nos mande al otro barrio.
En este vídeo vemos ejemplos en los que analizamos la peligrosidad de trabajar (límite, continuidad, derivada) con una cierta función "f" en un cierto punto "c".
Todo se reduce a analizar si en "c" se viola alguna Regla Sagrada; a saber:
- Prohibido dividir por cero.
- Toda raíz de índice par de un número negativo no es un número real.
- El logaritmo (en cualquier base) de un número no positivo no es un número real.
Puntos de corte con los ejes de una función
Los puntos de corte con los ejes de una función son los puntos de la gráfica que pertenecen a los ejes de coordenadas:
- Puntos de corte con el eje de abscisas (eje X): Son aquellos puntos de la función en los que la variable dependiente,
 , toma el valor cero.
, toma el valor cero.
- Punto de corte con el eje de ordenadas (eje Y): Es aquel punto de la función en el que la variable independiente,
 , toma el valor cero.
, toma el valor cero.
Tutorial en el que se explica el cálculo de los puntos de corte con los ejes de una función dada su gráfica.
Video tutorial de matematicasbachiller.com
Los puntos en que la gráfica de la función " f " toca al eje de abcisas son las soluciones de la ecuación f(x) = 0. La gráfica de " f " corta al eje de ordenadas en f(0).
Signo de una función
- Una función decimos que es positiva cuando la variable dependiente toma valores positivos y decimos que es negativa cuando toma valores negativos.
- El estudio del signo de una función consistirá en determinar para qué valores de la variable independiente la función es positiva o negativa.
El estudio del signo de una función va a ser útil en la representación gráfica de funciones y en el estudio del dominio de funciones.
Tutorial en el que se explica el estudio del signo de una función dada su gráfica.
Existe un error en el minuto 5:05 cuando se expresa los valores donde se alcanzan valores positivos, ya que el valor máximo que puede tomar la x es 6 y no infinito
A la hora de representar la gráfica de la función "f", el estudio del signo del número real f(x) nos permite conocer la posición de la gráfica respecto al eje de abcisas.
- La gráfica está por encima del eje de abcisas en los puntos "x" tales que f(x) es positivo.
- La gráfica está por debajo del eje de abcisas en los puntos "x" tales que f(x) es negativo.
- La gráfica toca al eje de abcisas en los puntos "x" tales que f(x) = 0.
El estudio del signo de una función también es útil cuando queremos determinar el dominio de una función.
2 ejercicios sobre el estudio del signo de una función
4 ejercicios sobre el estudio del signo de una función
Dominio e imagen de una función
- Al conjunto de los valores que puede tomar la variable independiente
 , se le llama dominio de definición de la función. Lo representaremos por
, se le llama dominio de definición de la función. Lo representaremos por 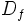 ó
ó 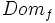
- La imagen, rango o recorrido de una función es el conjunto de valores que puede tomar la variable dependiente
 . Lo representaremos por
. Lo representaremos por 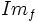 o
o 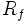 .
.
En esta escena podrás visualizar el dominio y la imagen de una función. Podrás elegir entre un tramo de recta (función lineal) o de parábola (función cuadrática).
Razones para restringir el dominio de una función:
- Imposibilidad de realizar alguna operación con ciertos valores de
 que incumplan las quie hemos llamdo "reglas sagradas" del Cálculo. (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos).
que incumplan las quie hemos llamdo "reglas sagradas" del Cálculo. (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos).
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos).
- Por voluntad de quien propone la función.
Ejemplo: Dominio de definición de una función
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
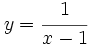
- b)
- c)
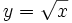
- c)
- d)
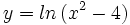
- d)
- e)
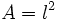 (Área de un cuadrado de lado
(Área de un cuadrado de lado 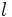 )
)
- e)
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
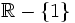 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
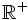 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
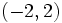 , porque el logaritmo de un número sólo existe si éste es positivo. Al resolver la inecuación
, porque el logaritmo de un número sólo existe si éste es positivo. Al resolver la inecuación 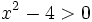 resulta que
resulta que 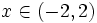 .
.
- d) Su dominio es
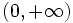 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
El "dominio de definición" de la función "f" se denota Domf, y es el conjunto que forman los números reales "x" que tienen imagen segun "f"; o sea, los "x" tales que al calcular "f(x)" no se viola ninguna Regla Sagrada. A la hora de representar la gráfica de "f" lo primero SIEMPRE es determinar Domf, pues así sabremos en qué puntos del eje de abcisas hay curva y en qué puntos no la hay.
5 ejemplos. Varios ejemplos. 15 ejemplos. 16 ejemplos. 10 ejemplos. 11 ejemplos. | 7 ejemplos. 8 ejemplos. 4 ejemplos. 6 ejemplos. 7 ejemplos. 7 ejemplos. |
Halla el dominio de 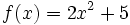 .
.
Halla el dominio de 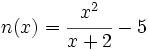 .
.
Halla el dominio de 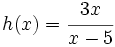 .
.
Halla el dominio de 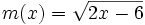 .
.
Halla el dominio de 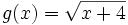 .
.
Halla el dominio de 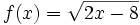 .
.
Halla el dominio de:
- a)
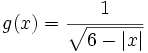 .
.
- b)
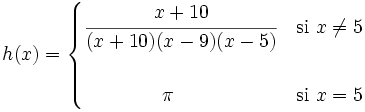
Conceptos de dominio y rango de una función. Ejemplos
Tutorial en el que se explica el cálculo del dominio y la imagen de una función dada su gráfica.
Dominio y rango de una función. Ejemplos.
Dominio e imagen (o rango) de una función. Ejemplos.
Expresa el área de un círculo en función de la longitud de su circunferencia e indica su dominio y recorrido.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones polinómicas.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con quebrados algebraicos.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con radicales.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula y en este caso interviene el valor absoluto de funciones y cuando aparecen mezcladas funciones polinómicas, con quebrados y radicales.
|
Actividad: Dominio e imagen de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Simetrías de una función
- Una función es par si cumple que:
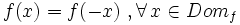 . En tal caso la gráfica es simétrica respecto del eje Y.
. En tal caso la gráfica es simétrica respecto del eje Y.
- Una función es impar si cumple que:
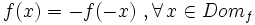 . En tal caso la gráfica es simétrica respecto del origen.
. En tal caso la gráfica es simétrica respecto del origen.
- La función "f" se dice "par" si f(-x) = f(x), y se dice "impar" si f(-x) = -f(x).
- Si "f" es par, su gráfica es simétrica respecto al eje de ordenadas.
- Si "f" es impar, su gráfica es simétrica respecto al origen de coordenadas.
- Obvio: si Dom f. no es simétrico respecto al punto "0", la función "f" no es par ni impar.
Definición de función par e impar. Ejemplos.
Ejemplos de funciones pares e impares. Interpretación gráfica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Ejercicios propuestos
|
Ejercicios propuestos: Concepto de función y de dominio de una función |
 .
.

