Plantilla:Continuidad de una función en un punto

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión de 04:21 18 mar 2020

Una función $f(x)\;$ es continua en un punto $a\;$ , si se cumple que:

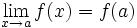
$\lim_{x \to a} f(x)=f(a)$

Para que ésto se cumpla deben ocurrir las tres condiciones siguientes:

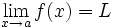
La función $f(x)\;$ tiene límite en $x=a\;$ : Existe $\lim_{x \to a} f(x)=L$
La función está definida en $x=a\;$ : Existe $f(a)\;$
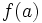
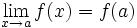
Los dos valores anteriores coinciden: $\lim_{x \to a} f(x)=f(a)$

Continuidad de una función en un punto (13'37") Sinopsis:

La función "f" se dice continua por la izquierda (derecha) en el punto "a" si el límite de "f" en "a" por la izquierda (derecha) es finito y coincide con f(a). Se dice que "f" es continua en "a" si es continua por la izquierda y por la derecha en "a".

Introducción al concepto de continuidad de una función (22'31") Sinopsis:

En este vídeo introduciremos el concepto de continuidad de forma gráfica, calculando los límites laterales a partir de la información de la curva.

Continuidad de una función en un intervalo (4'19") Sinopsis:

Video tutorial de matematicasbachiller.com

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Continuidad_de_una_funci%C3%B3n_en_un_punto"

 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/17-continuidad-de-funciones/02-continuidad-de-una-funcion-en-un-punto-3
+}}
+{{Video_enlace_fonemato
+|titulo1=Introducción al concepto de continuidad de una función
+|duracion=22'31"
+|sinopsis=En este vídeo introduciremos el concepto de continuidad de forma gráfica, calculando los límites laterales a partir de la información de la curva.
+|url1=https://youtu.be/vnvPhRCRxMA
 }}
 {{Video_enlace_fonemato

Plantilla:Continuidad de una función en un punto

De Wikipedia

Revisión de 04:21 18 mar 2020

Vistas

Herramientas personales

Menú

Buscar

Herramientas