Plantilla:Continuidad de una función en un punto
De Wikipedia
| Revisión de 04:34 18 mar 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:22 18 mar 2020 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| *Los dos valores anteriores coinciden: <math>\lim_{x \to a} f(x)=f(a)</math> | *Los dos valores anteriores coinciden: <math>\lim_{x \to a} f(x)=f(a)</math> | ||
| }} | }} | ||
| - | {{p}} | + | {{p}} |
| + | {{Videotutoriales|titulo=Continuidad de una función en un punto|enunciado= | ||
| {{Video_enlace_LaMejorAsesoríaEducativa | {{Video_enlace_LaMejorAsesoríaEducativa | ||
| - | |titulo1=Introducción al concepto de continuidad de una función | + | |titulo1=Tutorial 1 |
| |duracion=22'31" | |duracion=22'31" | ||
| |sinopsis=En este vídeo introduciremos el concepto de continuidad de forma gráfica, calculando los límites laterales a partir de la información de la curva. | |sinopsis=En este vídeo introduciremos el concepto de continuidad de forma gráfica, calculando los límites laterales a partir de la información de la curva. | ||
| |url1=https://youtu.be/vnvPhRCRxMA | |url1=https://youtu.be/vnvPhRCRxMA | ||
| + | }} | ||
| + | {{Video_enlace_TodoSobresaliente | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=31'04" | ||
| + | |sinopsis=En este vídeo definiremos cuando una función es continua en un punto usando el concepto de límite y veremos algunos ejemplos en los que usaremos tablas de valores para calcular los límites laterales. | ||
| + | |url1=https://youtu.be/LDkdAr6m0gg?list=PL8Ee8uJSAwYNNCIxRW0l9SlPOjvYDdKiz | ||
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Continuidad de una función en un punto | + | |titulo1=Tutorial 3 |
| |duracion=13'37" | |duracion=13'37" | ||
| |sinopsis=La función "f" se dice continua por la izquierda (derecha) en el punto "a" si el límite de "f" en "a" por la izquierda (derecha) es finito y coincide con f(a). | |sinopsis=La función "f" se dice continua por la izquierda (derecha) en el punto "a" si el límite de "f" en "a" por la izquierda (derecha) es finito y coincide con f(a). | ||
| Línea 24: | Línea 31: | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/17-continuidad-de-funciones/02-continuidad-de-una-funcion-en-un-punto-3 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/17-continuidad-de-funciones/02-continuidad-de-una-funcion-en-un-punto-3 | ||
| + | }} | ||
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
Revisión de 10:22 18 mar 2020
Una función  es continua en un punto
es continua en un punto  , si se cumple que:
, si se cumple que:
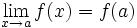
Para que ésto se cumpla deben ocurrir las tres condiciones siguientes:
- La función
 tiene límite en
tiene límite en  : Existe
: Existe 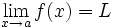
- La función está definida en
 : Existe
: Existe 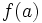
- Los dos valores anteriores coinciden:
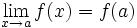
En este vídeo introduciremos el concepto de continuidad de forma gráfica, calculando los límites laterales a partir de la información de la curva.
En este vídeo definiremos cuando una función es continua en un punto usando el concepto de límite y veremos algunos ejemplos en los que usaremos tablas de valores para calcular los límites laterales.
La función "f" se dice continua por la izquierda (derecha) en el punto "a" si el límite de "f" en "a" por la izquierda (derecha) es finito y coincide con f(a). Se dice que "f" es continua en "a" si es continua por la izquierda y por la derecha en "a".
Video tutorial de matematicasbachiller.com

