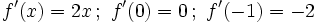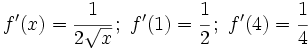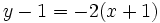Plantilla:Derivada de una función
De Wikipedia
| Revisión de 07:20 28 mar 2020 Coordinador (Discusión | contribuciones) (→Notación) ← Ir a diferencia anterior |
Revisión de 07:35 28 mar 2020 Coordinador (Discusión | contribuciones) (→Notación) Ir a siguiente diferencia → |
||
| Línea 24: | Línea 24: | ||
| }} | }} | ||
| ---- | ---- | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicio 1a | ||
| + | |duracion=7'57" | ||
| + | |sinopsis=Halla la derivada de las siguientes funciones usando la definición de derivada: | ||
| + | |||
| + | # <math>f(x)=3x+5\;</math> | ||
| + | # <math>f(x)=2x-4\;</math> | ||
| + | |||
| + | |url1=https://youtu.be/U7onW7mMzLM | ||
| + | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicio 1b | ||
| + | |duracion=7'56" | ||
| + | |sinopsis=Halla la derivada de las siguientes funciones usando la definición de derivada: | ||
| + | |||
| + | # <math>f(x)=x^2\;</math> | ||
| + | # <math>f(x)=2x^2\;</math> | ||
| + | |||
| + | |url1=https://youtu.be/uLDg8fqsuZg | ||
| + | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicio 1c | ||
| + | |duracion=9'58" | ||
| + | |sinopsis=Halla la derivada de las siguientes funciones usando la definición de derivada: | ||
| + | |||
| + | # <math>f(x)=x^2-4x-5\;</math> | ||
| + | # <math>f(x)=x^2-x+2\;</math> | ||
| + | |||
| + | |url1=https://youtu.be/L0BZlkBbZmI | ||
| + | }} | ||
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejercicio 1 | + | |titulo1=Ejercicio 2 |
| |duracion=9'24" | |duracion=9'24" | ||
| |sinopsis=Halla la derivada de la siguiente función usando la definición de derivada: | |sinopsis=Halla la derivada de la siguiente función usando la definición de derivada: | ||
| Línea 33: | Línea 63: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 2 | + | |titulo1=Ejercicio 3 |
| |duracion=6'44" | |duracion=6'44" | ||
| |sinopsis=Halla la derivada de la siguiente función usando la definición de derivada: | |sinopsis=Halla la derivada de la siguiente función usando la definición de derivada: | ||
| Línea 42: | Línea 72: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 3 | + | |titulo1=Ejercicio 4 |
| |duracion=13'20" | |duracion=13'20" | ||
| |sinopsis=Halla la derivada de la siguiente función usando la definición de derivada: | |sinopsis=Halla la derivada de la siguiente función usando la definición de derivada: | ||
| Línea 51: | Línea 81: | ||
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| - | |titulo1=Ejercicio 4 | + | |titulo1=Ejercicio 5 |
| |duracion=3'24" | |duracion=3'24" | ||
| |sinopsis=Halla la derivada de la siguiente función usando la definición de derivada: | |sinopsis=Halla la derivada de la siguiente función usando la definición de derivada: | ||
| Línea 60: | Línea 90: | ||
| }} | }} | ||
| {{Video_enlace_matesandres | {{Video_enlace_matesandres | ||
| - | |titulo1=Ejercicio 5 | + | |titulo1=Ejercicio 6 |
| |duracion=9'01" | |duracion=9'01" | ||
| |sinopsis=Halla la derivada de las siguientes funciones usando la definición de derivada: | |sinopsis=Halla la derivada de las siguientes funciones usando la definición de derivada: | ||
Revisión de 07:35 28 mar 2020
Se llama función derivada de  , o simplemente derivada de
, o simplemente derivada de  , a una función que llamaremos
, a una función que llamaremos 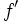 (o bien,
(o bien, 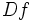 ) que asocia a cada valor
) que asocia a cada valor  , la derivada de
, la derivada de  en ese punto,
en ese punto, 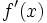 . Es decir,
. Es decir,
|
|
Notación
- Dada una función
 , la función derivada ,
, la función derivada , 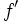 , también se llama la derivada primera de
, también se llama la derivada primera de  . También se suele representar por
. También se suele representar por 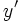 .
.
- La función derivada de
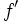 se denomina la derivada segunda de
se denomina la derivada segunda de  y se escribe
y se escribe 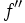 .
.
- Analogamente, tenemos la derivada tercera,
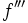 , cuarta
, cuarta 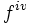 , quinta
, quinta 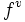 , ...
, ...
¿Qué es la derivada? Derivada de una función en un punto. Función derivada. Simulación en GeoGebra
Otra notación para la función derivada
Halla la derivada de las siguientes funciones usando la definición de derivada:
Halla la derivada de las siguientes funciones usando la definición de derivada:
Halla la derivada de las siguientes funciones usando la definición de derivada:
Halla la derivada de la siguiente función usando la definición de derivada:
Halla la derivada de la siguiente función usando la definición de derivada:
Halla la derivada de la siguiente función usando la definición de derivada:
Halla la derivada de la siguiente función usando la definición de derivada:
Halla la derivada de las siguientes funciones usando la definición de derivada:
El universo de las derivadas
Nota: Requiere Flash Player y ver con Firefox.
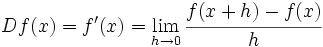
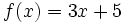
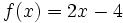

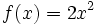
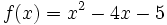
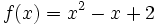
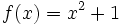
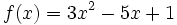
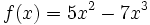
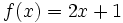
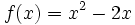
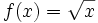
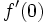 y
y 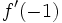 .
.
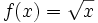 . A partir de ella, calcula
. A partir de ella, calcula 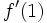 y
y 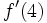 .
.
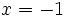 .
.