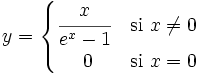Plantilla:Para ampliar: funcion derivada
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:38 26 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | + | {{Videotutoriales|titulo=Derivada de una función definida a trozos|enunciado= | |
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Derivada de una función definida a trozos | + | |titulo1=Tutorial |
| |duracion=10'49" | |duracion=10'49" | ||
| |sinopsis=Función derivada de una función definida a trozos. | |sinopsis=Función derivada de una función definida a trozos. | ||
| + | |||
| + | '''Nota:''' Requiere Flash Player y ver con Firefox | ||
| |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/09-funciones-a-trozos-y-reglas-de-derivacion-2#.WGOW5UZ9Vko | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/09-funciones-a-trozos-y-reglas-de-derivacion-2#.WGOW5UZ9Vko | ||
| }} | }} | ||
| + | ---- | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio | ||
| + | |duracion=6'26" | ||
| + | |sinopsis=Estudia la continuidad y derivabilidad de la función: | ||
| + | '''Nota:''' Requiere Flash Player y ver con Firefox | ||
| + | :<math>y = \begin{cases} \cfrac{x}{e^x-1} & \mbox{si }x \ne 0 \\ ~~~~0 & \mbox{si }x=0 \end{cases}</math> | ||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/06-derivabilidad-de-funciones/017-ejercicio-4 | ||
| + | }} | ||
| + | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1=Continuidad de las funciones derivables | |titulo1=Continuidad de las funciones derivables | ||
| |duracion=3'30" | |duracion=3'30" | ||
| |sinopsis=Teorema que relaciona la existencia de derivadas laterales y la continuidad de una función por la derecha y por la izquierda. | |sinopsis=Teorema que relaciona la existencia de derivadas laterales y la continuidad de una función por la derecha y por la izquierda. | ||
| + | |||
| + | '''Nota:''' Requiere Flash Player y ver con Firefox | ||
| |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/07-continuidad-de-las-funciones-derivables-2#.WGOVZEZ9Vko | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/07-continuidad-de-las-funciones-derivables-2#.WGOVZEZ9Vko | ||
| }} | }} | ||
Revisión actual
Continuidad de las funciones derivables (3'30") Sinopsis: Teorema que relaciona la existencia de derivadas laterales y la continuidad de una función por la derecha y por la izquierda.
Nota: Requiere Flash Player y ver con Firefox
