Plantilla:Regla de LHopital
De Wikipedia
| Revisión de 15:40 21 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Teorema_sin_demo|titulo=Regla de L'Hôpital|enunciado= | + | {{Teorema|titulo=Regla de L'Hôpital|enunciado= |
| Si al calcular <math>\lim_{x \to a} \cfrac{f(x)}{g(x)} </math> se presenta una indeterminación del tipo <math>\cfrac{0}{0}</math> ó <math>\cfrac{\infty}{\infty}</math>, y <math>\lim_{x \to a} \cfrac{f'(x)}{g'(x)}=l \, ; \ (l \in \mathbb{R})</math>, entonces <math>\lim_{x \to a} \cfrac{f(x)}{g(x)}=l </math>. | Si al calcular <math>\lim_{x \to a} \cfrac{f(x)}{g(x)} </math> se presenta una indeterminación del tipo <math>\cfrac{0}{0}</math> ó <math>\cfrac{\infty}{\infty}</math>, y <math>\lim_{x \to a} \cfrac{f'(x)}{g'(x)}=l \, ; \ (l \in \mathbb{R})</math>, entonces <math>\lim_{x \to a} \cfrac{f(x)}{g(x)}=l </math>. | ||
| Esto también es cierto si <math>x \to +\infty</math> o <math>x \to -\infty</math>. | Esto también es cierto si <math>x \to +\infty</math> o <math>x \to -\infty</math>. | ||
| + | |demo= | ||
| + | {{Video_enlace | ||
| + | |titulo1=Demostración | ||
| + | |duracion=16'32" | ||
| + | |sinopsis= | ||
| + | *Demostración de la regla de l'Hopital para el caso de indeterminación 0/0. | ||
| + | *Ejemplos de aplicación de la regla. | ||
| + | *Ejemplos en los que no se puede aplicar la regla por no verificarse las condiciones. | ||
| + | |url1=https://youtu.be/kwK1uEpmsE8 | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 9: | Línea 19: | ||
| |enunciado=Calcula: | |enunciado=Calcula: | ||
| :a)<math>\lim_{x \to 3} \cfrac{x^3-5x-12}{x^2+3x-18} </math> | :a)<math>\lim_{x \to 3} \cfrac{x^3-5x-12}{x^2+3x-18} </math> | ||
| + | |||
| :b)<math>\lim_{x \to +\infty} \cfrac{x^3}{2^x} </math> | :b)<math>\lim_{x \to +\infty} \cfrac{x^3}{2^x} </math> | ||
| + | |||
| + | :c)<math>\lim_{x \to 0} \cfrac{sen \, x}{x} </math> | ||
| |sol= | |sol= | ||
| a) <math>\lim_{x \to 3} \cfrac{x^3-5x-12}{x^2+3x-18} = ind. \left( \cfrac{0}{0} \right)</math> | a) <math>\lim_{x \to 3} \cfrac{x^3-5x-12}{x^2+3x-18} = ind. \left( \cfrac{0}{0} \right)</math> | ||
| Línea 30: | Línea 43: | ||
| <math>\lim_{x \to +\infty} \cfrac{6x}{2^x \, (ln \, 2)^2} =\lim_{x \to +\infty} \cfrac{6}{2^x \, (ln \, 2)^3}=0 </math> | <math>\lim_{x \to +\infty} \cfrac{6x}{2^x \, (ln \, 2)^2} =\lim_{x \to +\infty} \cfrac{6}{2^x \, (ln \, 2)^3}=0 </math> | ||
| + | |||
| + | ---- | ||
| + | c)<math>\lim_{x \to 0} \cfrac{sen \, x}{x} = \cfrac{sen \, 0}{0} = ind. \left( \cfrac{0}{0} \right) </math> | ||
| + | |||
| + | Aplicando la regla de L'Hôpital: | ||
| + | |||
| + | <math>\lim_{x \to 0} \cfrac{sen \, x}{x} = \lim_{x \to 0} \cfrac{cos \, x}{1} =\cfrac{cos \, 0}{1} = 1 </math> | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 35: | Línea 56: | ||
| {{p}} | {{p}} | ||
| {{Videos: Regla de LHopital}} | {{Videos: Regla de LHopital}} | ||
| + | {{Videos: Limites trigonométricos}} | ||
Revisión actual
Regla de L'Hôpital
Si al calcular 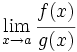 se presenta una indeterminación del tipo
se presenta una indeterminación del tipo 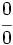 ó
ó 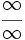 , y
, y 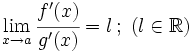 , entonces
, entonces 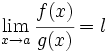 .
.
Esto también es cierto si  o
o 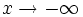 .
.
- Demostración de la regla de l'Hopital para el caso de indeterminación 0/0.
- Ejemplos de aplicación de la regla.
- Ejemplos en los que no se puede aplicar la regla por no verificarse las condiciones.
Ejercicio resuelto: Regla de L'Hôpital
Calcula:
- a)
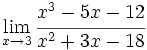
- b)
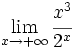
- c)
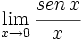
a) 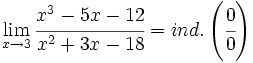
Aplicando la regla de L'Hôpital:
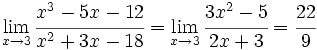
b) 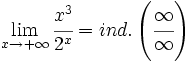
Aplicando la regla de L'Hôpital:
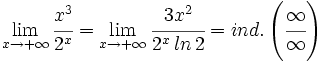
Aplicando la regla de L'Hôpital otra vez:
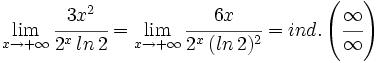
Y aplicando la regla de L'Hôpital una vez más:
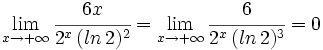
c)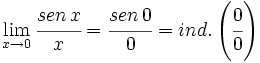
Aplicando la regla de L'Hôpital:
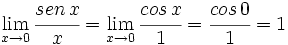
Regla de l'Hopital para los casos de indeterminación básicos. Ejemplos.
Regla de l'Hopital para todos los casos de indeterminación. Ejemplos.
Calcula: 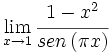
Calcula: 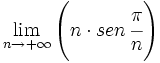
Calcula: 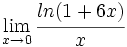
Calcula: 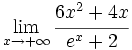
Calcula: 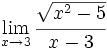
Calcula: 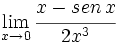
Calcula: 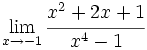
Regla de l'Hopital. Ejemplos en los que hay que aplicarla varias veces.
Calcula: 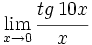
Calcula: 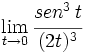
Calcula: 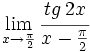
Calcula: 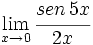
Calcula: 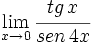
Calcula: 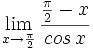
Calcula: 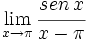
Calcula: 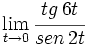
Calcula: 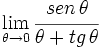
Calcula: 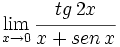
Calcula: 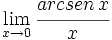
Calcula: