Plantilla:Limite en el infinito
De Wikipedia
| Revisión de 06:17 19 mar 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 21: | Línea 21: | ||
| |url1=https://youtu.be/RK3jbTI84hg?list=PLNQqRPuLTic-qVXmLl-4BSvfbCDN9Xt8W | |url1=https://youtu.be/RK3jbTI84hg?list=PLNQqRPuLTic-qVXmLl-4BSvfbCDN9Xt8W | ||
| }} | }} | ||
| - | {{Video_enlace_fonemato | + | {{Video_enlace_julioprofe |
| |titulo1=Tutorial 2 | |titulo1=Tutorial 2 | ||
| + | |duracion=12'33" | ||
| + | |sinopsis=4 ejemplos muy sencillos. | ||
| + | |url1=https://www.youtube.com/watch?v=P4Ui8wukDK0 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial 3 | ||
| |duracion=17'30" | |duracion=17'30" | ||
| |sinopsis=En este vídeo hablamos del límite de la función "f" cuando x → +∞; ya sea dicho límite finito, +∞ ó -∞. También hablamos del límite de "f" cuando x → -∞; ya sea dicho límite finito, +∞ ó -∞. | |sinopsis=En este vídeo hablamos del límite de la función "f" cuando x → +∞; ya sea dicho límite finito, +∞ ó -∞. También hablamos del límite de "f" cuando x → -∞; ya sea dicho límite finito, +∞ ó -∞. | ||
| Línea 28: | Línea 34: | ||
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Tutorial 3 (nivel superior) | + | |titulo1=Tutorial 4 (nivel superior) |
| |duracion=33'58" | |duracion=33'58" | ||
| |sinopsis=Definición rigurosa de límite de una función cuando x tiende a (+/-) infinito. | |sinopsis=Definición rigurosa de límite de una función cuando x tiende a (+/-) infinito. | ||
| |url1=https://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/02-limites-de-funciones/10-limites-en-el-infinito | |url1=https://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/02-limites-de-funciones/10-limites-en-el-infinito | ||
| - | }} | ||
| - | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplos | ||
| - | |duracion=12'33" | ||
| - | |sinopsis=4 ejemplos muy sencillos. | ||
| - | |url1=https://www.youtube.com/watch?v=P4Ui8wukDK0 | ||
| }} | }} | ||
| }} | }} | ||
| Línea 65: | Línea 65: | ||
| {{b}} | {{b}} | ||
| - | :e) <math>\lim_{x \to + \infty} f(x)= sen \, x = \mbox{ no existe por ser oscilante} </math> | + | :e) <math>\lim_{x \to + \infty} sen \, x = \mbox{ no existe por ser oscilante} </math> |
| - | :{{b4}}<math>\lim_{x \to - \infty} f(x)= sen \, x = \mbox{ no existe por ser oscilante} </math> | + | :{{b4}}<math>\lim_{x \to - \infty} sen \, x = \mbox{ no existe por ser oscilante} </math> |
| ---- | ---- | ||
| Haz uso de la siguiente escena de Geogebra para comprobar la solución: | Haz uso de la siguiente escena de Geogebra para comprobar la solución: | ||
Revisión actual
- Decimos que "
 tiende a + infinito" (
tiende a + infinito" (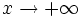 ) cuando
) cuando  toma valores positivos tan grandes como queramos.
toma valores positivos tan grandes como queramos.
- Decimos que "
 tiende a - infinito" (
tiende a - infinito" (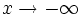 ) cuando
) cuando  toma valores negativos tan pequeños como queramos.
toma valores negativos tan pequeños como queramos.
- A veces te podrás encontrar también la expresión "
 tiende a infinito" (
tiende a infinito" (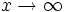 ) cuando
) cuando  tiende, indistintamente, a
tiende, indistintamente, a  o a
o a  , aunque también hay quien la usa en lugar de
, aunque también hay quien la usa en lugar de 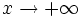 .
.
Los posibles comportamientos de una función cuando x tiende a  (o a
(o a  ) son los siguientes:
) son los siguientes:
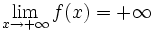 si cuando
si cuando  , los valores de
, los valores de  se hacen tan grandes que no se pueden acotar.
se hacen tan grandes que no se pueden acotar.
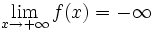 si cuando
si cuando  , los valores de
, los valores de  se hacen tan pequeños y negativos que no se pueden acotar.
se hacen tan pequeños y negativos que no se pueden acotar.
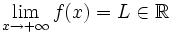 si cuando
si cuando  , los valores de
, los valores de  se hacen tan proximos a
se hacen tan proximos a 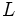 como se quiera.
como se quiera.
- En este caso se dice que la recta
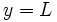 es una asíntota horizontal (A.H.) de la función.
es una asíntota horizontal (A.H.) de la función.
En estas tres definiciones se puede cambiar  por
por 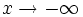 para obtener otras tres definiciones análogas.
para obtener otras tres definiciones análogas.
Idea gráfica del límite de una función cuando x tiende a infinito
4 ejemplos muy sencillos.
En este vídeo hablamos del límite de la función "f" cuando x → +∞; ya sea dicho límite finito, +∞ ó -∞. También hablamos del límite de "f" cuando x → -∞; ya sea dicho límite finito, +∞ ó -∞.
Definición rigurosa de límite de una función cuando x tiende a (+/-) infinito.
Ejemplo: Comportamiento de una función cuando x tiende a (+/-) infinito
Apoyándote en los conocimientos que tengas de la gráfica de las siguientes funciones, obten y comprueba el valor de sus límites en  y
y  , cuando éstos existan o tenga sentido calcularlos.
, cuando éstos existan o tenga sentido calcularlos.
- a)
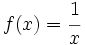 b)
b) 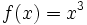 c)
c) 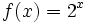 d)
d) 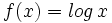 e)
e) 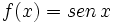
- a)
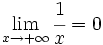 (La recta y=0 es una A.H. por
(La recta y=0 es una A.H. por  )
)
-
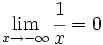 (La recta y=0 es una A.H. por
(La recta y=0 es una A.H. por  )
)
- b)
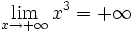
-
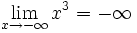
- c)
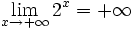
-
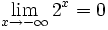 (La recta y=0 es una A.H. por
(La recta y=0 es una A.H. por  )
)
- d)
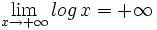
-
- e)
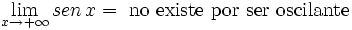
-
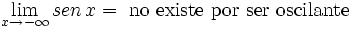
Haz uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.

