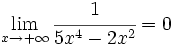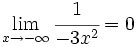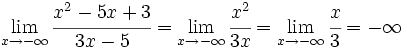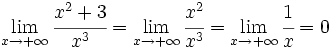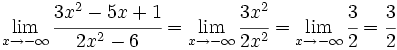Plantilla:Cálculo de límites en el infinito (1ºBach)
De Wikipedia
| Revisión de 11:05 18 dic 2016 Coordinador (Discusión | contribuciones) (→Límite de funciones racionales cuando x tiende a (+/-) infinito) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ejercicios y videotutoriales) |
||
| Línea 1: | Línea 1: | ||
| ==Comportamiento de una función cuando x tiende a (+/-) infinito== | ==Comportamiento de una función cuando x tiende a (+/-) infinito== | ||
| - | Los posibles comportamientos de una función cuando x tiende a <math> + \infty</math> (o a <math> - \infty</math>) son los siguientes: | + | {{limite en el infinito}} |
| - | {{p}} | + | |
| - | {{Caja_Amarilla|texto= | + | |
| - | *<math>\lim_{x \to +\infty} f(x)=+\infty</math> si cuando <math>x \to + \infty</math>, los valores de <math>f(x)\;</math> se hacen tan grandes que no se pueden acotar. | + | |
| - | *<math>\lim_{x \to +\infty} f(x)=-\infty</math> si cuando <math>x \to + \infty</math>, los valores de <math>f(x)\;</math> se hacen tan pequeños y negativos que no se pueden acotar. | + | |
| - | *<math>\lim_{x \to +\infty} f(x)=L \in \mathbb{R}</math> si cuando <math>x \to + \infty</math>, los valores de <math>f(x)\;</math> se hacen tan proximos a <math>L\;</math> como se quiera. En este caso se dice que la recta <math>y=L\;</math> es una '''asíntota horizontal''' (A.H.) de la función. | + | |
| - | {{p}} | + | |
| - | ---- | + | |
| - | En estas tres definiciones se puede cambiar <math>x \to +\infty</math> por <math>x \to -\infty</math> para obtener otras tres definiciones análogas. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo|titulo=Ejemplo: ''Comportamiento de una función cuando x tiende a (+/-) infinito''|enunciado= | + | |
| - | Apoyándote en los conocimientos que tengas de la gráfica de las siguientes funciones, obten y comprueba el valor de sus límites en <math>+ \infty</math> y <math>- \infty</math>, cuando éstos existan o tenga sentido calcularlos. | + | |
| - | :a) <math>f(x)= \cfrac{1}{x}</math>{{b4}}{{b4}}b) <math>f(x)= x^3\;</math>{{b4}}{{b4}}c) <math>f(x)= 2^x\;</math>{{b4}}{{b4}}d) <math>f(x)= log \, x</math>{{b4}}{{b4}}e) <math>f(x)= sen \, x </math> | + | |
| - | |sol= | + | |
| - | :a) <math>\lim_{x \to + \infty} \cfrac{1}{x}=0</math>{{b4}}(La recta y=0 es una A.H. por <math>+ \infty</math>) | + | |
| - | :{{b4}}<math>\lim_{x \to -\infty} \cfrac{1}{x}=0</math>{{b4}}(La recta y=0 es una A.H. por <math>- \infty</math>) | + | |
| - | {{p}} | + | |
| - | {{b}} | + | |
| - | + | ||
| - | :b) <math>\lim_{x \to + \infty} x^3= + \infty</math> | + | |
| - | :{{b4}}<math>\lim_{x \to - \infty} x^3= - \infty</math> | + | |
| - | {{p}} | + | |
| - | {{b}} | + | |
| - | + | ||
| - | :c) <math>\lim_{x \to + \infty} 2^x= + \infty</math> | + | |
| - | :{{b4}}<math>\lim_{x \to - \infty} 2^x= 0</math>{{b4}}(La recta y=0 es una A.H. por <math>- \infty</math>) | + | |
| - | {{p}} | + | |
| - | {{b}} | + | |
| - | + | ||
| - | :d) <math>\lim_{x \to + \infty} log \, x=+ \infty</math> | + | |
| - | :{{b4}}<math>\lim_{x \to - \infty} log \, x= \mbox{no tiene sentido plantearlo}</math> | + | |
| - | {{p}} | + | |
| - | {{b}} | + | |
| - | + | ||
| - | :e) <math>\lim_{x \to + \infty} f(x)= sen \, x = \mbox{ no existe por ser oscilante} </math> | + | |
| - | :{{b4}}<math>\lim_{x \to - \infty} f(x)= sen \, x = \mbox{ no existe por ser oscilante} </math> | + | |
| - | ---- | + | |
| - | Haz uso de la siguiente escena de Geogebra para comprobar la solución: | + | |
| - | + | ||
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás representar funciones definidas en hasta 4 trozos. | + | |
| - | |enlace=[https://ggbm.at/JCV99Kf8 Representador de funciones] | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
| Línea 58: | Línea 13: | ||
| ==Límite de funciones polinómicas cuando x tiende a (+/-) infinito== | ==Límite de funciones polinómicas cuando x tiende a (+/-) infinito== | ||
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=Sea <math>P(x)=a_nx^n+a_{n-1}x^{n-1}+ \cdots + a_1 x + a_0\;</math> una función polinómica en la variable x, de grado n. | + | {{Límite de funciones polinómicas cuando x tiende a infinito}} |
| - | Se cumple que: | + | ==Límite de funciones inversas de polinómicas cuando x tiende a (+/-) infinito== |
| + | {{Teorema_sin_demo|titulo=Proposición|enunciado=Sea <math>P(x)\;</math> una función polinómica en la variable x. Se cumple que: | ||
| - | *<math>\lim_{x \to + \infty} P(x)= \begin{cases} +\infty \ \ \mbox{si} \ \ a_n>0 \\ -\infty \ \ \mbox{si} \ \ a_n<0 \end{cases}</math> | + | *<math>\lim_{x \to + \infty} \cfrac{1}{P(x)}= 0</math>{{b4}}{{b4}}(lo mismo si <math>x \to - \infty</math>) |
| - | *<math>\lim_{x \to - \infty} P(x)= | + | }} |
| - | \begin{cases} | + | {{p}} |
| - | +\infty \ \ \mbox{si} \ \ a_n>0 \ \mbox{y n es par} | + | {{Ejemplo_simple|titulo=Ejemplos:|contenido= |
| - | \\ | + | *<math>\lim_{x \to + \infty} \cfrac{1}{5x^4-2x^2} = 0</math> |
| - | +\infty \ \ \mbox{si} \ \ a_n<0 \ \mbox{y n es impar} | + | |
| - | \\ | + | |
| - | -\infty \ \ \mbox{si} \ \ a_n<0 \ \mbox{y n es par} | + | |
| - | \\ | + | |
| - | -\infty \ \ \mbox{si} \ \ a_n>0 \ \mbox{y n es impar} | + | |
| - | \end{cases}</math> | + | *<math>\lim_{x \to - \infty} \cfrac{1}{-3x^2} = 0 </math> |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Observa cómo el valor del límite sólo depende del término de mayor grado del polinomio P(x). | + | {{Video_enlace_matefacil |
| + | |titulo1=Ejemplos | ||
| + | |duracion=15'59" | ||
| + | |sinopsis=Límites cuando x tiende a infinito de de una función inversa de polinómica. | ||
| + | |||
| + | |url1=https://youtu.be/wm-HUNf0y28?list=PL9SnRnlzoyX0o0z-YWbg6P3Pz9I0xlklS | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| - | *<math>\lim_{x \to + \infty} 5x^4-2x^2 = + \infty</math> | ||
| - | *<math>\lim_{x \to + \infty} -3x^4-2x^2 = - \infty</math> | + | ==Límite de funciones racionales cuando x tiende a (+/-) infinito== |
| + | {{Límite de funciones racionales cuando x tiende a infinito}} | ||
| + | {{p}} | ||
| + | ==Ejercicios y videotutoriales== | ||
| + | {{Videotutoriales|titulo=Operaciones con infinito y 0|enunciado= | ||
| + | {{Video_enlace_8cifras | ||
| + | |titulo1=Tutorial 1a | ||
| + | |duracion=6'38" | ||
| + | |sinopsis=Reglas para operar con infinito. Indeterminaciones. | ||
| - | *<math>\lim_{x \to - \infty} -2x^3-2x^2 = + \infty</math> | + | |url1=https://youtu.be/2dFx8LLjSQQ?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K |
| + | }} | ||
| + | {{Video_enlace_8cifras | ||
| + | |titulo1=Tutorial 1b | ||
| + | |duracion=6'07" | ||
| + | |sinopsis=Reglas para operar con infinito. Indeterminaciones. | ||
| - | *<math>\lim_{x \to - \infty} 5x^4-2x^2 = + \infty</math> | + | |url1=https://youtu.be/kTiavcG5xE4?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K |
| + | }} | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Comparación de infinitos|enunciado= | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Tutorial 1a | ||
| + | |duracion=14'10" | ||
| + | |sinopsis=Comparación de infinitos (exponenciales, polinómicas y logarítmicas) | ||
| - | *<math>\lim_{x \to - \infty} -2x^2-2x^2 = - \infty</math> | + | |url1=https://youtu.be/jeTPlVGA0_U?list=PLNQqRPuLTic-qVXmLl-4BSvfbCDN9Xt8W |
| + | }} | ||
| + | {{Video_enlace_8cifras | ||
| + | |titulo1=Tutorial 1b | ||
| + | |duracion=7'20" | ||
| + | |sinopsis=Comparación de infinitos: orden de un infinito (casos más sencillos) | ||
| - | *<math>\lim_{x \to - \infty} 2x^3-2x^2 = - \infty</math> | + | |url1=https://youtu.be/C-QW0QpkYlQ?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K |
| + | }} | ||
| + | {{Video_enlace_8cifras | ||
| + | |titulo1=Tutorial 1c | ||
| + | |duracion=7'18" | ||
| + | |sinopsis=Comparación de infinitos: orden de un infinito (casos más complejos) | ||
| + | |url1=https://youtu.be/GSqY4mm4hkw?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K | ||
| }} | }} | ||
| + | }} | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Límites cuando x tiende a -infinito | ||
| + | |duracion=6'48" | ||
| + | |sinopsis=Límites cuando x tiende a -infinito. Otra forma de hacerlos. | ||
| - | ==Límite de funciones inversas de polinómicas cuando x tiende a (+/-) infinito== | + | |url1=https://youtu.be/51l3p_mJyRc?list=PLNQqRPuLTic-qVXmLl-4BSvfbCDN9Xt8W |
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=Sea <math>P(x)\;</math> una función polinómica en la variable x. Se cumple que: | + | }} |
| + | ---- | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Ejercicios 1 | ||
| + | |duracion=12'45" | ||
| + | |sinopsis=Límites cuando x tiende a infinito de diferencias con radicales y límites de potencias. | ||
| - | *<math>\lim_{x \to + \infty} \cfrac{1}{P(x)}= 0</math> | + | |url1=https://youtu.be/k5GJeQZuDNw?list=PLNQqRPuLTic-qVXmLl-4BSvfbCDN9Xt8W |
| + | }} | ||
| + | {{Video_enlace_LaMejorAsesoríaEducativa | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=26'20" | ||
| + | |sinopsis=Ejercicios de límites de funciones racionales, polinómicas y radicales de racionales, cuando x tiende a infinito | ||
| - | *<math>\lim_{x \to - \infty} \cfrac{1}{P(x)}= 0</math> | + | |url1=https://youtu.be/_R8z7XRevHc?list=PLyC1b2B57_HFW-7Heqe9j0gMggFTSUSOZ |
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_8cifras |
| - | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | + | |titulo1=Ejercicio 3 |
| - | *<math>\lim_{x \to + \infty} \cfrac{1}{5x^4-2x^2} = 0</math> | + | |duracion=6'57" |
| + | |sinopsis=Límite con indeterminación infinito menos infinito: funciones racionales. | ||
| - | *<math>\lim_{x \to - \infty} \cfrac{1}{-3x^2} = 0 </math> | + | |url1=https://youtu.be/iigWu-aTWn4?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K |
| + | }} | ||
| + | {{Videotutoriales|titulo=Límite de funciones con radicales|enunciado= | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicio 1a | ||
| + | |duracion=9'50" | ||
| + | |sinopsis=Límite de raíces de funciones racionales en el infinito. | ||
| + | |url1=https://youtu.be/LBmXC7WkGoI?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn | ||
| }} | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicio 1b | ||
| + | |duracion=12'01" | ||
| + | |sinopsis=Límite de raíces de funciones racionales en el infinito. | ||
| - | ==Límite de funciones racionales cuando x tiende a (+/-) infinito== | + | |url1=https://youtu.be/MdCyLM4Kduk?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn |
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=Sea <math>\cfrac{P(x)}{Q(x)}=\cfrac{a_nx^n+a_{n-1}x^{n-1}+ \cdots + a_1 x + a_0}{b_m x^n+b_{m-1}x^{n-1}+ \cdots + b_1 x + b_0}\;</math> una función racional en la variable x. | + | }} |
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicio 1c | ||
| + | |duracion=10'00" | ||
| + | |sinopsis=Límite de raíces de funciones racionales en el infinito. | ||
| - | Se cumple que: | + | |url1=https://youtu.be/Qpc_NkjJ8kc?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn |
| + | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicio 1d | ||
| + | |duracion=14'49" | ||
| + | |sinopsis=Límite de raíces de funciones con radicales en el infinito. | ||
| - | :<math>\lim_{x \to + \infty} \cfrac{P(x)}{Q(x)}= \lim_{x \to + \infty} \cfrac{a_n x^n}{b_m x^m}</math> {{b4}}{{b4}}(lo mismo si <math>x \to - \infty</math>) | + | |url1=https://youtu.be/PO47o0ibDV4?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn |
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 2a | ||
| + | |duracion=4'14" | ||
| + | |sinopsis=Límite de funciones racionales con raíces en el infinito usando un método riguroso. | ||
| - | Tras simplificar esa fracción, se pueden dar los siguientes casos: | + | |url1=https://youtu.be/VluV3fxCySg?list=PL9SnRnlzoyX0o0z-YWbg6P3Pz9I0xlklS |
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 2b | ||
| + | |duracion=3'51" | ||
| + | |sinopsis=Límite de funciones racionales con raíces en el infinito usando un método riguroso. | ||
| - | *'''grado(P)>grado(Q):''' tras simplificar la fracción queda el límite de una función polinómica, que ya sabemos calcular y que sabemos que puede ser <math>+ \infty</math> ó <math>- \infty</math>. | + | |url1=https://youtu.be/YdEunJEwsoA?list=PL9SnRnlzoyX0o0z-YWbg6P3Pz9I0xlklS |
| - | *'''grado(P)=grado(Q):''' tras simplificar la fracción queda una constante, <math>\cfrac{a_n}{b_n}</math>, que es el valor del límite. | + | |
| - | *'''grado(P)<grado(Q):''' tras simplificar la fracción queda una función inversa de una polinómica, cuyo límite sabemos que vale 0. | + | |
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_matefacil |
| - | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | + | |titulo1=Ejercicio 2c |
| - | *<math>\lim_{x \to - \infty} \cfrac{x^2-5x+3}{3x-5} =\lim_{x \to - \infty} \cfrac{x^2}{3x} =\lim_{x \to - \infty} \cfrac{x}{3} = - \infty</math> | + | |duracion=6'46" |
| + | |sinopsis=Límite de funciones racionales con raíces en el infinito usando un método riguroso. | ||
| - | *<math>\lim_{x \to + \infty} \cfrac{x^2+3}{x^3} =\lim_{x \to + \infty} \cfrac{x^2}{x^3} =\lim_{x \to + \infty} \cfrac{1}{x} = 0</math> | + | |url1=https://youtu.be/jILqifoOxeE?list=PL9SnRnlzoyX0o0z-YWbg6P3Pz9I0xlklS |
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 2d | ||
| + | |duracion=7'45" | ||
| + | |sinopsis=Límite de funciones racionales con raíces en el infinito usando un método riguroso. | ||
| - | *<math>\lim_{x \to - \infty} \cfrac{3x^2-5x+1}{2x^2-6} =\lim_{x \to - \infty} \cfrac{3x^2}{2x^2} =\lim_{x \to - \infty} \cfrac{3}{2} = \cfrac{3}{2}</math> | + | |url1=https://youtu.be/403jr0WxYNo?list=PL9SnRnlzoyX0o0z-YWbg6P3Pz9I0xlklS |
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 2e | ||
| + | |duracion=5'14" | ||
| + | |sinopsis=Límite de funciones racionales con raíces en el infinito usando un método riguroso. | ||
| + | |url1=https://youtu.be/sCzBpMfYT_0?list=PL9SnRnlzoyX0o0z-YWbg6P3Pz9I0xlklS | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_matefacil |
| - | |titulo1=Límite de una función en el infinito | + | |titulo1=Ejercicio 2f |
| - | |duracion=17'30" | + | |duracion=5'39" |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis=Límite de funciones racionales con raíces en el infinito usando un método riguroso. |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0209.html | + | |
| + | |url1=https://youtu.be/mLNWhDXveuE?list=PL9SnRnlzoyX0o0z-YWbg6P3Pz9I0xlklS | ||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_matefacil |
| - | {{Video_enlace2 | + | |titulo1=Ejercicio 2g |
| - | |titulo1=Límite de un polinomio en el infinito | + | |duracion=5'44" |
| - | |duracion=9'59" | + | |sinopsis=Límite de funciones racionales con raíces en el infinito usando un método riguroso. |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0210.html | + | |url1=https://youtu.be/LuqmcGbardg?list=PL9SnRnlzoyX0o0z-YWbg6P3Pz9I0xlklS |
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_8cifras |
| - | {{Video_enlace2 | + | |titulo1=Ejercicio 3a |
| - | |titulo1=Límite de una función racional en el infinito | + | |duracion=6'32" |
| - | |duracion=11'23" | + | |sinopsis=Caso de racional con radicales. |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0211.html | + | |url1=https://youtu.be/w938VSKWEIk?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K |
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_8cifras |
| - | {{ejemplo2 | + | |titulo1=Tutorial 3b |
| - | |titulo=Ejemplos: ''Límite de una función racional en el infinito'' | + | |duracion=6'23" |
| - | |enunciado= | + | |sinopsis=Límite con indeterminación infinito menos infinito: funciones irracionales. |
| - | {{Video_enlace2 | + | |
| - | |titulo1=1. Ejemplos | + | |url1=https://youtu.be/aMZfTIOWVIQ?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K |
| - | |duracion=10'18" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0211_01.html | + | |
| }} | }} | ||
| - | {{Video_enlace2 | ||
| - | |titulo1=2. Ejemplos | ||
| - | |duracion=12'19" | ||
| - | |sinopsis=Video tutorial de matematicasbachiller.com | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0211_02.html | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Videotutoriales|titulo=Límite de funciones trigonométricas|enunciado= |
| - | |titulo1=3. Ejemplos | + | {{Video_enlace_profealex |
| - | |duracion=9'20" | + | |titulo1=Ejercicio 1 |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |duracion=5'52" |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0211_03.html | + | |sinopsis=Límite de raíces de funciones trigonométricas en el infinito. |
| + | |||
| + | |url1=https://youtu.be/SCbkQD9LcRs?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_profealex |
| - | |titulo1=4. Ejemplos | + | |titulo1=Ejercicio 2 |
| - | |duracion=11'14" | + | |duracion=8'06" |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis=Límite de raíces de funciones trigonométricas en el infinito. |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0211_04.html | + | |
| + | |url1=https://youtu.be/kqOPi_-gWjs?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_profealex |
| - | |titulo1=5. Ejemplos | + | |titulo1=Ejercicio 3 |
| - | |duracion=14'54" | + | |duracion=7'35" |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis=Límite de raíces de funciones trigonométricas en el infinito. |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0211_05.html | + | |
| + | |url1=https://youtu.be/Bjbreq2J48g?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_profealex |
| - | |titulo1=6. Ejemplos | + | |titulo1=Ejercicio 4 |
| - | |duracion=13'09" | + | |duracion=6'19" |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis=Límite de raíces de funciones trigonométricas en el infinito. |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0211_06.html | + | |
| + | |url1=https://youtu.be/pF-olTyz-0k?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_profealex |
| - | |titulo1=7. Ejemplos | + | |titulo1=Ejercicio 5 |
| - | |duracion=25'11" | + | |duracion=7'43" |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis=Límite de raíces de funciones trigonométricas en el infinito. |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0211_07.html | + | |
| + | |url1=https://youtu.be/qxfxyb6p14U?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn | ||
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_profealex |
| - | |titulo1=8. Ejemplos | + | |titulo1=Ejercicio 6 |
| - | |duracion=18'16" | + | |duracion=8'20" |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis=Límite de raíces de funciones trigonométricas en el infinito. |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0211_08.html | + | |
| + | |url1=https://youtu.be/Xq39rh0qe0Y?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn | ||
| }} | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=10'53" | ||
| + | |sinopsis=Límite de raíces de funciones trigonométricas en el infinito. | ||
| + | |||
| + | |url1=https://youtu.be/ZW1D_yhj8ag?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn | ||
| + | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=4'38" | ||
| + | |sinopsis=Límite de raíces de funciones trigonométricas en el infinito. | ||
| + | |||
| + | |url1=https://youtu.be/vWQf6Ydowuk?list=PLeySRPnY35dG9t51yT4nCwQEtWwCwvBwn | ||
| + | }} | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Indeterminación 1 elevado a infinito (número e) (Nivel superior)|enunciado= | ||
| + | {{Video_enlace_8cifras | ||
| + | |titulo1=Ejercicio 1a | ||
| + | |duracion=9'25" | ||
| + | |sinopsis=Indeterminación 1 elevado a infinito. | ||
| + | |url1=https://youtu.be/kP1WVXUXR94?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K | ||
| + | }} | ||
| + | {{Video_enlace_8cifras | ||
| + | |titulo1=Ejercicio 1b | ||
| + | |duracion=4'27" | ||
| + | |sinopsis=Mismo ejercicio que el anterior por otro método más corto que requiere el uso de una fórmula. | ||
| + | |url1=https://youtu.be/iSvsDVmhe4U?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K | ||
| + | }} | ||
| + | {{Video_enlace_8cifras | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=5'08" | ||
| + | |sinopsis=Demostración de la fórmula usada en el ejercicio anterior. | ||
| + | |url1=https://youtu.be/YcD3cFKMDXU?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K | ||
| + | }} | ||
| + | |||
| }} | }} | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
Revisión actual
Comportamiento de una función cuando x tiende a (+/-) infinito
- Decimos que "
 tiende a + infinito" (
tiende a + infinito" (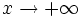 ) cuando
) cuando  toma valores positivos tan grandes como queramos.
toma valores positivos tan grandes como queramos.
- Decimos que "
 tiende a - infinito" (
tiende a - infinito" (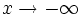 ) cuando
) cuando  toma valores negativos tan pequeños como queramos.
toma valores negativos tan pequeños como queramos.
- A veces te podrás encontrar también la expresión "
 tiende a infinito" (
tiende a infinito" (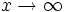 ) cuando
) cuando  tiende, indistintamente, a
tiende, indistintamente, a  o a
o a  , aunque también hay quien la usa en lugar de
, aunque también hay quien la usa en lugar de 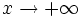 .
.
Los posibles comportamientos de una función cuando x tiende a  (o a
(o a  ) son los siguientes:
) son los siguientes:
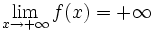 si cuando
si cuando  , los valores de
, los valores de  se hacen tan grandes que no se pueden acotar.
se hacen tan grandes que no se pueden acotar.
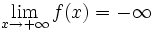 si cuando
si cuando  , los valores de
, los valores de  se hacen tan pequeños y negativos que no se pueden acotar.
se hacen tan pequeños y negativos que no se pueden acotar.
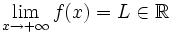 si cuando
si cuando  , los valores de
, los valores de  se hacen tan proximos a
se hacen tan proximos a 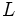 como se quiera.
como se quiera.
- En este caso se dice que la recta
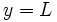 es una asíntota horizontal (A.H.) de la función.
es una asíntota horizontal (A.H.) de la función.
En estas tres definiciones se puede cambiar  por
por 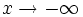 para obtener otras tres definiciones análogas.
para obtener otras tres definiciones análogas.
Idea gráfica del límite de una función cuando x tiende a infinito
4 ejemplos muy sencillos.
En este vídeo hablamos del límite de la función "f" cuando x → +∞; ya sea dicho límite finito, +∞ ó -∞. También hablamos del límite de "f" cuando x → -∞; ya sea dicho límite finito, +∞ ó -∞.
Definición rigurosa de límite de una función cuando x tiende a (+/-) infinito.
Ejemplo: Comportamiento de una función cuando x tiende a (+/-) infinito
Apoyándote en los conocimientos que tengas de la gráfica de las siguientes funciones, obten y comprueba el valor de sus límites en  y
y  , cuando éstos existan o tenga sentido calcularlos.
, cuando éstos existan o tenga sentido calcularlos.
- a)
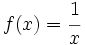 b)
b) 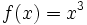 c)
c) 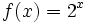 d)
d) 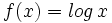 e)
e) 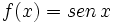
- a)
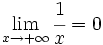 (La recta y=0 es una A.H. por
(La recta y=0 es una A.H. por  )
)
-
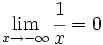 (La recta y=0 es una A.H. por
(La recta y=0 es una A.H. por  )
)
- b)
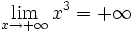
-
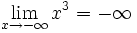
- c)
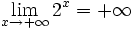
-
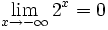 (La recta y=0 es una A.H. por
(La recta y=0 es una A.H. por  )
)
- d)
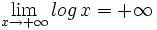
-
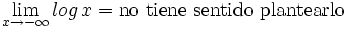
- e)
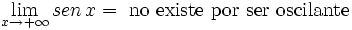
-
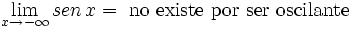
Haz uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
Ejercicios propuestos
|
Ejercicios propuestos: Comportamiento de una función cuando x tiende a (+/-) infinito |
Límite de funciones polinómicas cuando x tiende a (+/-) infinito
Observa cómo el valor del límite sólo depende del término de mayor grado del polinomio P(x).
Al calcular el límite de un polinomio en el infinito (x → +∞ ó x → -∞) sólo debes preocuparte del sumando de mayor grado, pues es él quien corta el bacalao.
Otra forma de calcular el límite de un polinomio en el infinito (x → +∞ ó x → -∞). También se incluyen otros casos de funciones radicales que tienen un tratamiento similar.
Ejercicios de límites de funciones polinómicas.
Ejercicios de límites de funciones polinómicas.
Límite de funciones inversas de polinómicas cuando x tiende a (+/-) infinito
Límites cuando x tiende a infinito de de una función inversa de polinómica.
Límite de funciones racionales cuando x tiende a (+/-) infinito
Proposición
Consideremos la función racional en la variable x, ya simplificada:
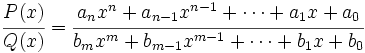
Se cumple que:
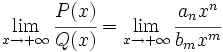 (análogamente si
(análogamente si 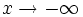 )
)Se pueden dar los siguientes casos:
- grado(P) > grado(Q): tras simplificar la fracción queda el límite de una función polinómica, que ya sabemos calcular, y que sabemos que puede ser
 ó
ó  .
.
- grado(P ) = grado(Q): tras simplificar la fracción queda una constante,
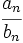 , que es el valor del límite.
, que es el valor del límite.
- grado(P) < grado(Q): tras simplificar la fracción queda una función inversa de una polinómica, cuyo límite sabemos que vale 0.
Límites cuando x tiende a infinito de cocientes de polinomios (método rápido) y diferencias de expresiones infinitas.
Límite de funciones racionales y de raíces de funciones racionales.
Caso 1: denominador con grado mayor que el numerador.
Caso 2: denominador con grado igual que el numerador.
Caso 3: denominador con grado menor que el numerador.
Para calcular el límite de un cociente de polinomios cuando x → +∞ o cuando x → -∞, dividimos numerador y denominador por la mayor potencia de "x" que aparezca en el denominador.
- Si numerador y denominador son de igual grado, el límite es el cociente de los coeficientes de los términos de mayor grado del numerador y el denominador.
- Si el numerador es de menor grado que el denominador, el límite es 0.
- Si el numerador es de mayor grado que el denominador, el límite es +∞ ó -∞ según que el numerador y el denominador tengan igual signo o no.
Calcula: 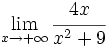
Calcula: 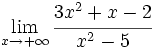
Calcula: 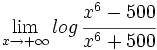
Límite de funciones racionales sencillas en el infinito.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Ejercicios y videotutoriales
Reglas para operar con infinito. Indeterminaciones.
Reglas para operar con infinito. Indeterminaciones.
Comparación de infinitos (exponenciales, polinómicas y logarítmicas)
Comparación de infinitos: orden de un infinito (casos más sencillos)
Comparación de infinitos: orden de un infinito (casos más complejos)
Límites cuando x tiende a -infinito. Otra forma de hacerlos.
Límites cuando x tiende a infinito de diferencias con radicales y límites de potencias.
Ejercicios de límites de funciones racionales, polinómicas y radicales de racionales, cuando x tiende a infinito
Límite con indeterminación infinito menos infinito: funciones racionales.
Límite de raíces de funciones racionales en el infinito.
Límite de raíces de funciones racionales en el infinito.
Límite de raíces de funciones racionales en el infinito.
Límite de raíces de funciones con radicales en el infinito.
Límite de funciones racionales con raíces en el infinito usando un método riguroso.
Límite de funciones racionales con raíces en el infinito usando un método riguroso.
Límite de funciones racionales con raíces en el infinito usando un método riguroso.
Límite de funciones racionales con raíces en el infinito usando un método riguroso.
Límite de funciones racionales con raíces en el infinito usando un método riguroso.
Límite de funciones racionales con raíces en el infinito usando un método riguroso.
Límite de funciones racionales con raíces en el infinito usando un método riguroso.
Caso de racional con radicales.
Límite con indeterminación infinito menos infinito: funciones irracionales.
Límite de raíces de funciones trigonométricas en el infinito.
Límite de raíces de funciones trigonométricas en el infinito.
Límite de raíces de funciones trigonométricas en el infinito.
Límite de raíces de funciones trigonométricas en el infinito.
Límite de raíces de funciones trigonométricas en el infinito.
Límite de raíces de funciones trigonométricas en el infinito.
Límite de raíces de funciones trigonométricas en el infinito.
Límite de raíces de funciones trigonométricas en el infinito.
Indeterminación 1 elevado a infinito.
Mismo ejercicio que el anterior por otro método más corto que requiere el uso de una fórmula.
Demostración de la fórmula usada en el ejercicio anterior.
Ejercicios propuestos
|
Ejercicios propuestos: Cálculo de límites cuando x tiende a (+/-) infinito |
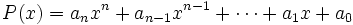 una función polinómica en la variable x, de grado n.
una función polinómica en la variable x, de grado n.
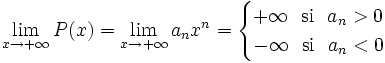
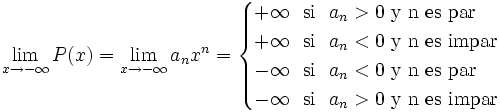
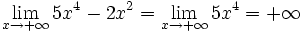
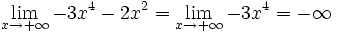
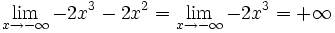
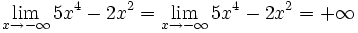
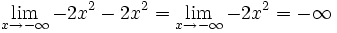
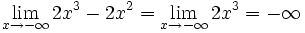
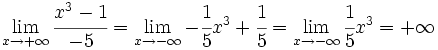
 una función polinómica en la variable x. Se cumple que:
una función polinómica en la variable x. Se cumple que:
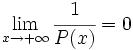 (lo mismo si
(lo mismo si