Plantilla:Ramas infinitas. Asíntotas
De Wikipedia
| Revisión de 07:39 2 abr 2020 Coordinador (Discusión | contribuciones) (→Estudio de las asíntotas de una función) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Estudio de las asíntotas de una función) |
||
| Línea 155: | Línea 155: | ||
| }} | }} | ||
| {{Video_enlace_8cifras | {{Video_enlace_8cifras | ||
| - | |titulo1=Tutorial 2a | + | |titulo1=Tutorial 2a (A.V.) |
| |duracion=9'04" | |duracion=9'04" | ||
| |sinopsis=Estudio de las asíntotas verticales de una función. | |sinopsis=Estudio de las asíntotas verticales de una función. | ||
| Línea 161: | Línea 161: | ||
| }} | }} | ||
| {{Video_enlace_8cifras | {{Video_enlace_8cifras | ||
| - | |titulo1=Tutorial 2b | + | |titulo1=Tutorial 2b (A.H.) |
| |duracion=9'03" | |duracion=9'03" | ||
| |sinopsis=Estudio de las asíntotas horizontales de una función. | |sinopsis=Estudio de las asíntotas horizontales de una función. | ||
| Línea 167: | Línea 167: | ||
| }} | }} | ||
| {{Video_enlace_8cifras | {{Video_enlace_8cifras | ||
| - | |titulo1=Tutorial 2c | + | |titulo1=Tutorial 2c (A.O.) |
| |duracion=7'42" | |duracion=7'42" | ||
| |sinopsis=Estudio de las asíntotas oblicuas de una función racional (Introducción). | |sinopsis=Estudio de las asíntotas oblicuas de una función racional (Introducción). | ||
| Línea 173: | Línea 173: | ||
| }} | }} | ||
| {{Video_enlace_8cifras | {{Video_enlace_8cifras | ||
| - | |titulo1=Tutorial 2d | + | |titulo1=Tutorial 2d (A.O.) |
| |duracion=7'32" | |duracion=7'32" | ||
| |sinopsis=Estudio de las asíntotas oblicuas de una función racional. | |sinopsis=Estudio de las asíntotas oblicuas de una función racional. | ||
| Línea 179: | Línea 179: | ||
| }} | }} | ||
| {{Video_enlace_8cifras | {{Video_enlace_8cifras | ||
| - | |titulo1=Tutorial 2e | + | |titulo1=Tutorial 2e (A.O.) |
| |duracion=8'05" | |duracion=8'05" | ||
| |sinopsis=Estudio de las asíntotas oblicuas de una función no racional. | |sinopsis=Estudio de las asíntotas oblicuas de una función no racional. | ||
| |url1=https://youtu.be/SHlZHxOtNx4?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K | |url1=https://youtu.be/SHlZHxOtNx4?list=PLpbLLqs33gIkbfeAzPddpOc6wnOu309-K | ||
| }} | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Ejemplos | ||
| + | |duracion=30'17" | ||
| + | |sinopsis=Estudia las asíntotas de las siguientes funciones: | ||
| + | #<math>\cfrac{x}{x^2-4}\;</math> | ||
| + | #<math>\cfrac{3x^2}{x^2+9}\;</math> | ||
| + | #<math>\cfrac{x^3+2x^2+x-3}{x^2-1}\;</math> | ||
| + | #<math>\cfrac{x^3-2}{2x+1}\;</math> | ||
| + | #<math>\cfrac{x^3-4x}{x+2}\;</math> | ||
| + | |||
| + | |url1=https://youtu.be/jc29ZOVapDQ | ||
| + | }} | ||
| {{Wolfram: Tendencias de una funcion}} | {{Wolfram: Tendencias de una funcion}} | ||
Revisión actual
Una función presenta una rama infinita si presenta una asíntota o una rama parabólica.
Pasamos a definir asíntota y rama parabólica.
Tabla de contenidos |
Asíntota
Una asíntota es una recta hacia la que se acerca la gráfica de una función, tanto como se quiera, a medida que la variable independiernte se aproxima a un punto, a  o a
o a  .
.
Hay tres tipos:
- Asíntota vertical (A.V.)
- Asíntota horizontal (A.H.)
- Asíntota oblicua (A.O.)
Nota: La función nunca puede cortar una A.V., pero si puede cortar a una A.H. o a una A.O.
Asíntotas. Tipos.
Asíntota vertical
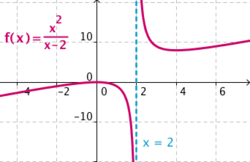
Una función Nota: Se pueden dar las dos condiciones o una sola de ellas. Veamos cómo la función En efecto, Haz uso de la siguiente escena de Geogebra para comprobar la solución: En esta escena podrás representar funciones definidas en hasta 4 trozos. | Asíntota vertical: x = 2
|
Asíntota horizontal
Una función 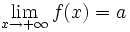 o bien, 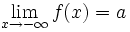 Nota: Se pueden dar las dos condiciones o una sola de ellas. Veamos cómo la función En efecto, Haz uso de la siguiente escena de Geogebra para comprobar la solución: En esta escena podrás representar funciones definidas en hasta 4 trozos. | Asíntota horizontal: y = 1
|
Asíntota oblicua
Una función ![\lim_{x \to +\infty} [f(x)-(mx+n)]= 0](/wikipedia/images/math/b/4/f/b4f57eb5b14023e40e6485b640fd5691.png) o bien, ![\lim_{x \to -\infty} [f(x)-(mx+n)]= 0](/wikipedia/images/math/d/c/1/dc195dc202ab07f6f60038a1570d06b3.png) Nota: Se pueden dar las dos condiciones o una sola de ellas. Para calcular los coeficientes
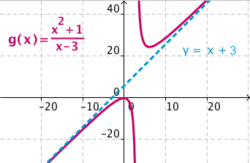
Veamos cómo la función En efecto, sea Para Haz uso de la siguiente escena de Geogebra para comprobar la solución: En esta escena podrás representar funciones definidas en hasta 4 trozos. | Asíntota oblicua: y = x + 3
|
Rama parabólica
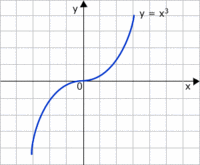
Una función 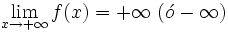 o bien, 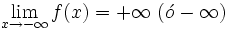 | Ramas parabólicas
|
Las funciones exponenciales, las polinómicas de grado mayor que 1, las logarítmicas y las irracionales tienen ramas parabólicas. Las dos primeras tienen un crecimiento/decrecimiento más rápido que las dos últimas.
Estudio de las asíntotas de una función
Asíntotas. Conceptos básicos. Ejemplos.
Estudio de las asíntotas verticales de una función.
Estudio de las asíntotas horizontales de una función.
Estudio de las asíntotas oblicuas de una función racional (Introducción).
Estudio de las asíntotas oblicuas de una función racional.
Estudio de las asíntotas oblicuas de una función no racional.
Estudia las asíntotas de las siguientes funciones:
|
Actividad: Tendencia de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
 presenta en
presenta en  una asíntota vertical (A.V.) si ocurre alguna, o ambas, de estas dos cosas:
una asíntota vertical (A.V.) si ocurre alguna, o ambas, de estas dos cosas:
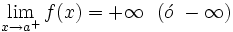
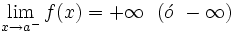
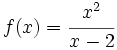 presenta una A.V. en
presenta una A.V. en 
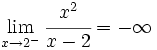
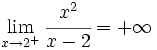
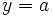 si:
si:
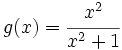 presenta una A.H. en
presenta una A.H. en 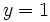
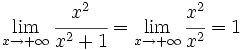
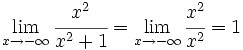

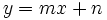 si:
si:
 y
y  de la asíntota, se procederá de la siguiente manera:
de la asíntota, se procederá de la siguiente manera:
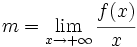 (o bien, con
(o bien, con 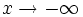 )
)
![n=\lim_{x \to +\infty} [f(x)-mx]](/wikipedia/images/math/c/d/7/cd758129321f1a26b36d644470fd76f5.png) (o bien, con
(o bien, con 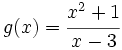 presenta una A.O. en
presenta una A.O. en 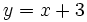
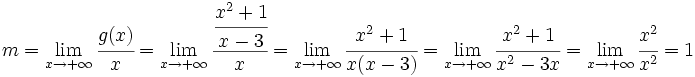
![n=\lim_{x \to 1^+} [g(x)-x]= \lim_{x \to +\infty} \left[\cfrac{x^2+1}{x-3}-x \right]= \lim_{x \to +\infty} \cfrac{x^2+1-x^2+3x}{x-3}= \lim_{x \to +\infty} \cfrac{3x+1}{x-3}= \lim_{x \to +\infty} \cfrac{3x}{x}= 3](/wikipedia/images/math/5/5/e/55e95a0bb6413ed7aa2ce396d251d30d.png)
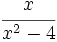
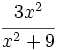
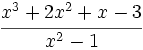
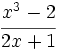
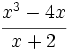
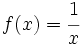 . cuando
. cuando  se hace infinitamente grande.
se hace infinitamente grande.

