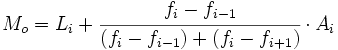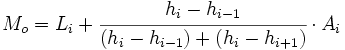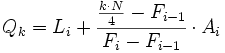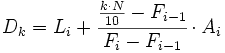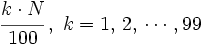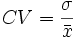Plantilla:Parámetros estadísticos
De Wikipedia
| Revisión de 07:37 4 ago 2017 Coordinador (Discusión | contribuciones) (→Media) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ejercicios y videotutoriales) |
||
| Línea 6: | Línea 6: | ||
| ===Moda=== | ===Moda=== | ||
| {{Moda}} | {{Moda}} | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Cálculo de la moda con datos agrupados en intervalos|enunciado= | ||
| + | |||
| + | Llamemos '''intervalo modal''' al que tiene mayor frecuencia absoluta y consideremos dos casos: | ||
| + | |||
| + | *Si todos los intervalos tienen la '''misma amplitud''', entonces la moda viene dada por la siguiente fórmula: | ||
| + | <br> | ||
| + | {{caja|contenido=<math>M_o=L_i+\cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i</math>}} | ||
| + | <br> | ||
| + | :*<math>L_i\;</math>: Extremo inferior del intervalo modal : | ||
| + | |||
| + | :*<math>f_i\;: </math> Frecuencia absoluta del intervalo modal. | ||
| + | |||
| + | :*<math>f_{i-1}\;: </math> Frecuencia absoluta del intervalo anterior al modal. | ||
| + | |||
| + | :*<math>f_{i+1}\;: </math> Frecuencia absoluta del intervalo posterior al modal. | ||
| + | |||
| + | :*<math>A_i\;</math>: Amplitud de los intervalos. | ||
| + | <br> | ||
| + | *Si todos los intervalos '''no tienen la misma amplitud''', entonces la moda viene dada por la siguiente fórmula: | ||
| + | <br> | ||
| + | {{caja|contenido=<math>M_o=L_i+\cfrac{h_i-h_{i-1}}{(h_i-h_{i-1})+(h_i-h_{i+1})}\cdot A_i</math>}} | ||
| + | <br> | ||
| + | {{b4}}{{b}}donde <math>h_i=\cfrac{f_i}{A_i}</math> son las alturas de cada intervalo. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Moda|enunciado= | {{Videotutoriales|titulo=Moda|enunciado= | ||
| Línea 30: | Línea 55: | ||
| }} | }} | ||
| }} | }} | ||
| + | {{Web_enlace_vitutor | ||
| + | |descripcion=La moda. Ejemplos. | ||
| + | |enlace=[http://www.vitutor.com/estadistica/descriptiva/a_8.html Moda] | ||
| + | }} | ||
| + | {{Ejercicios_vitutor | ||
| + | |descripcion=Ejercicios resueltos sobre el cálculo de la moda. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/d_4.html | ||
| + | |titulo1=Moda | ||
| + | }} | ||
| + | |||
| {{p}} | {{p}} | ||
| - | ===Media=== | + | ===Media aritmética=== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Se define la '''media''' como la suma de todos los datos dividida por el número de datos. Se representa por <math> \bar x\ </math>. | + | Se define la '''media aritmética''' como la suma de todos los datos dividida por el número de datos. Se representa por <math> \bar x\ </math>.}} |
| - | + | {{p}} | |
| + | {{Teorema_sin_demo|titulo=Cálculo de la media aritmética|enunciado= | ||
| *Para '''datos no agrupados''', la media se calcula como sigue: | *Para '''datos no agrupados''', la media se calcula como sigue: | ||
| <center> | <center> | ||
| - | <math> \bar x\ </math> = <math>\frac{x_1 + x_2 + ....+x_N} {N}={\sum_{i=1}^N x_i \over N} </math></center> | + | <math> \bar x\ </math> = <math>\frac{x_1 + x_2 + ....+x_N} {N}=\cfrac{\sum_{i=1}^N x_i}{N} </math></center> |
| - | :donde <math>N = num.\ total\ de\ individuos = \sum_{i=1}^N f_i</math>. | + | :donde <math>N = \sum_{i=1}^N f_i</math> es el número total de datos observados. |
| {{p}} | {{p}} | ||
| Línea 50: | Línea 86: | ||
| </center> | </center> | ||
| - | *Para el caso de '''datos agrupados por intervalos''', el cálculo se hace de la misma forma pero utilizando como <math> x_i</math> las '''marcas de clase''', que son los valores centrales de cada intervalo (media aritmética de los extremos de cada intervalo). | + | *Para el caso de '''datos agrupados por intervalos''', el cálculo se hace de la misma forma pero utilizando como <math> x_i\;</math> las '''marcas de clase''', que son los valores centrales de cada intervalo (media aritmética de los extremos de cada intervalo). |
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Media aritmética|enunciado= | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=7´34" | ||
| + | |url1=https://www.youtube.com/watch?v=2WPfO7kW1WQ&list=PL5AED12B3B3AA32D3&index=4 | ||
| + | |sinopsis=Media aritmética correspondiente a una muestra con datos agrupados o no agrupados. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 1 (datos no agrupados) | ||
| + | |duracion=7'58" | ||
| + | |sinopsis=Cálculo de la media para datos no agrupados. | ||
| + | |url1=https://www.youtube.com/watch?v=XiBEQ2QGu0E | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 2 (datos agrupados) | ||
| + | |duracion=16'45" | ||
| + | |sinopsis=Cálculo de la media para datos agrupados con o sin intervalos. | ||
| + | |url1=https://www.youtube.com/watch?v=PMo3Ydydats | ||
| + | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Media aritmética|enunciado= | ||
| {{AI_cidead | {{AI_cidead | ||
| - | |titulo1=Media | + | |titulo1=Actividad 1 |
| - | |descripcion=Actividades en la que podrás aprender a calcular la media de una distribución estadística. | + | |descripcion=Actividades en la que podrás aprender a calcular la media aritmética de una distribución estadística. |
| |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_3a.htm | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_3a.htm | ||
| }} | }} | ||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Media (pocos datos) | + | |titulo1=Actividad 2a (datos no agrupados) |
| - | |descripcion=Ejemplos de cálculo de medias de un conjunto de pocos datos. | + | |descripcion=Ejemplos de cálculo de medias aritméticas de un conjunto de datos no agrupados. |
| |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta4.htm | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta4.htm | ||
| }} | }} | ||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Autoevaluación: ''Media (pocos datos)'' | + | |titulo1=Actividad 2b (datos no agrupados) |
| - | |descripcion=Actividades para que practiques el cálculo de medias de un conjunto de pocos datos. | + | |
| - | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta4_aut.htm | + | |
| - | }} | + | |
| - | {{AI_descartes | + | |
| - | |titulo1=Media (muchos datos) | + | |
| - | |descripcion=Ejemplos de cálculo de medias de un conjunto de muchos datos agrupados o no por intervalos. | + | |
| - | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta5.htm | + | |
| - | }} | + | |
| - | {{AI_descartes | + | |
| - | |titulo1=Autoevaluación: ''Media (muchos datos)'' | + | |
| - | |descripcion=Actividades para que practiques el cálculo de medias de un conjunto de muchos datos agrupados o no por intervalos. | + | |
| - | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta5_aut.htm | + | |
| - | }} | + | |
| - | {{AI_descartes | + | |
| - | |titulo1=Actividad 1: ''Media (Variable discreta)'' | + | |
| |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/media_est.htm | |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/media_est.htm | ||
| |descripcion=Calcula en tu cuaderno la media para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | |descripcion=Calcula en tu cuaderno la media para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | ||
| Línea 99: | Línea 143: | ||
| #¿Cuál es el mayor valor que puede tomar la media? Justifica la respuesta. | #¿Cuál es el mayor valor que puede tomar la media? Justifica la respuesta. | ||
| }} | }} | ||
| + | |||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Actividad 2: ''Media (Variable continua)'' | + | |titulo1=Actividad 3a (datos agrupados) |
| + | |descripcion=Ejemplos de cálculo de medias de un conjunto de muchos datos agrupados o no por intervalos. | ||
| + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta5.htm | ||
| + | }} | ||
| + | {{AI_descartes | ||
| + | |titulo1=Actividad 3b (datos agrupados) | ||
| |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/media_est.htm | |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/media_est.htm | ||
| |descripcion=Calcula en tu cuaderno la media para el ejemplo de las estaturas: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, agrupando los datos en intervalos. Una vez que lo tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | |descripcion=Calcula en tu cuaderno la media para el ejemplo de las estaturas: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, agrupando los datos en intervalos. Una vez que lo tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | ||
| Línea 119: | Línea 169: | ||
| }} | }} | ||
| - | {{p}} | + | {{AI_descartes |
| - | {{Videotutoriales|titulo=Media|enunciado= | + | |titulo1=Autoevaluación 1a (datos no agrupados) |
| - | {{Video_enlace_fonemato | + | |descripcion=Actividades para que practiques el cálculo de medias aritméticas de un conjunto de datos no agrupados. |
| - | |titulo1=Tutorial | + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta4_aut.htm |
| - | |duracion=7´34" | + | |
| - | |url1=https://www.youtube.com/watch?v=2WPfO7kW1WQ&list=PL5AED12B3B3AA32D3&index=4 | + | |
| - | |sinopsis=Media aritmética correspondiente a una muestra con datos agrupados o no agrupados. | + | |
| }} | }} | ||
| - | ---- | + | {{AI_descartes |
| - | {{Video_enlace_abel | + | |titulo1=Autoevaluación 1b (datos agrupados)'' |
| - | |titulo1=Ejemplo 1 (datos no agrupados) | + | |descripcion=Actividades para que practiques el cálculo de medias de un conjunto de muchos datos agrupados o no por intervalos. |
| - | |duracion=7'58" | + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta5_aut.htm |
| - | |sinopsis=Cálculo de la media para datos no agrupados. | + | |
| - | |url1=https://www.youtube.com/watch?v=XiBEQ2QGu0E | + | |
| }} | }} | ||
| - | {{p}} | + | {{AI_vitutor |
| - | {{Video_enlace_abel | + | |descripcion=Ejercicios de autoevaluación sobre la media aritmética. |
| - | |titulo1=Ejemplo 2 (datos agrupados con o sin intervalos) | + | |url1=http://www.vitutor.com/estadistica/descriptiva/a_10_e.html |
| - | |duracion=16'45" | + | |titulo1=Autoevaluación 2 |
| - | |sinopsis=Cálculo de la media para datos agrupados con o sin intervalos. | + | |
| - | |url1=https://www.youtube.com/watch?v=PMo3Ydydats | + | |
| }} | }} | ||
| }} | }} | ||
| + | {{Web_enlace_vitutor | ||
| + | |descripcion=La media aritmética. Ejemplos. | ||
| + | |enlace=[http://www.vitutor.com/estadistica/descriptiva/a_10.html Media aritmética] | ||
| + | }} | ||
| + | {{Ejercicios_vitutor | ||
| + | |descripcion=Ejercicios resueltos sobre la media aritmética. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/d_6.html | ||
| + | |titulo1=Media aritmética | ||
| + | }} | ||
| + | |||
| + | |||
| {{p}} | {{p}} | ||
| Línea 149: | Línea 203: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | + | {{Teorema_sin_demo|titulo=Cálculo de la mediana|enunciado= |
| Para calcular la mediana es necesario que los datos estén ordenados de menor a mayor. Se pueden dar los siguientes casos: | Para calcular la mediana es necesario que los datos estén ordenados de menor a mayor. Se pueden dar los siguientes casos: | ||
| - | *''' Datos no agrupados''' o '''agrupados puntualmente''': Si hay un número impar de datos observados, habrá un sólo valor central, mientras que si hay un número par de datos habrá que hallar la media de los dos valores centrales. En el caso de datos agrupados puntualmente deberemos guiarnos con las frecuencias absolutas. | + | *''' Datos no agrupados''' o '''agrupados puntualmente''': Si hay un número impar de datos observados, habrá un sólo valor central, mientras que si hay un número par de datos habrá que hallar la media de los dos valores centrales. En el caso de datos agrupados puntualmente deberemos guiarnos con las frecuencias acumuladas. |
| *'''Datos agrupados por intervalos''': La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas. Es decir tenemos que buscar el intervalo en el que se encuentre <math>\cfrac{N}{2}</math>. Luego calculamos la mediana según la siguiente fórmula: | *'''Datos agrupados por intervalos''': La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas. Es decir tenemos que buscar el intervalo en el que se encuentre <math>\cfrac{N}{2}</math>. Luego calculamos la mediana según la siguiente fórmula: | ||
| <center><math>M_e=L_i+\cfrac{\frac{N}{2}-F_{i-1}}{F_i-F_{i-1}}\cdot A_i</math></center> | <center><math>M_e=L_i+\cfrac{\frac{N}{2}-F_{i-1}}{F_i-F_{i-1}}\cdot A_i</math></center> | ||
| - | donde: | + | :donde: |
| - | *<math>F_i\;</math> es la frecuencia acumulada del intervalo donde se encuentra la mediana y <math>F_{i-1}\;</math> la frecuencia acumulada del intervalo anterior. Se cumple que <math>F_{i-1} < \cfrac{N}{2} \le F_i</math>. | + | :*<math>F_i\;</math> es la frecuencia acumulada del intervalo donde se encuentra la mediana y <math>F_{i-1}\;</math> la frecuencia acumulada del intervalo anterior. Se cumple que <math>F_{i-1} < \cfrac{N}{2} \le F_i</math>. |
| - | *<math>L_i\;</math> es el límite inferior del intervalo donde se halla la mediana. | + | :*<math>L_i\;</math> es el límite inferior del intervalo donde se halla la mediana. |
| - | *<math>A_i\;</math> es la amplitud del intervalo donde se halla la mediana. | + | :*<math>A_i\;</math> es la amplitud del intervalo donde se halla la mediana. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Mediana|enunciado= | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=15´23" | ||
| + | |url1=https://www.youtube.com/watch?v=O47jC4CaFmk&list=PL5AED12B3B3AA32D3&index=5 | ||
| + | |sinopsis=Mediana correspondiente a una muestra: | ||
| + | *Definición. | ||
| + | *Ejemplos. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_tutomate | ||
| + | |titulo1=Ejemplo 1 (datos no agrupados) | ||
| + | |duracion=4'48" | ||
| + | |sinopsis=Cálculo de la mediana para datos no agrupados. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=rxT_H4kCOYg | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 2 (datos no agrupados) | ||
| + | |duracion=6'09" | ||
| + | |sinopsis=Cálculo de la mediana para datos no agrupados. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=HbmLegjg1Mo | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 3 (datos agrupados) | ||
| + | |duracion=14'24" | ||
| + | |sinopsis=Cálculo de la mediana para datos agrupados sin intervalos. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=l6vWFidMeRQ&t=178s | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 4 (datos en intervalos) | ||
| + | |duracion=7'59" | ||
| + | |sinopsis=Cálculo de la mediana para datos agrupados en intervalos. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=6w022HNDyCk | ||
| + | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Mediana|enunciado= | ||
| + | |||
| + | '''Datos no agrupados:''' | ||
| + | |||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Mediana (datos no agrupados) | + | |titulo1=Actividad 1 |
| - | |descripcion=Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística. | + | |descripcion=Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística con los datos no agrupados. |
| |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta7.htm | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta7.htm | ||
| }} | }} | ||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Autoevaluación: ''Mediana (datos no agrupados)'' | + | |titulo1=Autoevaluación 1 |
| |descripcion=Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística. | |descripcion=Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística. | ||
| |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta7_aut.htm | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta7_aut.htm | ||
| }} | }} | ||
| + | {{AI_vitutor | ||
| + | |descripcion=Ejercicios de autoevaluación sobre la mediana. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/a_9_e.html | ||
| + | |titulo1=Autoevaluación 2 | ||
| + | }} | ||
| + | ---- | ||
| + | '''Datos agrupados puntualmente:''' | ||
| + | |||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Mediana (datos agrupados puntualmente) | + | |titulo1=Actividad 1 |
| |descripcion=Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística con muchos datos en tabla de frecuencias. | |descripcion=Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística con muchos datos en tabla de frecuencias. | ||
| Línea 183: | Línea 284: | ||
| }} | }} | ||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Autoevaluación: ''Mediana (datos agrupados puntualmente)'' | + | |titulo1=Actividad 2 |
| - | |descripcion=Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística con muchos datos en tabla de frecuencias. | + | |
| - | + | ||
| - | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta8_aut.htm | + | |
| - | }} | + | |
| - | {{AI_descartes | + | |
| - | |titulo1=Actividad: ''Mediana'' | + | |
| |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/mediana_discreta_est.htm | |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/mediana_discreta_est.htm | ||
| |descripcion=Calcula en tu cuaderno la mediana para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | |descripcion=Calcula en tu cuaderno la mediana para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | ||
| Línea 207: | Línea 302: | ||
| #¿Cuál es el valor menor que puede tomar? ¿Y el mayor? | #¿Cuál es el valor menor que puede tomar? ¿Y el mayor? | ||
| }} | }} | ||
| - | {{p}} | + | {{AI_descartes |
| - | {{Videotutoriales|titulo=Mediana|enunciado= | + | |titulo1=Autoevaluación |
| - | {{Video_enlace_fonemato | + | |descripcion=Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística con muchos datos en tabla de frecuencias. |
| - | |titulo1=Tutorial | + | |
| - | |duracion=15´23" | + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta8_aut.htm |
| - | |url1=https://www.youtube.com/watch?v=O47jC4CaFmk&list=PL5AED12B3B3AA32D3&index=5 | + | |
| - | |sinopsis=Mediana correspondiente a una muestra: | + | |
| - | *Definición. | + | |
| - | *Ejemplos. | + | |
| }} | }} | ||
| ---- | ---- | ||
| - | {{Video_enlace_tutomate | + | '''Datos agrupados puntualmente o por intervalos:''' |
| - | |titulo1=Ejemplo 1 (datos no agrupados) | + | |
| - | |duracion=4'48" | + | {{AI_cidead |
| - | |sinopsis=Cálculo de la mediana para datos no agrupados. Ejemplos. | + | |titulo1=Actividad |
| - | |url1=https://www.youtube.com/watch?v=rxT_H4kCOYg | + | |descripcion=Actividades en la que podrás aprender a calcular la mediana y los cuartiles primero y tercero de una distribución estadística discreta (con datos agrupados puntualmente) o continua (datos agrupados por intervalos). |
| + | |||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_3c.htm | ||
| }} | }} | ||
| - | {{Video_enlace_abel | ||
| - | |titulo1=Ejemplo 2 (datos no agrupados) | ||
| - | |duracion=6'09" | ||
| - | |sinopsis=Cálculo de la mediana para datos no agrupados. Ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=HbmLegjg1Mo | ||
| }} | }} | ||
| - | {{Video_enlace_abel | + | {{Web_enlace_vitutor |
| - | |titulo1=Ejemplo 3 (datos agrupados) | + | |descripcion=La mediana. Ejemplos. |
| - | |duracion=14'24" | + | |enlace=[http://www.vitutor.com/estadistica/descriptiva/a_9.html Mediana] |
| - | |sinopsis=Cálculo de la mediana para datos agrupados sin intervalos. Ejemplos. | + | |
| - | |url1=https://www.youtube.com/watch?v=l6vWFidMeRQ&t=178s | + | |
| - | }} | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Ejemplo 4 (datos en intervalos) | + | |
| - | |duracion=7'59" | + | |
| - | |sinopsis=Cálculo de la mediana para datos agrupados en intervalos. Ejemplos. | + | |
| - | |url1=https://www.youtube.com/watch?v=6w022HNDyCk | + | |
| }} | }} | ||
| + | {{Ejercicios_vitutor | ||
| + | |descripcion=Ejercicios resueltos sobre la mediana. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/d_5.html | ||
| + | |titulo1=Mediana | ||
| }} | }} | ||
| + | |||
| {{p}} | {{p}} | ||
| Línea 295: | Línea 380: | ||
| ===Desviación media=== | ===Desviación media=== | ||
| {{Desviación media}} | {{Desviación media}} | ||
| - | {{p}} | + | {{Web_enlace_vitutor |
| + | |descripcion=Desviación media. Ejemplos. | ||
| + | |enlace=[http://www.vitutor.com/estadistica/descriptiva/a_14.html Desviación media] | ||
| + | }} | ||
| + | {{Ejercicios_vitutor | ||
| + | |descripcion=Ejercicios resueltos sobre la desviación media. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/d_10.html | ||
| + | |titulo1=Desviación media | ||
| + | }} | ||
| - | ===Varianza y desviación típica=== | + | ===Varianza=== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Se define la '''varianza''' como la media aritmética de los cuadrados de las desviaciones respecto de la media. Es decir: | Se define la '''varianza''' como la media aritmética de los cuadrados de las desviaciones respecto de la media. Es decir: | ||
| Línea 308: | Línea 401: | ||
| <math> \sigma^2\ </math> = <math>{\sum_{i=1}^N x_i^2.f_i \over N} - \bar x^2 </math> | <math> \sigma^2\ </math> = <math>{\sum_{i=1}^N x_i^2.f_i \over N} - \bar x^2 </math> | ||
| </center> | </center> | ||
| - | Se define la '''desviación típica''' como la raíz cuadrada positiva de la varianza. | ||
| - | Si la variable es continua, el cálculo se hace de la misma forma pero utilizando como <math> x_i</math> '''las marcas de clase''': los valores centrales de cada intervalo o la media aritmética de los extremos de cada intervalo. | + | Si agrupamos los datos en intervalos, el cálculo se hace de la misma forma pero utilizando como <math> x_i\;</math> '''las marcas de clase''' (valores centrales de cada intervalo que se calculan haciendo la media aritmética de los extremos de cada intervalo).}} |
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Varianza|enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1a | ||
| + | |duracion=12'20" | ||
| + | |sinopsis=Varianza. Ejemplos. | ||
| + | |url1=https://youtu.be/LLsIf03y8Dg?list=PLwCiNw1sXMSAlIXEx-gl6ZNOx6h_5OrEm | ||
| }} | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1b | ||
| + | |duracion=6'23" | ||
| + | |sinopsis=Otra fórmula para la varianza. | ||
| + | |url1=https://youtu.be/OfHqdAiftlY?list=PLwCiNw1sXMSAlIXEx-gl6ZNOx6h_5OrEm | ||
| + | }} | ||
| + | }} | ||
| + | {{Web_enlace_vitutor | ||
| + | |descripcion=Varianza. Ejemplos. | ||
| + | |enlace=[http://www.vitutor.com/estadistica/descriptiva/a_15.html Varianza] | ||
| + | }} | ||
| + | {{Ejercicios_vitutor | ||
| + | |descripcion=Ejercicios resueltos sobre la varianza. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/d_11.html | ||
| + | |titulo1=Varianza | ||
| + | }} | ||
| + | {{AI_vitutor | ||
| + | |descripcion=Ejercicios de autoevaluación sobre la varianza. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/a_15_e.html | ||
| + | |titulo1=Varianza | ||
| + | }} | ||
| + | |||
| + | ===Desviación típica=== | ||
| + | La varianza no viene expresada en las mismas unidades que los datos, ya que las desviaciones están elevadas al cuadrado. Para evitar esto se define la desviación típica. | ||
| {{p}} | {{p}} | ||
| + | {{Caja_Amarilla|texto= | ||
| + | Se define la '''desviación típica''' como la raíz cuadrada positiva de la varianza: | ||
| + | |||
| + | <center><math> \sigma =\sqrt{{\sum_{i=1}^N x_i^2.f_i \over N} - \bar x^2 } </math> | ||
| + | </center> | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | Cuanto más pequeña sea la desviación típica mayor será la concentración de datos alrededor de la media. | ||
| + | {{p}} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Desviación típica | ||
| + | |duracion=6'23" | ||
| + | |sinopsis=Desviación típica. Ejemplos. | ||
| + | |url1=https://youtu.be/OfHqdAiftlY?list=PLwCiNw1sXMSAlIXEx-gl6ZNOx6h_5OrEm | ||
| + | }} | ||
| + | {{Web_enlace_vitutor | ||
| + | |descripcion=Desviación típica. Ejemplos. | ||
| + | |enlace=[http://www.vitutor.com/estadistica/descriptiva/a_16.html Desviación típica] | ||
| + | }} | ||
| + | {{Ejercicios_vitutor | ||
| + | |descripcion=Ejercicios resueltos sobre la desviación típica. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/d_12.html | ||
| + | |titulo1=Desviación típica | ||
| + | }} | ||
| + | {{AI_vitutor | ||
| + | |descripcion=Ejercicios de autoevaluación sobre la desviación típica. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/a_16_e.html | ||
| + | |titulo1=Desviación típica | ||
| + | }} | ||
| + | |||
| + | ===Actividades y videotutoriales=== | ||
| + | {{Videotutoriales|titulo=Vararianza y desviación típica|enunciado= | ||
| + | {{Video_enlace_tutomate | ||
| + | |titulo1=Tutorial 1a (caso variable discreta) | ||
| + | |duracion=5'37" | ||
| + | |sinopsis=Cálculo de la vararianza y de la desviación típica. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=O5O6CqU0ydU | ||
| + | }} | ||
| + | {{Video_enlace_tutomate | ||
| + | |titulo1=Tutorial 1b (caso variable continua) | ||
| + | |duracion=4'51" | ||
| + | |sinopsis=Cálculo de la vararianza y de la desviación típica. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=1UTRPUNKPrY | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Tutorial 2a | ||
| + | |duracion=27'05" | ||
| + | |sinopsis=Varianza y Desviación Estándar - Introducción y Ejercicio 1 | ||
| + | |url1=https://youtu.be/VTTqr5cAzvw | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Tutorial 2b | ||
| + | |duracion=16'50" | ||
| + | |sinopsis=Varianza y Desviación Estándar de Datos Agrupados de Variable Discreta | ||
| + | |url1=https://youtu.be/7zjzjbxGFQY | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Tutorial 2c | ||
| + | |duracion=21'30" | ||
| + | |sinopsis=Varianza y Desviación Estándar para Datos Agrupados por Intervalos - Ejercicio 1 | ||
| + | |url1=https://youtu.be/gxqORJj_OKk | ||
| + | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Varianza y desviación típica|enunciado= | ||
| {{AI_cidead | {{AI_cidead | ||
| - | |titulo1=Varianza y desviación típica | + | |titulo1=Actividad 1 |
| - | |descripcion=Actividades en la que podrás aprender a calcular la deviación típica y la varianza de una distribución estadística. | + | |descripcion=Actividades en la que podrás aprender a calcular la deviación típica y la varianza de una distribución estadística con datos agrupados puntualmente o por intervalos. |
| |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_4b.htm | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_4b.htm | ||
| }} | }} | ||
| + | |||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Varianza y desviación típica | + | |titulo1=Actividad 2 |
| - | |descripcion=Ejemplos con los que podrás aprender a calcular la deviación típica y la varianza de una distribución estadística. | + | |descripcion=Ejemplos con los que podrás aprender a calcular la deviación típica y la varianza de una distribución estadística con datos agrupados puntualmente o por intervalos. |
| |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta12.htm | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta12.htm | ||
| }} | }} | ||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Autoevaluación: ''Varianza y desviación típica'' | + | |titulo1=Actividad 3 (datos agrupados puntualmente) |
| - | |descripcion=Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la deviación típica y la varianza de una distribución estadística. | + | |
| - | + | ||
| - | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta12_aut.htm | + | |
| - | }} | + | |
| - | + | ||
| - | {{AI_descartes | + | |
| - | |titulo1=Actividad 1: ''''Varianza y desviación típica (Variable discreta)'' | + | |
| |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/varianza_est.htm | |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/varianza_est.htm | ||
| |descripcion=Calcula en tu cuaderno la varianza y desviación típica para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | |descripcion=Calcula en tu cuaderno la varianza y desviación típica para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | ||
| Línea 353: | Línea 535: | ||
| }} | }} | ||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Actividad 2: ''''Varianza y desviación típica (Variable continua)'' | + | |titulo1=Actividad 4 (datos agrupados en intervalos) |
| |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/varianza_est.htm | |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/varianza_est.htm | ||
| |descripcion=Calcula en tu cuaderno el la varianza y desviación típica para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos. Una vez que lo tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | |descripcion=Calcula en tu cuaderno el la varianza y desviación típica para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos. Una vez que lo tengas en tu cuaderno, calcúlala con la escena y compara los resultados. | ||
| Línea 372: | Línea 554: | ||
| #¿Cómo hay que modificar las frecuencias para que aumente la desviación típica?¿Y para que disminuya? | #¿Cómo hay que modificar las frecuencias para que aumente la desviación típica?¿Y para que disminuya? | ||
| }} | }} | ||
| - | {{p}} | + | {{AI_descartes |
| - | {{Videotutoriales|titulo=Vararianza y desviación típica|enunciado= | + | |titulo1=Autoevaluación |
| - | {{Video_enlace_tutomate | + | |descripcion=Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la deviación típica y la varianza de una distribución estadística con datos agrupados puntualmente o por intervalos. |
| - | |titulo1=Tutorial (caso variable discreta) | + | |
| - | |duracion=5'37" | + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/estadistica_1_ciclo/esta12_aut.htm |
| - | |sinopsis=Cálculo de la vararianza y de la desviación típica. Ejemplos. | + | |
| - | |url1=https://www.youtube.com/watch?v=O5O6CqU0ydU | + | |
| - | }} | + | |
| - | {{Video_enlace_tutomate | + | |
| - | |titulo1=Tutorial (caso variable continua) | + | |
| - | |duracion=4'51" | + | |
| - | |sinopsis=Cálculo de la vararianza y de la desviación típica. Ejemplos. | + | |
| - | |url1=https://www.youtube.com/watch?v=1UTRPUNKPrY | + | |
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Actividades=== | ||
| {{Videotutoriales|titulo=Parámetros de dispersión|enunciado= | {{Videotutoriales|titulo=Parámetros de dispersión|enunciado= | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| Línea 439: | Línea 612: | ||
| {{p}} | {{p}} | ||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Actividad: ''Interpretación conjunta de la media y la desviación típica'' | + | |titulo1=Interpretación conjunta de la media y la desviación típica |
| |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/significado_est.htm | |url1=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/significado_est.htm | ||
| - | |descripcion=Representa, en la escena, el diagrama de barras para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. | + | |descripcion=Calcula en tu cuaderno la media y la desviación típica para la siguiente distribución del número de hermanos: |
| + | |||
| + | <center>2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2</center> | ||
| + | |||
| + | Comprueba los resultados obtenidos en la siguiente escena. | ||
| <center><iframe> | <center><iframe> | ||
| Línea 461: | Línea 638: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Caja_Amarilla|texto='''Coeficiente de variación'''. Si hemos realizado un estudio estadístico en dos poblaciones diferentes, y queremos comparar resultados, no podemos acudir a la desviación típica para ver la mayor o menor homogeneidad de los datos, sino a otro parámetro nuevo, llamado coeficiente de variación y que se define como el cociente entre la desviación típica y la media. | + | ===Coeficiente de variación=== |
| + | Si hemos realizado un estudio estadístico en dos poblaciones diferentes, y queremos comparar resultados, no podemos acudir a la desviación típica para ver la mayor o menor homogeneidad de los datos, sino a otro parámetro nuevo, llamado coeficiente de variación. | ||
| + | {{p}} | ||
| + | {{Caja_Amarilla|texto=El '''coeficiente de variación''' se define como el cociente entre la desviación típica y la media. | ||
| + | |||
| + | {{caja|contenido=<math> {CV}={\sigma \over \bar x} </math>}} | ||
| + | |||
| + | El coeficiente de variación se suele expresar en forma de porcentaje: | ||
| + | |||
| <center> | <center> | ||
| - | <math> {CV}={\sigma \over \bar x} </math> | + | <math> {CV}={\sigma \over \bar x} \cdot 100 \ %</math> |
| </center> | </center> | ||
| }} | }} | ||
| + | {{p}} | ||
| + | A una mayor dispersión de los datos le corresponderá un valor del coeficiente de variación mayor. | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplo:|contenido= | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| Línea 472: | Línea 659: | ||
| '''Solución:''' | '''Solución:''' | ||
| - | Un razonamiento falso sería decir que el conjunto de perros es más homogéneo porque su desviación típica es más pequeña, pero si calculamos el coeficiente de variación para ambos: | + | Un razonamiento falso sería decir que el conjunto de perros es más homogéneo porque su desviación típica es más pequeña, ya que si calculamos el coeficiente de variación para ambos: |
| <center> | <center> | ||
| - | <math> {CVv}={50 \over 500}= 0.1 </math> ; <math> {CVp}={10 \over 40}= 0.25 </math> | + | <math> {CV_v}={50 \over 500}= 0.1 \rightarrow 10% </math> {{b}} ; {{b}} <math> {CV_p}={10 \over 40}= 0.25 \rightarrow 25% </math> |
| </center> | </center> | ||
| - | Por tanto, es más homogéneo el conjunto de las vacas. | + | Por tanto, es más disperso el conjunto de los perros y más homogéneo el de las vacas. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Coeficiente de variación | ||
| + | |duracion=4'35" | ||
| + | |sinopsis=Coeficiente de variación. Ejemplos. | ||
| + | |url1=https://youtu.be/44pL-wcwGCI?list=PLwCiNw1sXMSAlIXEx-gl6ZNOx6h_5OrEm | ||
| + | }} | ||
| {{AI_cidead | {{AI_cidead | ||
| |titulo1=Coeficiente de variación | |titulo1=Coeficiente de variación | ||
| Línea 485: | Línea 678: | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_4c.htm | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_4c.htm | ||
| + | }} | ||
| + | {{Web_enlace_vitutor | ||
| + | |descripcion=Coeficiente de variación. Ejemplos. | ||
| + | |enlace=[http://www.vitutor.com/estadistica/descriptiva/a_17.html Coeficiente de variación] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Ejercicios== | + | ==Ejercicios y videotutoriales== |
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Ejercicio 1 | + | |titulo1=Tutorial 1 ''(Parámetros de dispersión)'' |
| |duracion=22'07" | |duracion=22'07" | ||
| |sinopsis=Tutorial que explica, por medio de un sencillo ejercicio, los parámetros de dispersión: rango, desviación media, desviación típica o estándar y el coeficiente de variación. | |sinopsis=Tutorial que explica, por medio de un sencillo ejercicio, los parámetros de dispersión: rango, desviación media, desviación típica o estándar y el coeficiente de variación. | ||
| Línea 497: | Línea 694: | ||
| }} | }} | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Ejercicio 2 | + | |titulo1=Tutorial 2 ''(Parámetros de centralización y de dispersión)'' |
| |duracion=19'09" | |duracion=19'09" | ||
| |sinopsis=Tutorial que explica los parámetros de centralización (moda, mediana, media) y de dispersión (rango, desviación media, desviación típica, coeficiente de variación), mediante un sencillo ejercicio de los personajes de los Simpson. | |sinopsis=Tutorial que explica los parámetros de centralización (moda, mediana, media) y de dispersión (rango, desviación media, desviación típica, coeficiente de variación), mediante un sencillo ejercicio de los personajes de los Simpson. | ||
| Línea 503: | Línea 700: | ||
| |url1=https://www.youtube.com/watch?v=BXu-B1EVYws&index=5&list=PLZNmE9BEzVIkNwELXJr8yFcGGWS5Y0I9i | |url1=https://www.youtube.com/watch?v=BXu-B1EVYws&index=5&list=PLZNmE9BEzVIkNwELXJr8yFcGGWS5Y0I9i | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=13'39" | ||
| + | |sinopsis=Ejercicio de cálculo de los parámetros de centralización y dispersión con datos discretos. | ||
| + | |url1=https://youtu.be/Mywx4zTP77g?list=PLwCiNw1sXMSAlIXEx-gl6ZNOx6h_5OrEm | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=12'14" | ||
| + | |sinopsis=Ejercicio de cálculo de los parámetros de centralización con datos agrupados por intervalos | ||
| + | |url1=https://youtu.be/b4ZHjpU98E8?list=PLwCiNw1sXMSAlIXEx-gl6ZNOx6h_5OrEm | ||
| }} | }} | ||
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
| Línea 509: | Línea 718: | ||
| |sinopsis=Ejercicio de cálculo de los parámetros de centralización y dispersión. | |sinopsis=Ejercicio de cálculo de los parámetros de centralización y dispersión. | ||
| |url1=http://www.unicoos.com/video/matematicas/2-eso/estadistica/parametros-estadisticos/estadistica-01 | |url1=http://www.unicoos.com/video/matematicas/2-eso/estadistica/parametros-estadisticos/estadistica-01 | ||
| + | }} | ||
| + | ---- | ||
| + | {{Web_enlace | ||
| + | |descripcion=En esta página web de "Portal Educativo" podrás encontrar ejemplos de cómo se halla la media, la moda y la mediana para el caso de datos no agrupados o agrupados puntualmente. | ||
| + | |enlace=[http://www.portaleducativo.net/octavo-basico/790/Media-moda-mediana-rango Ejemplos 1 ''(Media, moda, mediana y rango para datos no agrupados o agrupados puntualmente)''] | ||
| + | }} | ||
| + | {{Web_enlace | ||
| + | |descripcion=En esta página web de "Portal Educativo" podrás encontrar ejemplos de cómo se halla la media, la moda y la mediana para el caso de datos no agrupados o agrupados puntualmente. | ||
| + | |enlace=[http://www.portaleducativo.net/octavo-basico/792/Media-moda-y-mediana-para-datos-agrupados Ejemplos 2 ''(Media, moda y mediana para datos agrupados en intervalos)''] | ||
| + | }} | ||
| + | {{AI_vitutor | ||
| + | |descripcion=Ejercicio de autoevaluación sobre el cálculo de los parámetros de centralización y dispersión. | ||
| + | |url1=http://www.vitutor.com/estadistica/descriptiva/a_16_e_1.html | ||
| + | |titulo1=Autoevaluación: ''Parámetros de centralización y de dispersión'' | ||
| }} | }} | ||
Revisión actual
Tabla de contenidos |
Parámetros estadísticos
Después de haber representado los datos gráficamente, ahora llega el momento de hacer un estudio de los mismos. Existen una serie de datos que llamaremos parámetros estadísticos que nos sirven para representar a toda la población o que nos dan a información útil sobre la misma.
Parámetros estadísticos: Son datos que resumen el estudio realizado en la población. Pueden ser de dos tipos:
- Parámetros de centralización. Son datos que representan de forma global a toda la población. Entre ellos tenemos la media aritmética, la moda y la mediana.
- Parámetros de dispersión. Son datos que informan de la concentración o dispersión de los datos respecto de los parámetros de centralización. Entre ellos están el recorrido, la desviación media, la varianza y la desviación típica.
Parámetros de centralización
Moda
- Se define la moda como el valor de la variable que más se repite, es el decir, aquél que tiene mayor frecuencia absoluta. Se representa por Mo.
- Si hay dos o varias puntuaciones con la misma frecuencia máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas.
Actividades en la que podrás aprender a calcular la moda de una distribución estadística.
Actividades en la que podrás aprender a calcular la moda de una distribución estadística.
Ejemplos con los que podrás aprender a calcular la moda de una distribución estadística.
Calcula en tu cuaderno la moda para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
a) Modifica las frecuencias y observa como puede variar el valor de la moda.
b) ¿Puede una distribución estadística tener más de una moda? ¿Pueden ser todos los valores de la variable?
Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la moda de una distribución estadística.
Ejercicios de autoevaluación sobre el cálculo de la moda.
Cálculo de la moda con datos agrupados en intervalos
Llamemos intervalo modal al que tiene mayor frecuencia absoluta y consideremos dos casos:
- Si todos los intervalos tienen la misma amplitud, entonces la moda viene dada por la siguiente fórmula:
|
|
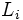 : Extremo inferior del intervalo modal :
: Extremo inferior del intervalo modal :
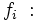 Frecuencia absoluta del intervalo modal.
Frecuencia absoluta del intervalo modal.
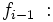 Frecuencia absoluta del intervalo anterior al modal.
Frecuencia absoluta del intervalo anterior al modal.
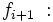 Frecuencia absoluta del intervalo posterior al modal.
Frecuencia absoluta del intervalo posterior al modal.
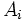 : Amplitud de los intervalos.
: Amplitud de los intervalos.
- Si todos los intervalos no tienen la misma amplitud, entonces la moda viene dada por la siguiente fórmula:
|
|
donde 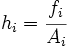 son las alturas de cada intervalo.
son las alturas de cada intervalo.
Moda correspondiente a una muestra:
- Definición.
- Ejemplos.
Cálculo de la moda para datos sin agrupar.
Cálculo de la moda para datos agrupados con o sin intervalos.
La moda. Ejemplos.
Ejercicios resueltos sobre el cálculo de la moda.
Media aritmética
Se define la media aritmética como la suma de todos los datos dividida por el número de datos. Se representa por 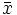 .
.
Cálculo de la media aritmética
- Para datos no agrupados, la media se calcula como sigue:
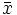 =
= 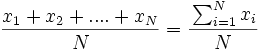
- donde
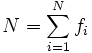 es el número total de datos observados.
es el número total de datos observados.
- Para el caso de datos agrupados puntualmente podemos simplificar el cálculo de la media aritmética con la fórmula:
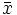 =
= 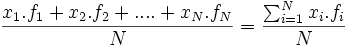
- Para el caso de datos agrupados por intervalos, el cálculo se hace de la misma forma pero utilizando como
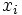 las marcas de clase, que son los valores centrales de cada intervalo (media aritmética de los extremos de cada intervalo).
las marcas de clase, que son los valores centrales de cada intervalo (media aritmética de los extremos de cada intervalo).
Media aritmética correspondiente a una muestra con datos agrupados o no agrupados.
Cálculo de la media para datos no agrupados.
Cálculo de la media para datos agrupados con o sin intervalos.
Actividades en la que podrás aprender a calcular la media aritmética de una distribución estadística.
Ejemplos de cálculo de medias aritméticas de un conjunto de datos no agrupados.
Calcula en tu cuaderno la media para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
- Modifica las frecuencias y observa como puede variar el valor de la media.
- ¿Cuál es el menor valor que puede tomar la media? Justifica la respuesta.
- ¿Cuál es el mayor valor que puede tomar la media? Justifica la respuesta.
Ejemplos de cálculo de medias de un conjunto de muchos datos agrupados o no por intervalos.
Calcula en tu cuaderno la media para el ejemplo de las estaturas: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, agrupando los datos en intervalos. Una vez que lo tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
- Modifica las frecuencias y observa como puede variar el valor de la media.
- ¿Cuál es el menor valor que puede tomar la media? Justifica la respuesta.
- ¿Cuál es el mayor valor que puede tomar la media? Justifica la respuesta.
- En este caso, se ha calculado la media utilizando intervalos, pero como tenemos pocos valores de la variable, calcúlala ahora utilizando la definición, es decir, suma todos las estaturas y divide el resultado por el número de alumnos y alumnas que hay. ¿Coincide el resultado? ¿Por qué?
Actividades para que practiques el cálculo de medias aritméticas de un conjunto de datos no agrupados.
Actividades para que practiques el cálculo de medias de un conjunto de muchos datos agrupados o no por intervalos.
Ejercicios de autoevaluación sobre la media aritmética.
La media aritmética. Ejemplos.
Ejercicios resueltos sobre la media aritmética.
Mediana
Si ordenamos todos los valores de la variable de menor a mayor, se define la mediana como el valor de la variable que está en el centro. Se representa por Me.
Cálculo de la mediana
Para calcular la mediana es necesario que los datos estén ordenados de menor a mayor. Se pueden dar los siguientes casos:
- Datos no agrupados o agrupados puntualmente: Si hay un número impar de datos observados, habrá un sólo valor central, mientras que si hay un número par de datos habrá que hallar la media de los dos valores centrales. En el caso de datos agrupados puntualmente deberemos guiarnos con las frecuencias acumuladas.
- Datos agrupados por intervalos: La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas. Es decir tenemos que buscar el intervalo en el que se encuentre
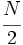 . Luego calculamos la mediana según la siguiente fórmula:
. Luego calculamos la mediana según la siguiente fórmula:
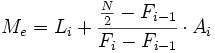
- donde:
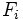 es la frecuencia acumulada del intervalo donde se encuentra la mediana y
es la frecuencia acumulada del intervalo donde se encuentra la mediana y 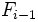 la frecuencia acumulada del intervalo anterior. Se cumple que
la frecuencia acumulada del intervalo anterior. Se cumple que 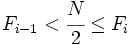 .
.
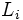 es el límite inferior del intervalo donde se halla la mediana.
es el límite inferior del intervalo donde se halla la mediana.
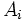 es la amplitud del intervalo donde se halla la mediana.
es la amplitud del intervalo donde se halla la mediana.
Mediana correspondiente a una muestra:
- Definición.
- Ejemplos.
Cálculo de la mediana para datos no agrupados. Ejemplos.
Cálculo de la mediana para datos no agrupados. Ejemplos.
Cálculo de la mediana para datos agrupados sin intervalos. Ejemplos.
Cálculo de la mediana para datos agrupados en intervalos. Ejemplos.
Datos no agrupados:
Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística con los datos no agrupados.
Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística.
Ejercicios de autoevaluación sobre la mediana.
Datos agrupados puntualmente:
Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística con muchos datos en tabla de frecuencias.
Calcula en tu cuaderno la mediana para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
- Modifica las frecuencias y observa como puede variar el valor de la mediana.
- ¿Cuál es el valor menor que puede tomar? ¿Y el mayor?
Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística con muchos datos en tabla de frecuencias.
Datos agrupados puntualmente o por intervalos:
Actividades en la que podrás aprender a calcular la mediana y los cuartiles primero y tercero de una distribución estadística discreta (con datos agrupados puntualmente) o continua (datos agrupados por intervalos).
La mediana. Ejemplos.
Ejercicios resueltos sobre la mediana.
Actividades
Cálculo de la moda y la media para datos agrupados con o sin intervalos.
Cálculo de la media, mediana y moda para datos no agrupados.
Cálculo de la media, mediana y moda para datos agrupados en intervalos.
Parámetros de centralización.
Media aritmética, mediana y moda correspondiente a una muestra de 30 estudiantes en los que se observó el número de horas que pelan la pava diariamente.
Media aritmética, mediana y moda correspondiente a una muestra de 30 estudiantes en los que se observó el número de horas que estudian diariamente.
Parámetros de posición
Los parámetros de posición dividen un conjunto de datos ordenados en grupos con el mismo número de individuos. Hay tres tipos: cuartiles, deciles y percentiles.
Cuartiles
Los cuartiles son los valores de la variable que dividen la serie ordenada de datos en cuatro partes iguales.
- Los cuartiles son tres: Q1, Q2 y Q3, que delimitan al 25%, al 50% y al 75% de los datos, respectivamente.
- Q2 coincide con la mediana.
- La diferencia Q3 - Q1 se llama recorrido intercuartílico.
Cálculo de los cuartiles
Para calcular los cuartiles es necesario que los N datos estén ordenados de menor a mayor.
Procederemos como hacíamos con la mediana, pero ahora buscaremos el lugar que ocupa cada cuartil mediante la expresión

- en lugar del valor que usábamos para la mediana,
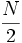 . (Fíjate que para k=2 se obtiene precisamente dicho valor, ya que Q2 es la mediana)
. (Fíjate que para k=2 se obtiene precisamente dicho valor, ya que Q2 es la mediana)
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
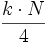 se redondea al siguiente número entero, y el dato ocupe dicho lugar será el cuartil.
se redondea al siguiente número entero, y el dato ocupe dicho lugar será el cuartil.
- Para el caso de datos agrupados en intervalos, la fórmula queda como sigue:
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
|
|
- donde:
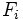 es la frecuencia acumulada del intervalo donde se encuentra el cuartil y
es la frecuencia acumulada del intervalo donde se encuentra el cuartil y 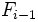 la frecuencia acumulada del intervalo anterior. Se cumple que
la frecuencia acumulada del intervalo anterior. Se cumple que 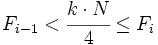 .
.
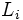 es el límite inferior del intervalo donde se halla el cuartil.
es el límite inferior del intervalo donde se halla el cuartil.
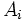 es la amplitud del intervalo donde se halla el cuartil.
es la amplitud del intervalo donde se halla el cuartil.
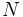 es el número de datos.
es el número de datos.
Actividades en la que podrás aprender a calcular los cuartiles de una distribución estadística.
Cuartiles. Ejemplos.
Ejercicios resueltos sobre cuartiles.
Deciles
Los deciles son los valores de la variable que dividen la serie ordenada de datos en diez partes iguales.
- Los deciles son 9: D1, D2 ... , D9, que delimitan al 10%, al 20%, ..., 90% de los datos, respectivamente.
- D5 coincide con la mediana.
Cálculo de los deciles
Para calcular los deciles es necesario que los N datos estén ordenados de menor a mayor.
Procederemos como antes, pero buscaremos el lugar que ocupa cada decil mediante la expresión
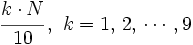
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
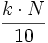 se redondea al siguiente número entero, y el dato que ocupe dicho lugar será el decil.
se redondea al siguiente número entero, y el dato que ocupe dicho lugar será el decil.
- Para el caso de datos agrupados en intervalos, la fórmula queda como sigue:
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
|
|
- donde:
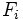 es la frecuencia acumulada del intervalo donde se encuentra el decil y
es la frecuencia acumulada del intervalo donde se encuentra el decil y 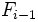 la frecuencia acumulada del intervalo anterior. Se cumple que
la frecuencia acumulada del intervalo anterior. Se cumple que 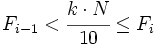 .
.
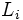 es el límite inferior del intervalo donde se halla el decil.
es el límite inferior del intervalo donde se halla el decil.
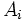 es la amplitud del intervalo donde se halla el decil.
es la amplitud del intervalo donde se halla el decil.
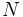 es el número de datos.
es el número de datos.
Deciles. Ejemplos.
Ejercicios resueltos sobre deciles.
Percentiles
Los percentiles son los valores de la variable que dividen la serie ordenada de datos en cien partes iguales.
- Los percentiles son 99: P1, P2 ... , P99, que delimitan al 1%, al 2%, ... , 99% de los datos, respectivamente.
- P50 coincide con la mediana.
Cálculo de los percentiles
Para calcular los percentiles es necesario que los N datos estén ordenados de menor a mayor.
Procederemos como antes, pero buscaremos el lugar que ocupa cada percentil mediante la expresión
|
|
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
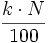 se redondea al siguiente número entero, y el dato que ocupe dicho lugar será el percentil.
se redondea al siguiente número entero, y el dato que ocupe dicho lugar será el percentil.
- Para el caso de datos agrupados en intervalos, la fórmula queda como sigue:
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
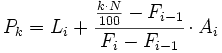
- donde:
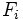 es la frecuencia acumulada del intervalo donde se encuentra el percentil y
es la frecuencia acumulada del intervalo donde se encuentra el percentil y 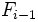 la frecuencia acumulada del intervalo anterior. Se cumple que
la frecuencia acumulada del intervalo anterior. Se cumple que 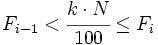 .
.
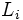 es el límite inferior del intervalo donde se halla el percentil.
es el límite inferior del intervalo donde se halla el percentil.
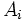 es la amplitud del intervalo donde se halla el percentil.
es la amplitud del intervalo donde se halla el percentil.
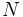 es el número de datos.
es el número de datos.
Percentiles. Ejemplos.
Ejercicios resueltos sobre percentiles.
En esta página web de "Portal Educativo" podrás encontrar ejemplos de cómo se calculan los parámetros de posición.
Cálculo de los cuartiles de una distribución con datos no agrupados.
Cálculo de los cuartiles de una distribución con datos no agrupados.
Cálculo de los deciles de una distribución con datos no agrupados.
Cálculo de los cuartiles de una distribución con datos agrupados puntualmente.
Cálculo de los cuartiles, deciles y percentiles de una distribución con datos agrupados en intervalos.
Cálculo de los cuartiles, deciles y percentiles de una distribución con datos agrupados en intervalos.
Cálculo de los cuartiles y del recorrido intercuartílico de una distribución con datos agrupados en intervalos.
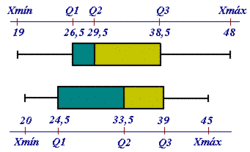
Diagrama de caja y bigotes
En esta página web de "Estadística para todos" podrás encontrar ejemplos de diagramas de cajas y bigotes. Podrás aprender a construirlos y a utilizarlos para comparar distintas distribuciones. Comparar representaciones de datos. |
Parámetros de dispersión
Rango o recorrido
Se define el rango o recorrido como la diferencia entre el mayor y el menor de los valores de la variable. Se representa por R.
Rango o recorrido. Ejemplos.
Rango o recorrido. Ejemplos.
Ejemplos con los que podrás aprender a calcular el rango de una distribución estadística.
Actividades para comprobar lo que has aprendido sobre el cálculo del rango de una distribución estadística.
Desviación media
- La diferencia entre cada dato y la media aritmética del grupo se llaman desviaciones respecto a la media.
- Desviación media de un conjunto de datos es la media aritmética de los valores absolutos de las desviaciones respecto a la media. Nos indica el grado de dispersón (alejamiento) de los datos respecto a su media.
Desviación media. Ejemplos.
Desviación media con más datos. Ejemplos.
Desviaciones respecto a la media. Ejemplos.
Desviación media. Ejemplos.
Ejercicios de autoevaluación sobre el cálculo de la desviación media.
Ejercicios de autoevaluación sobre la desviación media.
Actividades en la que podrás aprender a calcular el rango y la deviación media de una distribución estadística.
Desviación media. Ejemplos.
Ejercicios resueltos sobre la desviación media.
Varianza
Se define la varianza como la media aritmética de los cuadrados de las desviaciones respecto de la media. Es decir:
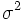 =
= 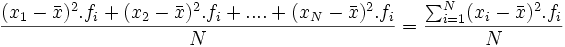
Se calcula más facilmente, con la siguiente fórmula equivalente:
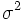 =
= 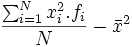
Si agrupamos los datos en intervalos, el cálculo se hace de la misma forma pero utilizando como 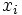 las marcas de clase (valores centrales de cada intervalo que se calculan haciendo la media aritmética de los extremos de cada intervalo).
las marcas de clase (valores centrales de cada intervalo que se calculan haciendo la media aritmética de los extremos de cada intervalo).
Varianza. Ejemplos.
Otra fórmula para la varianza.
Varianza. Ejemplos.
Ejercicios resueltos sobre la varianza.
Ejercicios de autoevaluación sobre la varianza.
Desviación típica
La varianza no viene expresada en las mismas unidades que los datos, ya que las desviaciones están elevadas al cuadrado. Para evitar esto se define la desviación típica.
Se define la desviación típica como la raíz cuadrada positiva de la varianza:
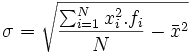
Cuanto más pequeña sea la desviación típica mayor será la concentración de datos alrededor de la media.
Desviación típica. Ejemplos.
Desviación típica. Ejemplos.
Ejercicios resueltos sobre la desviación típica.
Ejercicios de autoevaluación sobre la desviación típica.
Actividades y videotutoriales
Cálculo de la vararianza y de la desviación típica. Ejemplos.
Cálculo de la vararianza y de la desviación típica. Ejemplos.
Varianza y Desviación Estándar - Introducción y Ejercicio 1
Varianza y Desviación Estándar de Datos Agrupados de Variable Discreta
Varianza y Desviación Estándar para Datos Agrupados por Intervalos - Ejercicio 1
Actividades en la que podrás aprender a calcular la deviación típica y la varianza de una distribución estadística con datos agrupados puntualmente o por intervalos.
Ejemplos con los que podrás aprender a calcular la deviación típica y la varianza de una distribución estadística con datos agrupados puntualmente o por intervalos.
Calcula en tu cuaderno la varianza y desviación típica para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
- Modifica las frecuencias y observa como puede variar el valor de la desviación típica.
- ¿Cuál es el menor valor que puede tomar la desviación típica? Intenta construir un caso con desviación típica igual a 0. Justifica la respuesta.
- ¿Cuál es el mayor valor que puede tomar la desviación media? Justifica la respuesta.
- ¿Cómo hay que modificar las frecuencias para que aumente la desviación típica?¿Y para que disminuya?
Calcula en tu cuaderno el la varianza y desviación típica para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos. Una vez que lo tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
- Modifica las frecuencias y observa como puede variar el valor de la desviación típica.
- ¿Cuál es el menor valor que puede tomar la desviación típica? Intenta construir un caso con desviación típica igual a 0. Justifica la respuesta.
- ¿Cuál es el mayor valor que puede tomar la desviación media? Justifica la respuesta.
- ¿Cómo hay que modificar las frecuencias para que aumente la desviación típica?¿Y para que disminuya?
Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la deviación típica y la varianza de una distribución estadística con datos agrupados puntualmente o por intervalos.
Parámetros de dispersión de una muestra:
- Recorrido.
- Varianza.
- Desviación típica.
Determina los parámetros de dispersión de una muestra de 100 estudiantes en los que se observó el número de hermanos.
Determina los parámetros de dispersión de una muestra de 50 piezas en las que se observó el peso de cada una.
Ejercicio sobre una distribución de notas de 20 alumnos. Deberás elaborar una tabla de frecuencias para calcular la media, la varianza, la desviación típica y la desviación media.
Ejercicio sobre una distribución de estaturas de 30 alumnos. Deberás elaborar una tabla de frecuencias para calcular la media, la varianza, la desviación típica y la desviación media.
Interpretación conjunta de la media y la desviación típica
De todas los parámetros estudiados, los más significativos son la media para las medidas de centralización y la desviación típica para las medidas de dispersión.
Vamos a hacer un estudio conjunto de ambas para entender mejor su significado.
La media aritmética es el centro de gravedad de la distribución estadística. Si nos imaginamos el diagrama de barras o el histograma de frecuencias apoyado en un punto del eje horizontal de forma que quedase en equilibrio, el valor de este punto en dicho eje sería el valor de la media.
Como ya hemos comentado, no es suficiente con un parámetro de centralización, es necesario un parámetro de dispersión que nos indique si los datos estudiados están más concentrados o más dispersos. Y este parámetro de dispersión va a ser la desviación típica. Lógicamente si los datos están más concentrados la desviación típica será menor, y si los datos están más dispersos la desviación típica será mayor.
Calcula en tu cuaderno la media y la desviación típica para la siguiente distribución del número de hermanos:
Comprueba los resultados obtenidos en la siguiente escena.
Actividades:
Modifica los valores de las frecuencias, y si quieres introduce más valores de la variable, hasta que el número de datos sea, por ejemplo, N=100. Construye ejemplos con las siguientes características:
- Dale a todas las frecuencias el mismo valor (el que quieras). ¿Cuánto vale la media? ¿Es lógico este resultado? ¿Cuánto vale la desviación típica?
- Ve disminuyendo en varios pasos las frecuencias de los valores centrales y aumentando por igual las frecuencias de los valores extremos, sin que varíe la media ni el número de datos. ¿Qué ocurre con la desviación típica? ¿Por qué sucede esto?
- Realiza ahora el procedimiento inverso, ve aumentando en varios pasos las frecuencias de los valores centrales y disminuyendo por igual las frecuencias de los valores extremos, sin que varíe la media ni el número de datos. ¿Qué ocurre con la desviación típica? ¿Por qué sucede esto?
- ¿Cómo será una variable estadística con desviación típica igual a 0? ¿Compruébalo en la escena?
Coeficiente de variación
Si hemos realizado un estudio estadístico en dos poblaciones diferentes, y queremos comparar resultados, no podemos acudir a la desviación típica para ver la mayor o menor homogeneidad de los datos, sino a otro parámetro nuevo, llamado coeficiente de variación.
El coeficiente de variación se define como el cociente entre la desviación típica y la media.
|
|
El coeficiente de variación se suele expresar en forma de porcentaje:
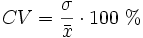
A una mayor dispersión de los datos le corresponderá un valor del coeficiente de variación mayor.
En una exposición de ganado estudiamos un conjunto de vacas con una media de 500 kilos y una desviación típica de 50 kilos. Y observamos también un conjunto de perros con una media de 40 kilos y una desviación típica de 10 kilos. ¿Qué grupo de animales es más homogéneo?
Solución:
Un razonamiento falso sería decir que el conjunto de perros es más homogéneo porque su desviación típica es más pequeña, ya que si calculamos el coeficiente de variación para ambos:
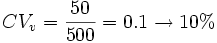 ;
; 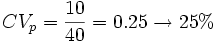
Por tanto, es más disperso el conjunto de los perros y más homogéneo el de las vacas.
Coeficiente de variación. Ejemplos.
Actividades en la que podrás aprender a calcular el coeficiente de variación de una distribución estadística.
Coeficiente de variación. Ejemplos.
Ejercicios y videotutoriales
Tutorial que explica, por medio de un sencillo ejercicio, los parámetros de dispersión: rango, desviación media, desviación típica o estándar y el coeficiente de variación.
Tutorial que explica los parámetros de centralización (moda, mediana, media) y de dispersión (rango, desviación media, desviación típica, coeficiente de variación), mediante un sencillo ejercicio de los personajes de los Simpson. En este ejercicio aparecen pocos en la muestra por lo que se utiliza la definición de cada uno de los parámetros para su cálculo sin necesidad de recurrir a una tabla de frecuencias ni a complejas fórmulas.
Ejercicio de cálculo de los parámetros de centralización y dispersión con datos discretos.
Ejercicio de cálculo de los parámetros de centralización con datos agrupados por intervalos
Ejercicio de cálculo de los parámetros de centralización y dispersión.
En esta página web de "Portal Educativo" podrás encontrar ejemplos de cómo se halla la media, la moda y la mediana para el caso de datos no agrupados o agrupados puntualmente.
En esta página web de "Portal Educativo" podrás encontrar ejemplos de cómo se halla la media, la moda y la mediana para el caso de datos no agrupados o agrupados puntualmente.
Ejercicio de autoevaluación sobre el cálculo de los parámetros de centralización y dispersión.