Plantilla:Def cto num enteros
De Wikipedia
| Revisión de 19:01 9 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Video_enlace_sensei | ||
| - | |titulo1=Los números enteros | ||
| - | |duracion=3'24" | ||
| - | |sinopsis=Los números enteros: utilidad y definición. | ||
| - | |url1=https://www.youtube.com/watch?v=uCLSk-kXsgU | ||
| - | }} | ||
| - | {{p}} | ||
| Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor hay que restarle uno mayor. Nos vemos obligados a ampliar el concepto de [[Sistemas de numeración (1º ESO)#Los números naturales|números naturales]], introduciendo un nuevo conjunto numérico llamado números enteros. | Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor hay que restarle uno mayor. Nos vemos obligados a ampliar el concepto de [[Sistemas de numeración (1º ESO)#Los números naturales|números naturales]], introduciendo un nuevo conjunto numérico llamado números enteros. | ||
| {{p}} | {{p}} | ||
| {{Caja Amarilla|texto=El conjunto de los '''números enteros''' | {{Caja Amarilla|texto=El conjunto de los '''números enteros''' | ||
| {{p}} | {{p}} | ||
| - | <center><math>\mathbb{Z}=\left \lbrace \cdots, -3, -2,-1,\ 0,\ 1 ,\ 2,\ 3, \cdots \right \rbrace</math></center> | + | <center><math>\mathbb{Z}=\left \lbrace -3, -2,-1,\ 0,\ 1 ,\ 2,\ 3, \cdots \right \rbrace</math></center> |
| {{p}} | {{p}} | ||
| Está formado por: | Está formado por: | ||
| - | *El conjunto de los números naturales ('''enteros positivos''' : {{sube|porcentaje=20%|contenido=<math>\mathbb{Z}^+</math>}}) | + | *El conjunto de los números naturales o '''enteros positivos''' : {{sube|porcentaje=20%|contenido=<math>\mathbb{Z}^+=\mathbb{N}=\left \lbrace 1 ,\ 2,\ 3, \cdots \right \rbrace</math>}}. |
| - | *Sus opuestos ('''enteros negativos''': {{sube|porcentaje=20%|contenido=<math>\mathbb{Z}^-</math>}}) | + | *Sus opuestos, los '''enteros negativos''': {{sube|porcentaje=20%|contenido=<math>\mathbb{Z}^-=\left \lbrace \cdots, -1 ,\ -2,\ -3, \cdots \right \rbrace</math>}}. |
| - | *El cero. | + | *El '''cero''' (0). |
| }} | }} | ||
| + | {{p}} | ||
| + | Como consecuencia, <math>\mathbb{N} \subset \mathbb{Z}</math>, que se lee: "''el conjunto de los números naturales está '''incluido''' en el conjunto de los números enteros''". | ||
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Números naturales, números enteros y la recta numérica|enunciado= | {{Videotutoriales|titulo=Números naturales, números enteros y la recta numérica|enunciado= | ||
| - | {{Video_enlace_fonemato | + | {{Video_enlace_sensei |
| |titulo1=Tutorial 1 | |titulo1=Tutorial 1 | ||
| + | |duracion=3'24" | ||
| + | |sinopsis=Los números enteros: utilidad y definición. | ||
| + | |url1=https://www.youtube.com/watch?v=uCLSk-kXsgU | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=3'37" | ||
| + | |sinopsis=Los números enteros: utilidad y definición. | ||
| + | |url1=https://youtu.be/LY8e2Bp6Sig?list=PLwCiNw1sXMSDphdy6B2AIN9Vy7kZrVQbl | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 3a | ||
| + | |duracion=10'19" | ||
| + | |sinopsis=En este video vamos a ver lo que son los números enteros y también las clases de números enteros que hay, es decir, números enteros positivos y números enteros negativos, además del cero. | ||
| + | |url1=https://www.youtube.com/watch?v=hwpS4ShHpvM&list=PLw7Z_p6_h3ozjbs1jLyP5tMZ1bdYbD5TF | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 3b | ||
| + | |duracion=5'03" | ||
| + | |sinopsis=El conjunto de los números enteros. El subconjunto de los números enteros positivos, el de los negativos y el cero. Representación y notación. | ||
| + | |url1=https://www.youtube.com/watch?v=yNDji3A6zTQ&list=PLw7Z_p6_h3oz2MDpS_ZmOBMtFZzoM9IRB | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Tutorial 4 | ||
| + | |duracion=5'48" | ||
| + | |sinopsis=El conjunto de los números enteros. Utilidad. Representación y operaciones en la recta numérica. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=83_tdwzT1Xs | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial 5 | ||
| |duracion=8'58" | |duracion=8'58" | ||
| |sinopsis=Las criaturas o entes llamados números no exixten realmente: nadie ha visto jamás un número, ya sea famoso (como el representado por el símolo 5 y llamado cinco) o no. Los números sólo exixten a la luz de la inteligencia humana. Existen en la medida en que nos son útiles. | |sinopsis=Las criaturas o entes llamados números no exixten realmente: nadie ha visto jamás un número, ya sea famoso (como el representado por el símolo 5 y llamado cinco) o no. Los números sólo exixten a la luz de la inteligencia humana. Existen en la medida en que nos son útiles. | ||
| Línea 28: | Línea 54: | ||
| }} | }} | ||
| {{Video_enlace_mywhyu | {{Video_enlace_mywhyu | ||
| - | |titulo1=Tutorial 2 | + | |titulo1=Tutorial 6 |
| |duracion=10'58" | |duracion=10'58" | ||
| |sinopsis=Number systems evolved from the natural "counting" numbers, to whole numbers (with the addition of zero), to integers (with the addition of negative numbers), and beyond. These number systems are easily understood using the number line. | |sinopsis=Number systems evolved from the natural "counting" numbers, to whole numbers (with the addition of zero), to integers (with the addition of negative numbers), and beyond. These number systems are easily understood using the number line. | ||
| Línea 34: | Línea 60: | ||
| (Disponibles los subtítulos en inglés) | (Disponibles los subtítulos en inglés) | ||
| |url1=https://www.youtube.com/watch?v=8Y82JLMN_Fc&index=4&list=PL7F6C8576EBEDD88F | |url1=https://www.youtube.com/watch?v=8Y82JLMN_Fc&index=4&list=PL7F6C8576EBEDD88F | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Tutorial 7 | ||
| + | |duracion=4'13" | ||
| + | |sinopsis=Utilidad de números negativos en la vida real. El conjunto de los números enteros. Representación en la recta numérica. | ||
| + | |url1=https://youtu.be/dF7zlQrWWsI | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor hay que restarle uno mayor. Nos vemos obligados a ampliar el concepto de números naturales, introduciendo un nuevo conjunto numérico llamado números enteros.
El conjunto de los números enteros
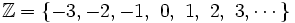
Está formado por:
- El conjunto de los números naturales o enteros positivos :
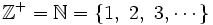 .
.
- Sus opuestos, los enteros negativos:
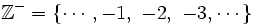 .
.
- El cero (0).
Como consecuencia, 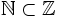 , que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
, que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
Los números enteros: utilidad y definición.
Los números enteros: utilidad y definición.
En este video vamos a ver lo que son los números enteros y también las clases de números enteros que hay, es decir, números enteros positivos y números enteros negativos, además del cero.
El conjunto de los números enteros. El subconjunto de los números enteros positivos, el de los negativos y el cero. Representación y notación.
El conjunto de los números enteros. Utilidad. Representación y operaciones en la recta numérica.
Las criaturas o entes llamados números no exixten realmente: nadie ha visto jamás un número, ya sea famoso (como el representado por el símolo 5 y llamado cinco) o no. Los números sólo exixten a la luz de la inteligencia humana. Existen en la medida en que nos son útiles. Los Números Naturales son todos enteros y positivos. Son muy útiles para contar, pero tienen sus limitaciones, de manera que hubo que inventar otro tipo de números...
Number systems evolved from the natural "counting" numbers, to whole numbers (with the addition of zero), to integers (with the addition of negative numbers), and beyond. These number systems are easily understood using the number line.
(Disponibles los subtítulos en inglés)
Utilidad de números negativos en la vida real. El conjunto de los números enteros. Representación en la recta numérica.

