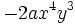Plantilla:Monomios
De Wikipedia
| Revisión de 11:29 22 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Valor numérico de un monomio) |
||
| Línea 10: | Línea 10: | ||
| {{p}} | {{p}} | ||
| {{Nota|titulo=Notación:|texto= | {{Nota|titulo=Notación:|texto= | ||
| - | Para nombrar un monomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del monomio entre paréntesis. | + | Para nombrar un monomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del monomio, entre paréntesis. |
| Por ejemplo: | Por ejemplo: | ||
| Línea 42: | Línea 42: | ||
| {{Video_enlace | {{Video_enlace | ||
| |titulo1=Tutorial 1 | |titulo1=Tutorial 1 | ||
| - | |duracion=3'48" | + | |duracion=2'42" |
| |sinopsis=*Álgebra. | |sinopsis=*Álgebra. | ||
| *Valor numérico de una expresión algebraica. | *Valor numérico de una expresión algebraica. | ||
| Línea 225: | Línea 225: | ||
| {{p}} | {{p}} | ||
| ===Monomios opuestos=== | ===Monomios opuestos=== | ||
| - | {{Caja_Amarilla|texto=Dos monomios se dicen '''opuestos''' si son semejantes y tienen coeficientes opuestos.}} | + | {{Opuesto de un monomio}} |
| - | {{p}} | + | |
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | + | |
| - | Son monomios opuestos: <math>2ax^4y^3\,</math> {{b4}} y {{b4}} <math>-2ax^4y^3\,</math> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace_escuela | + | |
| - | |titulo1=Ejercicio | + | |
| - | |duracion=6'39" | + | |
| - | |sinopsis= | + | |
| - | Calcula el opuesto de los siguientes monomios y luego súmalos: | + | |
| - | + | ||
| - | :33) <math>-2x^3\;</math>; {{b4}} 34) <math>4x^2\;</math>; {{b4}} 35) <math>\cfrac{1}{3}y^2\;</math>; {{b4}} 36) <math>-\cfrac{5}{3}y^5\;</math> | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=DfIoCX93EJw&index=9&list=PLw7Z_p6_h3ow70kSFPZjp_toVtyxYkAaU | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| Línea 251: | Línea 236: | ||
| {{Ejemplo_simple|titulo=Ejemplos:|contenido=Halla el valor numérico de los siguientes monomios: | {{Ejemplo_simple|titulo=Ejemplos:|contenido=Halla el valor numérico de los siguientes monomios: | ||
| - | a) <math>PQ(x)=-2x^2 \;\!</math> para x = 2. | + | a) <math>P(x)=-2x^2 \;\!</math> para x = 2. |
| b) <math>Q(x,y)=3xy \;\!</math> para x = 1 e y = -2. | b) <math>Q(x,y)=3xy \;\!</math> para x = 1 e y = -2. | ||
| Línea 264: | Línea 249: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Valor numérico de un monomio|enunciado= | ||
| + | {{Video_enlace | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=1'24" | ||
| + | |sinopsis=Ejemplo de cálculo del grado y del valor numérico de un monomio con varias variables. | ||
| + | |url1=https://youtu.be/Gpn8gXkSg8I | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_grillo | ||
| + | |titulo1=Ejercicios 1 | ||
| + | |duracion=15'13" | ||
| + | |sinopsis=Ejemplos de cálculo del valor numérico de un monomio. | ||
| + | |url1=https://youtu.be/KCtl5tQ78fk | ||
| + | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| - | |titulo1=Ejercicio | + | |titulo1=Ejercicios 2 |
| |duracion=3'55" | |duracion=3'55" | ||
| |sinopsis= | |sinopsis= | ||
| Línea 277: | Línea 276: | ||
| |url1=https://www.youtube.com/watch?v=iYOWnuXccII&index=7&list=PLw7Z_p6_h3ow70kSFPZjp_toVtyxYkAaU | |url1=https://www.youtube.com/watch?v=iYOWnuXccII&index=7&list=PLw7Z_p6_h3ow70kSFPZjp_toVtyxYkAaU | ||
| + | }} | ||
| }} | }} | ||
Revisión actual
|
Para nombrar un monomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del monomio, entre paréntesis.
Por ejemplo:
a) 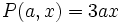 es un monomio de grado 2 y coeficiente 3.
es un monomio de grado 2 y coeficiente 3.
b) 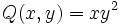 es un monomio de grado 3 y coeficiente 1.
es un monomio de grado 3 y coeficiente 1.
c) 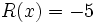 es un monomio de grado 0 y coeficiente -5.
es un monomio de grado 0 y coeficiente -5.
d) 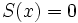 es el monomio nulo. Su grado es 0.
es el monomio nulo. Su grado es 0.
e) En la siguiente escena se puede observar el coeficiente y el grado de un monomio. En la parte superior se pueden cambiar los exponentes de las letras a, b, y x. Para cambiar el coeficiente del monomio modifica la casilla de abajo.
- Álgebra.
- Valor numérico de una expresión algebraica.
- Tipos de expresiones algebraicas.
- Monomios.
- Partes y grado de un monomio.
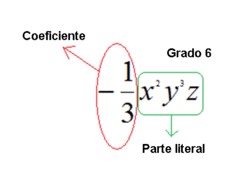
Monomios: Expresión general, coeficiente, parte literal y grado.
Aprende a calcular el grado relativo y absoluto de un monomio.
Nota: Al "grado absoluto" de un monomio se le llama simplemente "grado" del monomio.
Indica el coeficiente, la parte literal y el grado de los siguientes monomios: 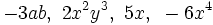
1) Indica cuáles de estas expresiones son monomios:
- a)
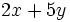 ; b)
; b) 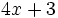 ; c)
; c)  ; d)
; d) 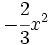 ;
;
- e)
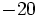 ; f)
; f) 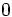 ; g)
; g) 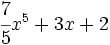
2) Escribe cinco expresiones que sean monomios.
3) Escribe el coeficiente y el grado de cada monomio:
- a)
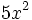 ; b)
; b) 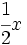 ; c)
; c) 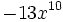 ; d)
; d) 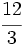 ; e)
; e) 
4) Escribe un monomio de coeficiente -2, otro de coeficiente 7 y otro de coeficiente 1/2.
5) Escribe un monomio de grado 2, otro de grado 1, otro de grado 0 y otro de grado 10.
6) Escribe un monomio de coeficiente -2 y grado 3.
7) Escribe un monomio tal que su coeficiente y su grado sean iguales.
8) Escribe un monomio que no tenga grado y otro que tenga grado cero.
9) Haz una tabla en la que se recojan el coeficiente, la parte literal y el grado de los siguientes monomios:
- a)
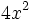 ; b)
; b) 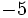 ; c)
; c) 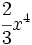 ; d)
; d) 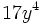 ; e)
; e) 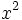
Actividades en la que aprenderás y practicarás a hallar los elementos y el grado de un monomio.
Ejercicios de autoevaluación sobre el grado y los elementos de un monomio.
Monomios semejantes
Son monomios semejantes aquellos que tienen la misma parte literal, es decir, aquellos en los que intervienen las mismas variables con los mismos exponentes.
Son monomios semejantes: 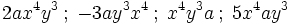
Las letras pueden aparecer en distinto orden ya que por la propiedad conmutativa las podemos reordenar.
Actividades en la que aprenderás y practicarás a hallar los elementos y el grado de un monomio. También practicaras con monomios semejantes y opuestos.
Aprende a distiguir cuando dos monomios son o no semejantes.
Aprende a distiguir cuando dos monomios son o no semejantes.
Aprende a distiguir cuando dos monomios son o no semejantes.
Monomios semejantes. Ejemplos.
Valor numérico de un monomio. Monomios constantes, monomios nulos y monomios semejantes. Ejemplos.
Encuentra los términos semejantes.
10) Indica cuáles de los siguientes monomios son semejantes:
11) Escribe tres monomios semejantes a 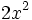 .
.
12) Escribe tres monomios semejantes a 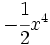 .
.
13) Escribe tres monomios semejantes a 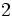 .
.
14) Escribe tres monomios semejantes a 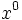 .
.
15) Escribe cinco monomios constantes.
16) Escribe cinco monomios nulos.
Monomios opuestos
Dos monomios se dicen opuestos si son semejantes y tienen coeficientes opuestos.
Calcula el opuesto de los siguientes monomios y luego súmalos:
- 33)
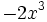 ; 34)
; 34) 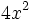 ; 35)
; 35) 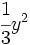 ; 36)
; 36) 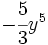
Valor numérico de un monomio
El valor numérico de un monomio es el número que se obtiene al sustituir las letras por ciertos números.
Con la notación que utilizamos para nombrar los monomios y que hemos visto anteriormente, resulta más sencillo hacer referencia al valor numérico de un monomio. El nombre que escogemos está acompañado de las variables del monomio, así que si queremos referirnos a un valor numérico en concreto no tenemos más que escribir el nombre del monomio cambiando las variables por el valor que corresponda. Fíjate cómo se hace en los siguientes ejemplos:
Halla el valor numérico de los siguientes monomios:
a) 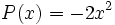 para x = 2.
para x = 2.
b) 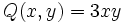 para x = 1 e y = -2.
para x = 1 e y = -2.
Solución:
a) 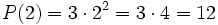
b) 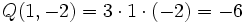
Ejemplo de cálculo del grado y del valor numérico de un monomio con varias variables.
Ejemplos de cálculo del valor numérico de un monomio.
Calcula el valor numérico de los siguientes monomios para los valores de las variables indicados:
- 17)
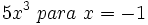
- 18)
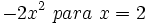
- 19)
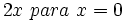
- 20)
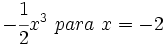
- 21)
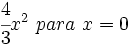
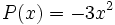
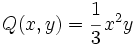
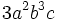
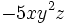
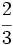
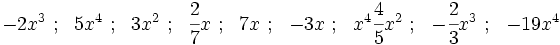
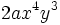 y
y