Plantilla:Concepto de función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:32 2 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja_Amarilla|texto=*Una '''función''' es una relación entre dos variables (por ejemplo, <math>x\;</math> e <math>y\;</math>) que a cada valor de <math>x\;</math> le asigna un '''único''' valor de <math>y\;</math>. | + | {{Definicion de funcion}} |
| - | + | ||
| - | *La variable <math>x\;</math> se llama '''variable independiente''' y la variable <math>y\;</math> se llama '''variable dependiente''', porque su valor depende de <math>x\;</math>. | + | |
| - | + | ||
| - | *Se dice que <math>y\;</math> '''es función''' de <math>x\;</math> y lo representamos por <math>y = f(x)\;\!</math>. También se dice que <math>y\;</math> es la '''imagen''' de <math>x\;</math> mediante la función <math>f\;</math>. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | + | {{p}} |
| - | ''"Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."'' | + | En los siguientes videos se explican los conceptos básicos sobre funciones que trataremos a lo largo de este tema. |
| - | + | {{p}} | |
| - | La relación entre el tiempo (t) que el grifo está abierto y el volumen (V) de agua que hay en el depósito es una función: V=f(t) | + | {{Videotutoriales|titulo=Concepto de función|enunciado= |
| - | + | {{Video_enlace_clasematicas | |
| - | *La '''variable independiente''' (t) es el "tiempo que está abierto el grifo". | + | |titulo1=Tutorial 1 |
| - | *La '''variable dependiente''' (V) es el "volumen de agua que se ha llenado el depósito". | + | |duracion=27'16" |
| + | |url1=https://www.youtube.com/watch?v=sZIcLmsFknM&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3&index=1 | ||
| + | |sinopsis=Tutorial en el que se explican los conceptos básicos sobre funciones: variable independiente, dependiente, imagen, preimagen, dominio, recorrido... necesarios para poder comprender la terminología que se emplea en el análisis matemático. | ||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_matemovil |
| - | ===Dominio e imagen de una función=== | + | |titulo1=Tutorial 2 |
| - | {{Caja_Amarilla|texto= | + | |duracion=46'32" |
| - | *El conjunto de valores de la variable independiente, <math>x\;</math>, para los que hay un valor de la variable dependiente, <math>y\;</math>, se llama '''dominio de definición''' de la función (Se denota <math>Dom_f\;</math>). | + | |sinopsis=*Definición de función. |
| + | *Dominio e imagen (o rango). | ||
| + | *Distintas formas de representar una función. | ||
| + | *Ejercicios resueltos. | ||
| - | *El conjunto de valores que toma la variable independiente, <math>y\;</math>, se llama '''imagen''', '''recorrido''' o '''rango''' de la función (Se denota <math>Im_f\;</math>) | + | |url1=https://youtu.be/onh9C8dv9x4 |
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| - | Consideremos el ejemplo anterior: | ||
| - | |||
| - | ''"Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."'' | ||
| - | |||
| - | :t = "Tiempo que está abierto el grifo". | ||
| - | :V = "Volumen de agua que se ha llenado el depósito". | ||
| - | |||
| - | *'''Dominio:''' El tiempo que el grifo puede estar abierto es un número que varía entre 0 segundos y 100 segundos: <math>Dom_f=[0,100]\;</math> | ||
| - | *'''Recorrido:''' El volumen de agua que se ha llenado el depósito es un número que varía ente 0 litros y 200 litros: <math>Im_f=[0,200]\;</math> | ||
| - | }} | ||
Revisión actual
- Una función es una relación entre dos variables (por ejemplo,
e 
) que a cada valor de le asigna un único valor de .
- La variable se llama variable independiente y la variable se llama variable dependiente, porque su valor depende de .
- Se dice que es función de y lo representamos por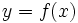
. También se dice que es la imagen de mediante la función 
.
"Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
La relación entre el tiempo (t) que el grifo está abierto y el volumen (V) de agua que hay en el depósito es una función.
El volumen es función del tiempo: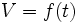 
- La variable independiente (t) es el "tiempo que está abierto el grifo".
- La variable dependiente (V) es el "volumen de agua que se ha llenado el depósito".
En los siguientes videos se explican los conceptos básicos sobre funciones que trataremos a lo largo de este tema.
Tutorial 1 (27'16") Sinopsis:Tutorial en el que se explican los conceptos básicos sobre funciones: variable independiente, dependiente, imagen, preimagen, dominio, recorrido... necesarios para poder comprender la terminología que se emplea en el análisis matemático.
Tutorial 2 (46'32") Sinopsis: - Definición de función.
- Dominio e imagen (o rango).
- Distintas formas de representar una función.
- Ejercicios resueltos.
