Plantilla:Crecimiento y variación de una función

De Wikipedia

(Diferencia entre revisiones)
Revisión de 16:58 3 nov 2016
Coordinador (Discusión | contribuciones)

← Ir a diferencia anterior		 Revisión actual
Coordinador (Discusión | contribuciones)

Línea 1: Línea 1:
{{Caja_Amarilla {{Caja_Amarilla
|texto= |texto=
-*Una función es '''creciente''' en un tramo cuando al aumentar la variable independiente <math>x\;</math> en ese tramo, aumenta la variable dependiente <math>y\;</math>.+*Una función es '''creciente''' en un intervalo I cuando al aumentar la variable independiente <math>x\;</math> en ese intervalo, aumenta la variable dependiente <math>y\;</math>.
- +<center><math>\forall x_1,x_2 \in I, x_1<x_2 \Rightarrow f(x_1)<f(x_2)</math></center>
-*Una función es '''decreciente''' en un tramo cuando al aumentar la variable independiente <math>x\;</math> en ese tramo, disminuye la variable dependiente <math>y\;</math>.+*Una función es '''decreciente''' en un intervalo cuando al aumentar la variable independiente <math>x\;</math> en ese intervalo, disminuye la variable dependiente <math>y\;</math>.
-}}{{p}}+<center><math>\forall x_1,x_2 \in I, x_1<x_2 \Rightarrow f(x_1)>f(x_2)</math></center>
-{{Caja_Amarilla+*Una función es '''constante''' en un intervalo cuando al aumentar la variable independiente <math>x\;</math> en ese intervalo, la variable dependiente <math>y\;</math> no varía, siempre toma un mismo valor <math>k\;</math>.
-|texto= +<center><math>f(x)=k \ , \forall x \in I</math></center>
-Se llama '''variación''' de una función en un intervalo, a lo que varía la variable dependiente de un extremo a otro del intervalo.}}+}}
{{p}} {{p}}
-{{AI2|titulo=Actividad interactiva: ''Crecimiento y variación''+{{Videotutoriales|titulo=Crecimiento de una función|enunciado=
-|cuerpo=+{{Video_enlace
-{{ai_cuerpo+|titulo1=Tutorial 1
-|enunciado=1. Ejemplo de función creciente, decreciente y constante.+|duracion=2'50"
-|actividad=+|url1=https://youtu.be/dcpst_xi8as
-Observa las escenas y mueve el punto P. Vemos que en una la gráfica sube (crecimiento), en otra baja (decrecimiento) y en la última ni sube ni baja, es decir, permanece constante.+|sinopsis=Tutorial en el que se explica el estudio del crecimiento de una función dada su gráfica.
-<center><iframe>+}}
-url=http://maralboran.org/web_ma/descartes/4a_eso/El_lenguaje_de_las_funciones/variacion1_1.html+{{Video_enlace_clasematicas
-width=100%+|titulo1=Tutorial 2
-height=adjust+|duracion=7'10"
-name=myframe+|url1=https://www.youtube.com/watch?v=VRmzX7bAwlQ&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3&index=10
-</iframe></center>+|sinopsis=Tutorial en el que se explica el estudio del crecimiento de una función dada su gráfica.
}} }}
-{{ai_cuerpo 
-|enunciado=2. Estudia el crecimiento y la variación de la siguiente función. 
-|actividad= 
-Observa la escena y mueve el punto P para contestar a las siguientes preguntas: 
-<center><iframe>+{{Video_enlace_abel
-url=http://maralboran.org/web_ma/descartes/4a_eso/El_lenguaje_de_las_funciones/variacion2_1.html+|titulo1=Tutorial 3
-width=500+|duracion=12´24"
-height=adjust+|url1=https://www.youtube.com/watch?v=rKjPXCGgyOQ
-name=myframe+|sinopsis=Conceptos de función creciente, decreciente y constante.
-</iframe></center>+
-a) Indica en qué intervalos la función crece o decrece.<br>+
-b) Indica la variación de la función entre los valores x=-4 y x=0.+
}} }}
 +----
 +{{Video_enlace_childtopia
 +|titulo1=Ejercicio 1
 +|duracion=1'58"
 +|url1=https://www.youtube.com/watch?v=MTaNBjwPyaE&index=1&list=PLD4A6C822A23490D7
 +|sinopsis=Estudio del crecimiento de una función a partir de su gráfica.
}} }}
 +{{Video_enlace_childtopia
 +|titulo1=Ejercicio 2
 +|duracion=2'08"
 +|url1=https://www.youtube.com/watch?v=R-3FgClwCho&index=2&list=PLD4A6C822A23490D7
 +|sinopsis=Estudio del crecimiento de una función a partir de su gráfica.
 +}}
 +{{Video_enlace_childtopia
 +|titulo1=Ejercicio 3
 +|duracion=1'24"
 +|url1=https://www.youtube.com/watch?v=d8-cU1zoGE0&index=3&list=PLD4A6C822A23490D7
 +|sinopsis=Estudio del crecimiento de una función a partir de su gráfica.
 +}}
 +{{Video_enlace_childtopia
 +|titulo1=Ejercicio 4
 +|duracion=1'28"
 +|url1=https://www.youtube.com/watch?v=jPUQV2G0s4g&index=4&list=PLD4A6C822A23490D7
 +|sinopsis=Estudio del crecimiento de una función a partir de su gráfica.
 +}}
 +}}
 +{{p}}
 +{{Actividades|titulo=Crecimiento de una función|enunciado=
 +{{AI_cidead
 +|titulo1=Actividad 1
 +|descripcion=Actividades con las que aprenderás a determinar los intervalos de crecimiento y decrecimiento de una función.
 +|url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena9/3quincena9_contenidos_2d.htm
 +}}
 +{{Geogebra_enlace
 +|descripcion=En esta escena podrás ver cuando una función es creciente, decreciente o constante.
 +|enlace=[http://ggbm.at/FSnFhEwb Actividad 2]
 +}}
 +{{AI_Khan
 +|titulo1=Autoevaluación
 +|descripcion=Determina los intervalos de crecimiento y decrecimiento de una función.
 +|url1=http://es.khanacademy.org/math/algebra/algebra-functions/positive-negative-increasing-decreasing-intervals/e/increasing-decreasing-intervals-of-functions
 +}}
 +}}
 +{{p}}
 +{{Caja_Amarilla
 +|texto=
 +Se llama '''variación''' de una función <math>f\;</math> en un intervalo <math>[a,b]\;</math>, a lo que varía la variable dependiente de un extremo a otro del intervalo:
 +<center><math>\Delta f_{[a,b]}=f(b)-f(a)\;</math></center>
 +}}
 +{{p}}

Revisión actual

  • Una función es creciente en un intervalo I cuando al aumentar la variable independiente x\; en ese intervalo, aumenta la variable dependiente y\;.
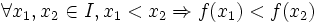
\forall x_1,x_2 \in I, x_1<x_2 \Rightarrow f(x_1)<f(x_2)
  • Una función es decreciente en un intervalo cuando al aumentar la variable independiente x\; en ese intervalo, disminuye la variable dependiente y\;.
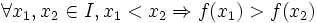
\forall x_1,x_2 \in I, x_1<x_2 \Rightarrow f(x_1)>f(x_2)
  • Una función es constante en un intervalo cuando al aumentar la variable independiente x\; en ese intervalo, la variable dependiente y\; no varía, siempre toma un mismo valor k\;.
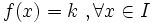
f(x)=k \ , \forall x \in I

video
Crecimiento de una función
Tutorial 1 (2'50")     Sinopsis:

Tutorial en el que se explica el estudio del crecimiento de una función dada su gráfica.

Tutorial 2 (7'10")     Sinopsis:

Tutorial en el que se explica el estudio del crecimiento de una función dada su gráfica.

Tutorial 3 (12´24")     Sinopsis:

Conceptos de función creciente, decreciente y constante.

Ejercicio 1 (1'58")     Sinopsis:

Estudio del crecimiento de una función a partir de su gráfica.

Ejercicio 2 (2'08")     Sinopsis:

Estudio del crecimiento de una función a partir de su gráfica.

Ejercicio 3 (1'24")     Sinopsis:

Estudio del crecimiento de una función a partir de su gráfica.

Ejercicio 4 (1'28")     Sinopsis:

Estudio del crecimiento de una función a partir de su gráfica.

video
Crecimiento de una función
Actividad 1     Descripción:

Actividades con las que aprenderás a determinar los intervalos de crecimiento y decrecimiento de una función.

Actividad 2     Descripción:

En esta escena podrás ver cuando una función es creciente, decreciente o constante.

Autoevaluación     Descripción:

Determina los intervalos de crecimiento y decrecimiento de una función.

Se llama variación de una función f\; en un intervalo [a,b]\;, a lo que varía la variable dependiente de un extremo a otro del intervalo:

\Delta f_{[a,b]}=f(b)-f(a)\;

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Crecimiento_y_variaci%C3%B3n_de_una_funci%C3%B3n"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda