Vídeos de Matemáticas
De Wikipedia
| Revisión de 13:09 10 dic 2007 Coordinador (Discusión | contribuciones) (→MÁS POR MENOS) ← Ir a diferencia anterior |
Revisión de 13:25 10 dic 2007 Coordinador (Discusión | contribuciones) (→MÁS POR MENOS) Ir a siguiente diferencia → |
||
| Línea 171: | Línea 171: | ||
| |url1=http://maralboran.org/web_ma/videos/naturales/naturales.htm | |url1=http://maralboran.org/web_ma/videos/naturales/naturales.htm | ||
| |titulo2=Acceso por red TIC | |titulo2=Acceso por red TIC | ||
| - | |url2= | + | |url2=http://c0/helvia/aula/archivos/repositorio/html/113/index.htm |
| |sinopsis=Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos | |sinopsis=Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos | ||
| números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. | números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. | ||
| Línea 181: | Línea 181: | ||
| |url1=http://maralboran.org/web_ma/videos/fractales/fractales.htm | |url1=http://maralboran.org/web_ma/videos/fractales/fractales.htm | ||
| |titulo2=Acceso por red TIC | |titulo2=Acceso por red TIC | ||
| - | |url2= | + | |url2=http://c0/helvia/aula/archivos/repositorio/html/114/index.htm |
| |sinopsis=El ordenador los ha puesto de moda. Y sin embargo ya eran conocidos a principios de siglo. Nos referimos a los fractales. Son los objetos matemáticos más atractivos, espectaculares y enigmáticos. A medio camino entre la linea y el plano, entre el plano y el espacio, rompen hasta con el concepto clásico de dimensión. Sus dimensiones no son números enteros, de ahí su extraño nombre. Y sin embargo se pueden obtener mediante simples iteracciones, es decir, repitiendo indefinidamente procedimientos geométricos o funcionales muy simples. Han dado origen a una nueva geometría: la geometría fractal. Una nueva herramienta matemática capaz de arrojar un poco de luz sobre los fenómenos caóticos y de mostrarnos que incluso en el caos es posible encontrar un determinado orden. | |sinopsis=El ordenador los ha puesto de moda. Y sin embargo ya eran conocidos a principios de siglo. Nos referimos a los fractales. Son los objetos matemáticos más atractivos, espectaculares y enigmáticos. A medio camino entre la linea y el plano, entre el plano y el espacio, rompen hasta con el concepto clásico de dimensión. Sus dimensiones no son números enteros, de ahí su extraño nombre. Y sin embargo se pueden obtener mediante simples iteracciones, es decir, repitiendo indefinidamente procedimientos geométricos o funcionales muy simples. Han dado origen a una nueva geometría: la geometría fractal. Una nueva herramienta matemática capaz de arrojar un poco de luz sobre los fenómenos caóticos y de mostrarnos que incluso en el caos es posible encontrar un determinado orden. | ||
| }} | }} | ||
| Línea 190: | Línea 190: | ||
| |url1=http://maralboran.org/web_ma/videos/electoral/electoral.htm | |url1=http://maralboran.org/web_ma/videos/electoral/electoral.htm | ||
| |titulo2=Acceso por red TIC | |titulo2=Acceso por red TIC | ||
| - | |url2= | + | |url2=http://c0/helvia/aula/archivos/repositorio/html/115/index.htm |
| |sinopsis=Cuando se anuncian unas elecciones una poderosa máquina matemática se pone en marcha. Es la Estadística a través de las encuestas y sondeos de opinión. Analizaremos en este programa los aspectos matemáticos más destacados de este tipo de sondeos y sus márgenes de fiabilidad. Pero después de depositar el voto las matemáticas siguen actuando. El sistema electoral español está basado en la ley D´Hont un sofisticado mecanismo en el que la aritmética interviene de forma determinante. Estudiaremos las características matemáticas de este sistema y su influencia en el mapa parlamentario en nuestro país. | |sinopsis=Cuando se anuncian unas elecciones una poderosa máquina matemática se pone en marcha. Es la Estadística a través de las encuestas y sondeos de opinión. Analizaremos en este programa los aspectos matemáticos más destacados de este tipo de sondeos y sus márgenes de fiabilidad. Pero después de depositar el voto las matemáticas siguen actuando. El sistema electoral español está basado en la ley D´Hont un sofisticado mecanismo en el que la aritmética interviene de forma determinante. Estudiaremos las características matemáticas de este sistema y su influencia en el mapa parlamentario en nuestro país. | ||
| }} | }} | ||
| Línea 208: | Línea 208: | ||
| |url1=http://maralboran.org/web_ma/videos/graficas/graficas.htm | |url1=http://maralboran.org/web_ma/videos/graficas/graficas.htm | ||
| |titulo2=Acceso por red TIC | |titulo2=Acceso por red TIC | ||
| - | |url2= | + | |url2=http://c0/helvia/aula/archivos/repositorio/html/116/index.htm |
| |sinopsis=Las gráficas de contenido matemático se han convertido en el lenguaje más universal de finales del siglo XX. En cualquier medio de comunicación cada vez que se quiere dar información cuantitativa de un proceso aparece una gráfica matemática. Sus ventajas son incuestionables, son capaces de ofrecer gran cantidad de información de un simple vistazo. Constituyen un instrumento imprescindible en campos tan dispares como la medicina, la economía, la física, la biología y hasta en el deporte. En este programa investigaremos su origen relativamente reciente, tienen poco más de 200 años de existencia, y sus distintas aplicaciones y daremos algunos consejos para interpretar de forma crítica la información presentada en forma de gráficas. | |sinopsis=Las gráficas de contenido matemático se han convertido en el lenguaje más universal de finales del siglo XX. En cualquier medio de comunicación cada vez que se quiere dar información cuantitativa de un proceso aparece una gráfica matemática. Sus ventajas son incuestionables, son capaces de ofrecer gran cantidad de información de un simple vistazo. Constituyen un instrumento imprescindible en campos tan dispares como la medicina, la economía, la física, la biología y hasta en el deporte. En este programa investigaremos su origen relativamente reciente, tienen poco más de 200 años de existencia, y sus distintas aplicaciones y daremos algunos consejos para interpretar de forma crítica la información presentada en forma de gráficas. | ||
| }} | }} | ||
| Línea 217: | Línea 217: | ||
| |url1=http://maralboran.org/web_ma/videos/realidad/realidad.htm | |url1=http://maralboran.org/web_ma/videos/realidad/realidad.htm | ||
| |titulo2=Acceso por red TIC | |titulo2=Acceso por red TIC | ||
| - | |url2= | + | |url2=http://c0/helvia/aula/archivos/repositorio/html/117/index.htm |
| |sinopsis=La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles. | |sinopsis=La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles. | ||
| }} | }} | ||
Revisión de 13:25 10 dic 2007
UNIVERSO MATEMÁTICO
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema. Perolas Matemáticas le deben a Pitágoras y a los pitagóricos mucho más. Ellos son los que pusieron las primeras piedras científicas no solo de la Geometría sino también de la Aritmética, de la Astronomía y de la Música. Pero antes de Pitágoras otras dos culturas habían desarrollado unas matemáticas prácticas muy potentes: los babilonios y los egipcios. Exploraremos sus aportaciones tanto en el terreno de los sistemas de numeración que empleaban, como de sus habilidades astronómicas y geométricas. Del sistema sexagesimal de los babilonios hemos heredado tanto la división de la circunferencia en 360 grados como la forma actual de medir el tiempo en horas, minutos y segundos. Sus tablillas nos reservan unas cuantas sorpresas matemáticas. Quizás la más importante, la tablilla Plimpton, nos desvela el hecho sorprendente de que conocían las ternas pitagóricas mil años antes de que Pitagoras viera la luz.Disfrutaremos de alguna de las demostraciones gráficas más llamativas del famoso teorema, el que cuenta con un mayor número de demostraciones distintas a lo largo de la historia.
Si las matemáticas tienen algún número emblemático ese es "pi" (π = 3,141592...). La figura de Ramanujan, un joven indio sin formación universitaria está intimamente ligada al número pi. A principio de siglo descubrió nuevas series infinitas para obtener valores aproximados de pi. Lasmismas que utilizan los grandes ordenadores para obtener millones de cifras de este familiar y extraño número.Pero el verdadero padre de pi es un matemático griego de hace 2.300 años, Arquímedes. Él descubrió la famosa fórmula del área del círculo. Y también el volumen y el área de la esfera. De paso invento el primer método para obtener valores aproximados de pi aproximando el círculo mediante polígonos de un número creciente de lados.Pero pi no sólo aparece en matemáticas cuando se habla de círculos o esferas, su presencia en relaciones numéricas, en el cálculo de probabilidades y hasta en estudiosestadísticos la confieren una omnipresencia casi mágica.
Con la llegada del euro volverán los céntimos y unos viejos conocidos van a adquirir un protagonismo social que no tenían desde hace mucho tiempo: los números decimales. Unos números que, a pesar de la creencia popular de que existen desde los comienzos de las matemáticas, sólo llevan entre nosotros cuatro siglos. Y es que la historia de los números es más compleja de lo que sospechamos. A lo largo del programa haremos una excursión por el tiempo para descubrir la historia de las cifras. Descubriremos las cifras y la forma de utilizarlas de babilonios, egipcios, griegos y romanos hasta llegar hasta nuestras populares 10 cifras: 1, 2, 3, 4, 5… Pero incluso estas cifras heredadas de los árabes no siempre han sido la herramienta habitula para calcular. Conoceremos las aventuras de estos símbolos desde su nacimiento hasta nuestros días, en que sin duda son los símbolos más universalmente utilizados.
A principios de siglo XVII un abogado, aficionado a las matemáticas va a lanzar una serie de retos, basados en los números más simples, los enteros, a toda la comunidad matemática. Es Pierre de Fermat. La inspiración para estos retos la encontró en un antiguo libro de matemáticas escrito allá por el siglo III, la Aritmética de Diofanto. En uno de sus márgenes Fermat va a escribir una frase que se convertirá en una de las más atractivas de la historia de las matemáticas. Su famoso último teorema:
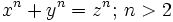 ”
” Fermat afirma que había encontrado la demostración pero por desgracia no le cabe el margen. Una desgracia que ha traído en jaque a los mejores matemáticos durante más de 350 años. Haremos un recorrido histórico por los intentos de demostrar este teorema a lo largo de tres siglos y presentaremos a Wiles, un matemático inglés que en 1994 pasó a la historia… Por fin alguien había conseguido demostrar el “ultimo teorema de Fermat”
Principios del siglo XIX. Un joven matemático acaba de resolver un problema de más de 2.000 años de antigüedad: la construcción con regla y compás del polígono regular de 17 lados. Esta va a ser una de las primeras anotaciones que hará en una vieja libreta de 19 páginas. Al final de su vida las anotaciones no llegarán a 50, pero sin duda esta libreta será el sueño de cualquier matemático del siglo XIX. Las aportaciones que en ella se reflejan contienen el suficiente material para mantener ocupados a todos los matemáticos del siglo.
Sin embargo la fama de este joven, Gauss le va a venir de los cielos. A finales de 1800 los astrónomos descubren un nuevo objeto celeste. No se trata de un cometa, bien podía ser el planeta buscado tantos años entre Marte y Júpiter. Por desgracia se le pierde la pista. Pero con las pocas observaciones realizadas, Gauss se pone a la tarea de deducir su órbita y señala el lugar del cielo hacia donde apuntar los telescopios un año más tarde.
Y en efecto alli aparece Ceres. Las increíbles aportaciones de Gauss no se limitan al mundo de las Matemáticas y de la Astronomía. Junto a Weber va a poner en marcha el primer telégrafo operativo unos años antes que el de Morse. En magnetismo también nos ha dejado su huella: el primer mapa magnético de la Tierra es obra suya. No es inmerecido el título de Príncipe de los Matemáticos, aunque reinó en casi todas las ciencias.
Euler es un matemático entrañable, y no sólo por sus trabajos. A lo largo del siglo XVIII ensanchó las fronteras del conocimiento matemático en todos sus campos. Sus obras completas, Opera Omnia, ocupan más de 87 grandes volúmenes, y la importancia de sus descubrimientos nos hacen dudar a veces que puedan ser obra de una sola persona. Aunque Euler no era una persona normal: era un genio.A los 19 años ganó el premio de la Academia de Ciencias de Francia por un trabajo sobre la mejor ubicación de los mástiles de los barcos. Esto no es sorprendente, salvo por el hecho de que Euler nació en Basilea ( Suiza) y no había visto un barco en su vida. Volvería a ganar otros once premios de la Academia. Euler recogió el guante de todos los retos planteados por Fermat y dio respuesta satisfactoria a todos menos uno, el último teorema. Hoy su nombre está asociado a resultados de casi todas las ramas de las matemáticas: análisis, álgebra, teoría de números, series, geometría, astronomía… Lo más sorprendente es que Euler escribió más de la mitad de su obra completamente ciego realizando sus cálculo mentalmente. Nada extraño para alguien que era capaz de recitar la Eneida completa y en latín.
Sin duda Newton es el autor del primer paso de la carrera espacial. Las Leyes descubiertas por él son las que han permitido al hombre poner un pie en la Luna o enviar naves a Marte y Venus, explorar los planetas exteriores: Júpiter, Saturno, Neptuno y Urano. Su modelo de telescopio ha permitido ver más lejos en cielo. Sin duda los astrónomos le deben mucho a Newton. Pero los matemáticos y de paso el resto de los científicos le deben tanto a más. Él junto a Leibniz, aunque sería mejor decir al mismo tiempo que Leibniz, son los descubridores de la más potente y maravillosa herramienta matemática: el Cálculo. Newton tuvo en vida un prestigio y un reconocimiento social aún mayor que el que pudo tener Einstein en nuestro siglo. Como los reyes y muy pocos nobles fue enterrado en la abadía de Westminster. Leibniz murió sólo y abandonado por todos. A su entierro en Hannover sólo asistió su criado. Hoy los dos comparten por igual la gloria de ser los padres de las dos herramientas más potentes del universo matemático: el cálculo diferencial y el cálculo integral. El instrumento ideal para entender y explicar el funcionamiento del mundo real, desde las cosas más próximas hasta el rincón más alejado del universo.
En 1791, haciendo un alto en sus disputas políticas, la Asamblea Nacional Francesa define lo que con los años se convertirá en la medida de longitud universal: el metro. La diezmillonésima parte del cuadrante del meridiano terrestre. Gracias a los matemáticos franceses hoy compramos en kilos y viajamos kilómetros.Una pléyade de notables matemáticos como nunca antes habían convivido en Francia, va a vivir de forma intensa los acontecimientos de la Revolución Francesa: Joseph Louis Lagrange, Gaspard Monge, Peirre Simon de Laplace, Adrien Marie Legendre, y el marqués de Condorcet, van a llevar a la matemática francesa a su más alta cima. Ellos van a poner los fundamentos científicos del Análisis, del cálculo de probabilidades, de la Geometría descriptiva y de la Astronomía moderna. Pero van a hacer algo más: van a crear el modelo de la moderna enseñanza de las matemáticas superiores, un modelo que pervivirá más de dos siglos. 14 de julio, fiesta nacional francesa. Los franceses celebran el nacimiento del Estado moderno. El resto del mundo deberíamos celebrar con ellos algo quizás más importante: uno de los momentos más brillantes de la Ciencia Moderna.
¿Entienden las Matemáticas de sexos? ¿Son los grandes misterios de las Matemáticas algo exclusivo de los hombres? ¿Por qué, a lo largo de la historia, hay tan pocas mujeres que hayan destacado en una disciplina científica tan antigua? Aunque parece que en la actualidad existe un equilibrio entre el número de chicos y de chicas que estudian matemáticas, esto es un fenómeno relativamente reciente. Desde luego hace cuarenta años esto no ocurría. Para descubrir la presencia de las mujeres en el Universo de las Matemáticas haremos un recorrido histórico que comienza con el nacimiento de las matemáticas, con Pitágoras y su mujer Teano, y que continua con Hypatia en Alejandría, con Madame de Chatelet en Francia y con María Caetana Agnesi en Bolonia en el siglo XVIII. Incluso en el siglo XIX, Sophie Germain tuvo que adoptar la identidad de un antiguo alumno de la Escuela Politécnica de París, Monsieur Leblanc, para conseguir los materiales y problemas y para presentar sus propios resultados y trabajos. Sus trabajos sorprendieron a matemáticos de la altura de Lagrange y de Gauss. Ya a finales del siglo Sophia Kovaleskaya sufrió la marginación de la mujer en el mundo académico a pesar de ser uno de los mejores cerebros de la época.Sólo a las puertas del siglo XIX, una mujer Marie Curie va a realizar uno de los descubrimientos más importantes de la historia de la humanidad, un descubrimiento que va a cambiar la vida de ser humano en el siglo XX en muchos aspectos: la radioactividad. Y consiguió algo quizás tan importante: por primera vez en la historia la humanidad los círculos científicos abrían sus puertas de par en par a una mujer. Y con ella a tantas tan injustamente ignoradas durante siglos.
Cosmos y Caos: orden y desorden. Eso es lo que significan esas dos palabras griegas.La historia de la ciencia se reduce a esto: una lucha eterna por descubrir el funcionamiento de la Naturaleza, un intento interminable de poner orden en el caos. Y las matemáticas van a ser una herramienta imprescindible. Asistiremos a las batallas matemáticas más importantes en esta eterna guerra. Desde Pitágoras buscando en los números la armonía del Universo, hasta Platón asociando a los poliedros regulares el equilibrio universal. Nos detendremos en una batalla fundamental: la lucha de Copérnico, de Galileo y de Kepler por poner orden en le movimiento caótico de los planetas. Y seremos testigos del gran triunfo de Newton descubriendo el sistema del mundo, poniendo al mismo nivel a la manzana y a la Luna. Desde que Newton publicara en 1687 sus Principia Mathematica una idea va a impregnar hasta el último rincón de todas las disciplinas científicas: La Naturaleza tiene sus leyes matemáticas y el ser humano puede encontrarlas. Pero por desgracia la Naturaleza se guarda siempre alguna baza. Quién puede predecir cuándo y dónde se producirá un torbellino en una corriente de agua, cómo bailan las llamas de una hoguera, qué volutas va describir el humo de un cigarro, cuándo y dónde se formará una tormenta, dónde descargará un rayo, qué figura extraña dibujará en el cielo. Decididamente son fenómenos al otro lado de la frontera del caos. Pero las Matemáticas ya han puesto su avanzadilla en esa otra orilla: la teoría de Caos y la Geometría fractal. Caos y orden, orden y caos. ¿No serán en el fondo las dos caras de una misma y maravillosa moneda: la Naturaleza?
MÁS POR MENOS
El programa presenta a este exótico número ya conocido por los griegos. Veremos cómo se obtiene, qué son los rectángulos áureos y su presencia en infinidad de manifestaciones artísticas, en Pintura, Arquitectura, Escultura... a lo largo de la historia. Pero el número de oro no es un mero invento del hombre, la naturaleza nos sorprende de una forma que no puede ser casual, tanto en el mundo vegetal como en el animal, como en multitud de fenómenos físicos, con acontecimientos en los que este famosos número hace acto de presencia.
Nos introducimos en el atractivo mundo de la Geometría Dinámica. Todas las culturas han utilizado simetrías, traslaciones y giros en sus manifestaciones artísticas, han jugado, casi siempre con sorprendentes resultados plásticos, con los movimientos en el plano. La Naturaleza también nos brinda un exquisito muestrario de estos movimientos.La Geometría Dinámica se hace arte en los frisos y sobre todo en los mosaicos que rellenan el plano. En el programa investigamos la forma de construirlos y las leyes matemáticas que permiten realizar estas auténticas obras de arte.
Los frisos, mosaicos y adornos geométricos del arte hispano-musulman constituye una de las manifestaciones más espectaculares de la geometría en el Arte. Paseando por la Alhambra estudiaremos las técnicas para construir los mosaicos nazaríes deformando polígonos. De la mano del Prof. Rafael Pérez descubriremos que los artistas nazaríes conocían todas las formas posibles de rellenar el plano utilizando simetrías, giros y traslaciones. Otro gran genio, el pintor M.C. Escher, utiliza la técnica de rellenar el plano con motivos animados de una forma sorprendente e inquietante. Haremos una excursión por sus llamativos mosaicos y por sus mundos mágicos de geometrías imposibles.
Las espirales son unas de las curvas más sugerentes del mundo matemático. Las encontramos entre los motivos ornamentales de casi todas las culturas, desde las más remotas hasta la actualidad. Pero donde las espirales brillan de forma espectacular es en sus múltiples apariciones en la Naturaleza. En este programa descubriremos los distintos tipos de espirales y las formas de construirlas.
Las curvas que se obtienen al cortar una superficie cónica mediante un plano han cautivado a los matemáticos desde el tiempo de los griegos. Investigamos en este programa las propiedades y la manera de construirlas, sus manifestaciones y sus aplicaciones en campos tan dispares como la astronomía, las comunicaciones y los deportes.
Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo.
El ser humano siempre ha estado preocupado por lo que le deparará el futuro. Las matemáticas han intentado iluminar, al menos en parte, las pautas que rigen el futuro inmediato sujeto al azar. En nuestro país nos gastamos todas las semanas miles de millones de pesetas en loterías, bonolotos, primitiva, sorteos... Ponemos nuestra suerte y nuestro dinero en manos del azar. Pero el azar tiene sus leyes y en algunas de esas leyes profundizaremos en este programa. Descubriremos, entre otras, cosas la probabilidad de acertar un pleno en la primitiva. Lo que empezó como un juego, un problema de dados planteado a Pascal, se ha convertido en la Teoría de la Probabilidad, una de las herramientas matemáticas más utilizadas en la actualidad. Desde loa aficionados a los juegos de azar, hasta las aseguradoras y las multinacionales toman sus decisiones basándose en las Leyes del Azar.
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía.
El ordenador los ha puesto de moda. Y sin embargo ya eran conocidos a principios de siglo. Nos referimos a los fractales. Son los objetos matemáticos más atractivos, espectaculares y enigmáticos. A medio camino entre la linea y el plano, entre el plano y el espacio, rompen hasta con el concepto clásico de dimensión. Sus dimensiones no son números enteros, de ahí su extraño nombre. Y sin embargo se pueden obtener mediante simples iteracciones, es decir, repitiendo indefinidamente procedimientos geométricos o funcionales muy simples. Han dado origen a una nueva geometría: la geometría fractal. Una nueva herramienta matemática capaz de arrojar un poco de luz sobre los fenómenos caóticos y de mostrarnos que incluso en el caos es posible encontrar un determinado orden.
Cuando se anuncian unas elecciones una poderosa máquina matemática se pone en marcha. Es la Estadística a través de las encuestas y sondeos de opinión. Analizaremos en este programa los aspectos matemáticos más destacados de este tipo de sondeos y sus márgenes de fiabilidad. Pero después de depositar el voto las matemáticas siguen actuando. El sistema electoral español está basado en la ley D´Hont un sofisticado mecanismo en el que la aritmética interviene de forma determinante. Estudiaremos las características matemáticas de este sistema y su influencia en el mapa parlamentario en nuestro país.
Hay números que nos sorprenden por su tendencia a aparecer en las situaciones más inesperadas. ¿ Qué pueden tener en común los cables del tendido eléctrico, las cuentas bancarias, el desarrollo de una colonia de bacterias, la prueba del carbono 14 para datar restos orgánicos, las encuestas de población, la probabilidad de sacar 70 veces un número par al lanzar un dado 100 veces...? Aparentemente nada. Sin embargo en todas estas situaciones interviene un extraño número comprendido entre 2 y 3, que tiene infinitas cifras decimales y un origen un tanto exótico. Al igual que el más famoso número pi, los matemáticos le conocen mediante una letra. Es un número llamado e.
Las gráficas de contenido matemático se han convertido en el lenguaje más universal de finales del siglo XX. En cualquier medio de comunicación cada vez que se quiere dar información cuantitativa de un proceso aparece una gráfica matemática. Sus ventajas son incuestionables, son capaces de ofrecer gran cantidad de información de un simple vistazo. Constituyen un instrumento imprescindible en campos tan dispares como la medicina, la economía, la física, la biología y hasta en el deporte. En este programa investigaremos su origen relativamente reciente, tienen poco más de 200 años de existencia, y sus distintas aplicaciones y daremos algunos consejos para interpretar de forma crítica la información presentada en forma de gráficas.
La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles.

