Números Naturales (4ºESO-A)
De Wikipedia
| Revisión de 11:37 22 may 2008 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:43 22 may 2008 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| Podemos representarlos en una recta: | Podemos representarlos en una recta: | ||
| <center>[[Imagen:recta_naturales.png|500px]]</center> | <center>[[Imagen:recta_naturales.png|500px]]</center> | ||
| + | ==Jerarquía de las operaciones== | ||
| + | A la hora de operar con números naturales seguiremos las siguientes pautas: | ||
| + | {{Caja Amarilla|texto=Se efectúan primero el contenido de los '''paréntesis'''. De las operaciones, la de mayor prioridad es la '''potenciación''', seguida de la '''multiplicación''' y las '''división''' y, para terminar, la '''suma''' y la '''resta'''. | ||
| + | Si hay paréntesis anidados, se efectúan de dentro hacia fuera.}} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad Interactiva: ''Jerarquía de las operaciones''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=1. Operaciones combinadas. | ||
| + | |actividad= | ||
| + | En esta actividad debes escribir en la ventana bajo la escena el número que sigue al resolver la expresión y pulsar "intro". Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá. | ||
| + | |||
| + | Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final. | ||
| + | |||
| + | Al picar sobre inicio aparecerá otra expresión diferente de operaciones combinadas. Resuelve varias de ellas. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/naturales2/opcombin_1.html | ||
| + | width=450 | ||
| + | height=350 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Potenciación de naturales== | ||
| + | {{Caja Amarilla|texto= | ||
| + | Una potencia de '''base''' <math>a\;\!</math> y '''exponente''' <math>n\;\!</math> consiste en multiplicar <math>n\;\!</math> veces la base <math>a\;\!</math>. | ||
| + | <center><math>a^n =a \cdot a \cdots a\;\!</math></center>}} | ||
| + | {{p}} | ||
| + | |||
| + | Una potencia es un modo abreviado de escribir un producto de un número por sí mismo. | ||
| + | |||
| + | En la expresión de la potencia de un número consideramos dos partes: | ||
| + | |||
| + | * La '''base''' es el número que se multiplica por sí mismo | ||
| + | * El '''exponente''' es el número que indica las veces que la base aparece como factor. | ||
| + | |||
| + | Una potencia se escribe tradicionalmente poniendo el número base de tamaño normal y junto a él, arriba a su derecha se pone el exponente, de tamaño más pequeño. | ||
| + | |||
| + | Para nombrar o leer una potencia decimos primeramente el número base, después decimos lo referente al exponente. Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia". | ||
| + | |||
| + | {{AI2|titulo=Actividad Interactiva: ''Potencias''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1.''' Potencia de un número natural. | ||
| + | |actividad= | ||
| + | Observa cómo varía el resultado al modificar la base y el exponente. | ||
| + | {{p}} | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/potencia/definic_1.html | ||
| + | width=490 | ||
| + | height=230 | ||
| + | name=myframe | ||
| + | </iframe> | ||
| + | </center> | ||
| + | <center>[http://maralboran.ath.cx/web_ma/descartes/1y2_eso/potencia/definic_1.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | Haz uso de la escena anterior y contesta en tu cuaderno: | ||
| + | |||
| + | :a) ¿Qué valor tiene una potencia cuya base es el número 0 sea cual sea el exponente? | ||
| + | :b) ¿Qué valor tiene una potencia cuya base es el número 1 sea cual sea el exponente? | ||
| + | :c) ¿Qué valor tienen las potencias de cualquier base cuando su exponente es el número 0 ? | ||
| + | :d) ¿Qué valor tiene una potencia cuyo exponente es el número 1 ? | ||
| + | |||
| + | Cuando el exponente de una potencia es el número 1 no se pone exponente, basta con poner el número de la base | ||
| + | }} | ||
| + | }} | ||
Revisión de 11:43 22 may 2008
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora Números naturales |
Tabla de contenidos |
Números naturales
El conjunto de los números naturales es:
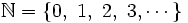
Son infinitos y sirven para contar (números cardinales: 1, 2, 3, ...) o para ordenar (números ordinales: 1º, 2º, 3º, ...).
Representación de los números naturales
Podemos representarlos en una recta:
Jerarquía de las operaciones
A la hora de operar con números naturales seguiremos las siguientes pautas:
Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
|
Actividad Interactiva: Jerarquía de las operaciones
1. Operaciones combinadas.
Actividad: En esta actividad debes escribir en la ventana bajo la escena el número que sigue al resolver la expresión y pulsar "intro". Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá. Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final. Al picar sobre inicio aparecerá otra expresión diferente de operaciones combinadas. Resuelve varias de ellas. |
Potenciación de naturales
Una potencia de base  y exponente
y exponente  consiste en multiplicar
consiste en multiplicar  veces la base
veces la base  .
.
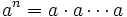
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo.
En la expresión de la potencia de un número consideramos dos partes:
- La base es el número que se multiplica por sí mismo
- El exponente es el número que indica las veces que la base aparece como factor.
Una potencia se escribe tradicionalmente poniendo el número base de tamaño normal y junto a él, arriba a su derecha se pone el exponente, de tamaño más pequeño.
Para nombrar o leer una potencia decimos primeramente el número base, después decimos lo referente al exponente. Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
|
Actividad Interactiva: Potencias
Actividad 1. Potencia de un número natural.
Actividad: Observa cómo varía el resultado al modificar la base y el exponente. Haz uso de la escena anterior y contesta en tu cuaderno:
|


