Trigonometría (PACS)
De Wikipedia
| Revisión de 18:41 24 sep 2008 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:45 24 sep 2008 Juanmf (Discusión | contribuciones) (→Ángulo llano o extendido) Ir a siguiente diferencia → |
||
| Línea 46: | Línea 46: | ||
| Un ángulo obtuso es aquel cuya amplitud es mayor a <math>\frac{\pi}{2}</math> [[radian|rad]] y menor a <math>\pi\,</math> rad (mayor a 90º y menor a 180º). | Un ángulo obtuso es aquel cuya amplitud es mayor a <math>\frac{\pi}{2}</math> [[radian|rad]] y menor a <math>\pi\,</math> rad (mayor a 90º y menor a 180º). | ||
| - | === Ángulo llano o extendido === | ||
| - | El ángulo llano tiene una amplitud de <math> \pi \,</math> [[radian|rad]] (equivalente a 180º). | ||
| - | [[Imagen:Ángulo cóncavo.svg|thumb|120px|left|Ángulo cóncavo]] | ||
| - | [[Imagen:Ángulo completo.svg|thumb|120px|Ángulo completo]] | ||
| === Ángulo cóncavo o reflejo === | === Ángulo cóncavo o reflejo === | ||
Revisión de 18:45 24 sep 2008
| Enlaces internos | Para repasar | Enlaces externos |
| Indice CD Alumno 07 Resueltos 07 Descartes Manual Casio | Trigonometría (ppt) | WIRIS Calculadora |
La trigonometría en principio es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para esto se vale de las razones trigonométricas, las cuales son utilizadas frecuentemente en cálculos técnicos. En términos generales, la trigonometría es el estudio de las funciones seno, coseno, tangente, cotangente, secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.
Se denomina ángulo, en el plano, a la porción de éste comprendida entre dos semirrectas que tienen un origen común denominado vértice. Coloquialmente, ángulo es la figura formada por dos rayos con origen común. Así, un ángulo determina una superficie abierta (subconjunto abierto de puntos del plano), al estar definido por dos semirrectas, denominándose medida del ángulo a la amplitud de estas semirrectas.
Tabla de contenidos |
Las unidades de medida de ángulos
Las unidades utilizadas para la medida de los ángulos del plano son:
- Radián (usado oficialmente en el sistema internacional de unidades)
- Grado centesimal
- Grado sexagesimal
Los ángulos se pueden medir mediante utensilios tales como el goniómetro, el cuadrante, el sextante, la ballestina, el transportador de ángulos o semicírculo graduado, etc.
Clasificación de ángulos planos
Ángulo agudo
Es el ángulo formado por dos semirrectas con amplitud mayor de 0 rad y menor de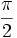 
rad (mayor de 0º y menor de 90º).
Al punto de inicio o de encuentro, se le llama vértice.
Ángulo recto
- Un ángulo recto es de amplitud igual a 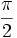rad (equivalente a 90º).
- Un ángulo recto es de amplitud igual a
- Los dos lados de un ángulo recto son perpendiculares entre sí.
La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice.
- Los dos lados de un ángulo recto son perpendiculares entre sí.
Ángulo obtuso
Un ángulo obtuso es aquel cuya amplitud es mayor a 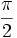rad y menor a 
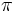rad (mayor a 90º y menor a 180º).
Ángulo cóncavo o reflejo
El ángulo cóncavo, externo o reflejo, es el que mide más de 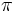rad y menos de 
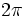rad (esto es, más de 180º y menos de 360°)
Ángulo completo o perigonal
Un ángulo completo o perigonal, tiene una amplitud de 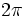rad (equivalente a 360º)
Ángulos relacionados
En función de su posición, se denominan:
- ángulos adyacentes, los que tienen un vértice y un lado común, pero no tienen ningún punto interior común,
- ángulos consecutivos, los que tienen un lado y el vértice común,
- ángulos opuestos por el vértice, aquellos cuyos lados son semirrectas opuestas.
En función de su amplitud, se denominan:
- ángulos congruentes, aquellos que tienen la misma amplitud,
- ángulos complementarios, aquellos cuya suma de medidas es π/2 radianes o 90º,
- ángulos suplementarios, aquellos cuya suma de medidas es π radianes o 180º,
- ángulos conjugados, aquellos cuyas medidas suman 2π radianes o 360º.
Ángulos de un polígono
En función de su posición, se denominan:
- ángulo interior o interno de un polígono, es el formado por lados adyacentes, interiormente,
- ángulo exterior o externo de un polígono, es el conformado por un lado y la prolongación del adyacente.
Ángulos respecto de una circunferencia
Un ángulo, respecto de una circunferencia, pueden ser:
Ángulo central, si tiene su vértice en el centro de ésta.
- La amplitud de un ángulo central es igual a la del arco que abarca.
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados la cortan en dos puntos.
- La amplitud de un ángulo inscrito es la mitad de la del arco que abarca. (Véase: arco capaz.)
Ángulo semi-inscrito, si su vértice está sobre ésta, uno de sus lados la corta y el otro es tangente, siendo el punto de tangencia el propio vértice.
- La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.
Ángulo interior, si su vértice está en el interior de la circunferencia.
- La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones;
Ángulo exterior, si tiene su vértice en el exterior de ésta.
- La amplitud de un ángulo exterior es la mitad de la diferencia de los dos arcos que abarcan sus lados sobre dicha circunferencia.
