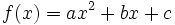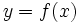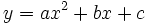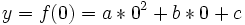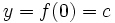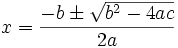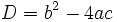Funciones Cuadráticas (PACS)
De Wikipedia
| Revisión de 13:48 27 sep 2008 Juanmf (Discusión | contribuciones) (→Definición) ← Ir a diferencia anterior |
Revisión actual Juanmf (Discusión | contribuciones) |
||
| Línea 2: | Línea 2: | ||
| |ir= | |ir= | ||
| |ampliar= | |ampliar= | ||
| - | |repasar=[http://maralboran.org/web_ma/presentaciones/funciones2.ppt Funciones (ppt)] | + | |repasar=[http://maralboran.org/web_ma/presentaciones/funciones2.ppt Funciones (ppt)]<br>[http://www.maralboran.org/web_ma/descartes/Analisis/Funciones_matematicas/indice.htm Descartes: Funciones matemáticas] |
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| Línea 15: | Línea 15: | ||
| donde '''a''', '''b''' y '''c''' son constantes y '''a''' distinto de 0. | donde '''a''', '''b''' y '''c''' son constantes y '''a''' distinto de 0. | ||
| }} | }} | ||
| - | la representación gráfica en el plano '''xy''' haciendo: | + | '''La representación gráfica''' en el plano '''xy''' haciendo: |
| : <math> y = f(x) \, </math> | : <math> y = f(x) \, </math> | ||
| Línea 71: | Línea 71: | ||
| En la vertical que pasa por este valor de '''x''' se encontrara el valor máximo o mínimo de la función. | En la vertical que pasa por este valor de '''x''' se encontrara el valor máximo o mínimo de la función. | ||
| + | |||
| + | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice CD Alumno 07 Resueltos 07 Descartes Manual Casio | Funciones (ppt) Descartes: Funciones matemáticas | WIRIS Calculadora |
Tabla de contenidos |
Definición
Una función cuadrática es la que corresponde a un polinomio en x de segundo grado, según la forma:
donde a, b y c son constantes y a distinto de 0.
La representación gráfica en el plano xy haciendo:
esto es:
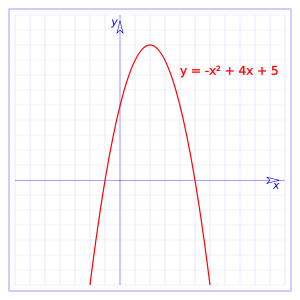
es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de a.
Estudio de la función
Corte con el eje y
La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):
lo que resulta:
la función corta el eje y en el punto (0, c), siendo c el termino independiente de la función.
Corte con el eje x
La función corta al eje x cuando y vale 0:
las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen como es sabido por la expresión:
donde:
se le llama discriminante, D:
según el signo del discriminante podemos distinguir:
- D > 0
La ecuación tiene dos soluciones, por tanto la parábola cortara al eje x en dos puntos: 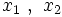
- D = 0
La ecuación tiene una solución, la parábola solo tiene un punto en común con el eje x, en la cual es tangente a este eje donde las dos ramas de la parábola confluyen.
- D < 0
La ecuación no tiene solución real, y la parábola no corta al eje x.
Extremos relativos
Para localizar los extremos relativos, se calcula x:
En la vertical que pasa por este valor de x se encontrara el valor máximo o mínimo de la función.