Límite de una sucesión (1ºBach)
De Wikipedia
| Revisión de 16:32 11 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:33 11 ene 2009 Coordinador (Discusión | contribuciones) (→Representación gráfica de una sucesión) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| {{p}} | {{p}} | ||
| {{Ejemplo | {{Ejemplo | ||
| - | |titulo=Ejemplo: ''Representación gráfica de una sucesión'' | + | |titulo=Ejemplos: ''Representación gráfica de una sucesión'' |
| |enunciado=Representa graficamente las siguientes sucesiones: | |enunciado=Representa graficamente las siguientes sucesiones: | ||
| ::a) <math> a_{n} = \cfrac{16}{2^n}</math> | ::a) <math> a_{n} = \cfrac{16}{2^n}</math> | ||
| Línea 95: | Línea 95: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Aproximación a la idea de límite de una sucesión== | ==Aproximación a la idea de límite de una sucesión== | ||
| ==Sucesiones que no tienen límite== | ==Sucesiones que no tienen límite== | ||
| [[Categoría: Matemáticas]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión de 16:33 11 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Para acercarnos a la idea de límite, vamos a empezar viendo algunas representaciones gráficas de sucesiones
Representación gráfica de una sucesión
Para representar gráficamente una sucesión 
, construiremos una tabla donde anotaremos el valor de para valores distintos valores de n.
Las parejas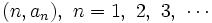 
obtenidas en la tabla, son las coordenadas de los puntos de la representación gráfica de la sucesión, que dibujaremos en unos ejes de coordenadas cartesianos.
Ejemplos: Representación gráfica de una sucesión
Representa graficamente las siguientes sucesiones:
- a)
- b)
- a)
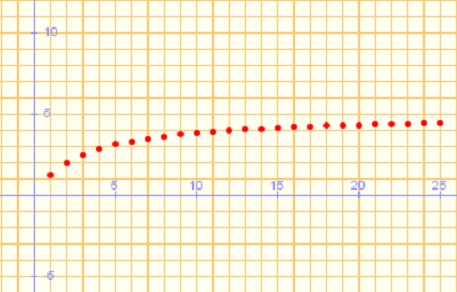
| a)
Construimos la tabla de valores:
Se observa que los términos de la sucesión se acercan cada vez mas a 0. Concluiremos diciendo que el límite de esta sucesión es 0, y lo escribiremos simbólicamente de la siguiente manera:  |  |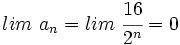
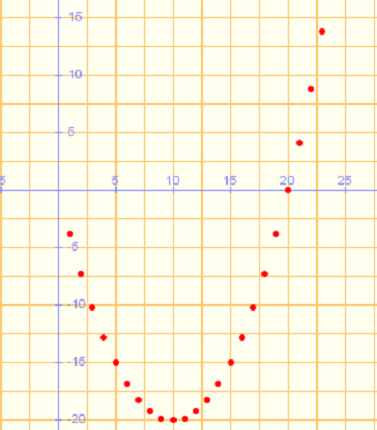
| b)
Construimos la tabla de valores:
Se observa que los términos crecen y se hacen indefinidamente grandes. Concluiremos diciendo que el límite de esta sucesión es  |  |
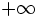, y lo escribiremos simbólicamente de la siguiente manera:
