Algunos límites importantes (1ºBach)
De Wikipedia
| Revisión de 19:22 12 ene 2009 Coordinador (Discusión | contribuciones) (→El número ''e'') ← Ir a diferencia anterior |
Revisión de 19:25 12 ene 2009 Coordinador (Discusión | contribuciones) (→El número ''e'') Ir a siguiente diferencia → |
||
| Línea 66: | Línea 66: | ||
| ==El número ''e''== | ==El número ''e''== | ||
| - | {{Tabla75|celda2=[[Imagen:Eukler1.jpg|thumb|[[Euler|Leonard Euler]]: El número '''e''', base de los logaritmos neperianos, lleva este nombre en su honor (inicial de su apellido)]] | + | {{Tabla75 |
| + | |celda2= | ||
| + | <center>[[Imagen:Eukler1.jpg|thumb|[[Euler|Leonard Euler]]: El número '''e''', base de los [[logaritmos|Logaritmos (1ºBach)]] neperianos, lleva este nombre en su honor (inicial de su apellido)]]</center> | ||
| |celda1= | |celda1= | ||
| {{Teorema|titulo=''La sucesión del número e'' | {{Teorema|titulo=''La sucesión del número e'' | ||
Revisión de 19:25 12 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Suma de los términos de una progresión geométrica
Límite de la suma de n primeros términos de una progresión geométrica
Sea  una progresión geométrica de razón
una progresión geométrica de razón  y sea
y sea 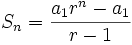 la suma de sus n primeros términos
la suma de sus n primeros términos
- Si
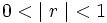 , entonces el límite de
, entonces el límite de 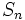 existe y su valor es:
existe y su valor es:
- Si
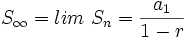
- Si
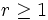 , entonces el límite de
, entonces el límite de 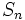 es
es 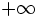 o
o  :
:
- Si
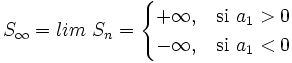
- Si
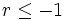 , entonces el límite de
, entonces el límite de 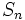 no existe.
no existe.
- Si
- Si
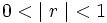 , entonces
, entonces
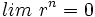 y también
y también 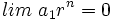 .
.(Por ejemplo, si a1 = 3 y r = 0.5, al multiplicar sucesivas veces 3 por 0.5, lo que equivale a dividir por 2, el resultado se aproxima cada vez más a cero.)
y por tanto
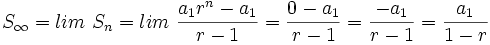
- Si
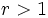 , entonces
, entonces
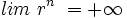 y
y 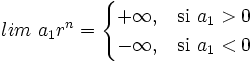
(Por ejemplo, si a1 = 3 y r = 5, al multiplicar sucesivas veces 3 por 5, el resultado se aproxima cada vez más a  . Mientras que si a1 = − 3 y r = 5, al multiplicar sucesivas veces -3 por 5, el resultado se aproxima cada vez más a
. Mientras que si a1 = − 3 y r = 5, al multiplicar sucesivas veces -3 por 5, el resultado se aproxima cada vez más a  )
)
y por tanto
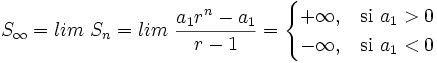
- Si
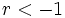 , entonces
, entonces 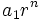 va alternando valores positivos y negativos, cada vez mayores en valor absoluto, de manera que a la sucesión
va alternando valores positivos y negativos, cada vez mayores en valor absoluto, de manera que a la sucesión 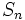 también va a oscilar en signo y no tiene límite.
también va a oscilar en signo y no tiene límite.
- Si
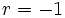 , el caso es muy sencillo, porque la progresión quedaría:
, el caso es muy sencillo, porque la progresión quedaría:
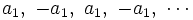
y la sucesión 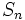 sería:
sería:
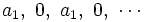
que oscila y no tiene límite.
- Si
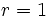 , la progresión quedaría constante:
, la progresión quedaría constante:
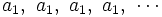 , .
, .y tendríamos que 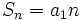 , cuyo límite es:
, cuyo límite es:
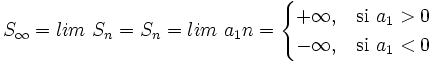
El número e
La sucesión del número e El número 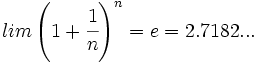 (número e) (número e)Demostración: Es inmediato hacer una comprobación dando valores a n, cada vez más grandes. Así obtendríamos: 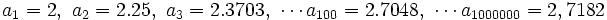 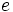 Video: Un número llamado e (13´) Sinopsis: Hay números que nos sorprenden por su tendencia a aparecer en las situaciones más inesperadas. ¿Qué pueden tener en común los cables del tendido eléctrico, las cuentas bancarias, el desarrollo de una colonia de bacterias, la prueba del carbono 14 para datar restos orgánicos, las encuestas de población, la probabilidad de sacar 70 veces un número par al lanzar un dado 100 veces...? Aparentemente nada. Sin embargo en todas estas situaciones interviene un extraño número comprendido entre 2 y 3, que tiene infinitas cifras decimales y un origen un tanto exótico. Al igual que el más famoso número pi, los matemáticos le conocen mediante una letra. Es un número llamado e. |  Leonard Euler: El número e, base de los Logaritmos (1ºBach) neperianos, lleva este nombre en su honor (inicial de su apellido) |
El número áureo, 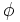
La sucesión de Fibonacci y el número áureo
Si a partir de la sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...), construimos, por recurrencia, la sucesión 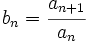 , se cumple que:
, se cumple que:
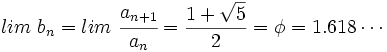 (número áureo)
(número áureo)Lo siguiente no es una demostración, sino una comprobación:
En efecto, si en la sucesión de Fibonacci
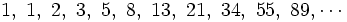
dividimos cada término entre el anterior, tenemos:
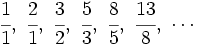
que expresada con decimales nos da:
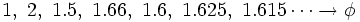
Video: La divina proporción. El número Phi. (6´)
Documental sobre la historia del número áureo, Phi
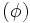 y la divina proporción.
y la divina proporción.Web: [Phi, el número de oro Phi, el número de oro]
A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz.

