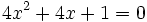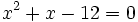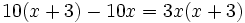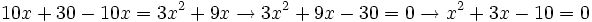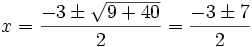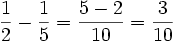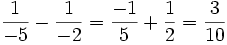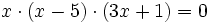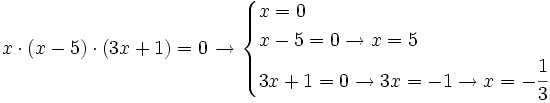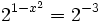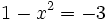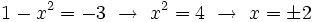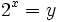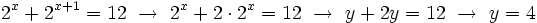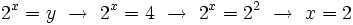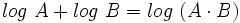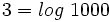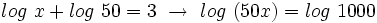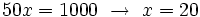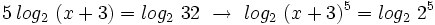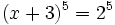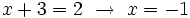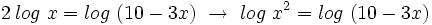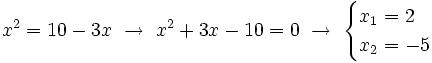Resolución de ecuaciones (1ºBach)
De Wikipedia
| Revisión de 18:46 14 ene 2009 Coordinador (Discusión | contribuciones) (→Ecuación de segundo grado) ← Ir a diferencia anterior |
Revisión de 18:49 14 ene 2009 Coordinador (Discusión | contribuciones) (→Ecuaciones bicuadradas) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| ==Ecuaciones bicuadradas== | ==Ecuaciones bicuadradas== | ||
| - | {{Caja_Amarilla|texto= | + | {{Ecuaciones bicuadradas |
| - | Las '''ecuaciones bicuadradas''' Son ecuaciones de cuarto grado pero tienen una característica que las hace especiales: no tienen terminos de grado impar, es decir son de la forma | + | {{p}}}} |
| - | <center><math>ax^4 + bx^2 +c = 0\,\!</math></center> | + | |
| - | + | ||
| - | El truco para resolverlas es hacer el cambio de variable <math>x^2=y\,\!</math>. Entonces, la ecuación quedará como una de segundo grado | + | |
| - | + | ||
| - | <center><math>ay^2 + by + c = 0 \,\!</math></center> | + | |
| - | + | ||
| - | Una vez resuelta esta ecuación en <math>y\;</math>, tenemos que averiguar el valor de la <math>x\;</math>. Para ello desharemos el cambio de variable, haciendo <math>x=\pm \sqrt{y}</math>. En consecuencia, las soluciones <math>y<0\,\!</math>, las rechazaremos, ya que no darán solución para la <math>x\,\!</math>, quedándonos sólo con las soluciones de <math>y\,\!</math> no negativas, cada una de las cuales dará dos soluciones para la <math>x\,\!</math>.}} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Ecuaciones bicuadradas'' | + | |
| - | |enunciado=Resuelve las ecuaciones: | + | |
| - | ::a) <math>x^4 - 7x^2 + 6 = 0\;\! </math> | + | |
| - | ::b) <math>x^4 - 3x^2 - 10 = 0\;\! </math> | + | |
| - | ::c) <math>x^4 - 9x^2 = 0 \;\! </math> | + | |
| - | |sol= | + | |
| - | a) <math>x^4 - 7x^2 + 6 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-7y+6=0</math> | + | |
| - | + | ||
| - | <math>y = \frac{7 \pm \sqrt{49-24}}{2}=\frac{7 \pm 5}{2} \rightarrow \begin{cases} y=1 \rightarrow x= \pm \sqrt 1 = \pm 1 \\ y=6 \rightarrow x= \pm \sqrt 6 \end{cases}</math> | + | |
| - | + | ||
| - | '''Soluciones:''' <math>-1,\, 1,\, -\sqrt 6,\, \sqrt 6\,\!</math> | + | |
| - | {{p}} | + | |
| - | ---- | + | |
| - | b) <math>x^4 - 3x^2 - 10 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-3y-10=0</math> | + | |
| - | + | ||
| - | <math>y = \frac{3 \pm \sqrt{9+40}}{2}=\frac{3 \pm 7}{2} \rightarrow \begin{cases} y=-2 \rightarrow \mbox {No existe solucion para x} \\ y=5 \rightarrow x= \pm \sqrt 5 \end{cases}</math> | + | |
| - | + | ||
| - | '''Soluciones:''' <math> -\sqrt 5,\, \sqrt 5\,\!</math> | + | |
| - | {{p}} | + | |
| - | ---- | + | |
| - | c) <math>x^4 - 9x^2 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-9y=0</math> | + | |
| - | + | ||
| - | <math> y(y-9)=0 \rightarrow \begin{cases} y=0 \rightarrow x= 0 \\ y=9 \rightarrow x= \pm \sqrt 9 = \pm 3 \end{cases}</math> | + | |
| - | + | ||
| - | '''Soluciones:''' <math>0,\, -3,\, 3\,\!</math> | + | |
| - | }} | + | |
| ==Ecuaciones con la x en el denominador== | ==Ecuaciones con la x en el denominador== | ||
Revisión de 18:49 14 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Ecuación de segundo grado
Ecuación de segundo grado
- Una ecuación de segundo grado con una incógnita,
 , es aquella que tiene o se puede reducir a la siguiente expresión, que llamaremos forma general.
, es aquella que tiene o se puede reducir a la siguiente expresión, que llamaremos forma general.
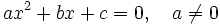
- Si algún coeficiente,"b" o "c", es cero la ecuación diremos que es incompleta. En caso contrario diremos que es completa.
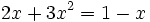 es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general:
es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general: 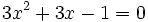
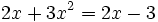 es una ecuación de segundo grado incompleta, ya que se puede reducir a la siguiente forma general:
es una ecuación de segundo grado incompleta, ya que se puede reducir a la siguiente forma general: 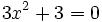
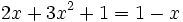 es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general:
es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general: 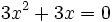
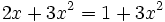 no es una ecuación de segundo grado, ya que al reducirla resulta una ecuación de primer grado:
no es una ecuación de segundo grado, ya que al reducirla resulta una ecuación de primer grado: 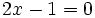
Definición de ecuación de segundo grado.
Actividades en la que aprenderás a identificar los coeficientes de una ecuación de segundo grado y a determinar si es completa o incompleta.
El siguiente videotutorial condensa casi todo lo que se va a tratar en este tema:
- Definición de ecuación de segundo grado.
- Fórmula para su resolución con su demostración.
- Definición de discriminante de una ec. de segundo grado y su relación con el número de soluciones de ésta y con ejemplos de cada caso.
- Factorización del polinomio de segundo grado a partir de las soluciones o raíces de la ecuación de segundo grado.
- Propiedades del producto y la suma de las raíces de la ecuación con su demostración.
- Ecuaciones de segundo grado incompletas.
Ecuación de segundo grado completa
Fórmula general
Las soluciones de la ecuación de segundo grado
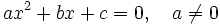
son:
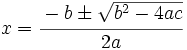
donde el signo 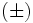 significa que una solución se obtiene con el signo
significa que una solución se obtiene con el signo 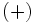 y otra con el signo
y otra con el signo 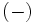 .
.
A continuación tienes la demostración en videtutorial y por escrito:
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Demostración:
1. Se divide la ecuación por  :
:
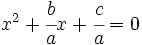
2. Se multiplica y divide por  el coeficiente de la
el coeficiente de la  :
:
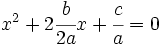
3. Se suma a los dos miembros de la igualdad 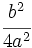 :
:
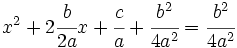
4. Se pasa restando a la derecha  :
:
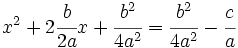
5. Observando que el lado izquierdo es el desarrollo de 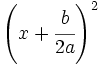 :
:
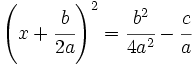
6. Se extrae la raíz cuadrada en ambos miembros:
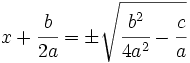
7. Se despeja x:
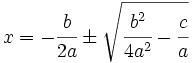
8. Se simplifica la expresión:
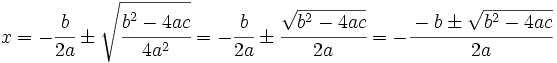
En la escena, pulsa "Inicio" para ver otros ejemplos.
Cómo utilizar la fórmula general de la ecuación de segundo grado.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Tutorial en el que se explica la resolución de ecuaciones de 2º grado aplicando la fórmula general de resolución.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Escribe en forma general e identifica los coeficientes "a", "b", y "c": 6x2 + 3 = 2x − 6.
Resuelve usando la fórmula: − x2 + 8x = 1.
Resuelve usando la fórmula: − 3x2 + 10x − 3 = 0.
Resuelve usando la fórmula: − 7q2 + 2q + 9 = 0.
Actividades en la que aprenderás a resolver ecuaciones de segundo grado completas.
Actividades en la que aprenderás a resolver ecuaciones de segundo grado completas.
Resolver ecuaciones de segundo grado completas.
Ejercicios de autoevaluación sobre ecuaciones de segundo grado completas.
- Pulsa el botón "Ejercicio" para obtener una ecuación.
- Copia la ecuación en tu cuaderno y halla sus soluciones.
- Escribe el "tipo de solución" y las soluciones en los cuadros correspondientes. Luego pulsa el botón "Solución".
Ejercicios resueltos sobre ecuaciones de segundo grado completas.
Número de soluciones de la ecuación de segundo grado
Llamamos discriminante de una ecuación de segundo grado, 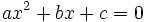 , al número:
, al número:
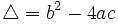
Proposición
Sea  el discriminante de una ecuación de segundo grado:
el discriminante de una ecuación de segundo grado:
- Si
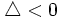 , la ecuación no tiene solución.
, la ecuación no tiene solución.
- Si
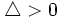 , la ecuación tiene dos soluciones.
, la ecuación tiene dos soluciones.
- Si
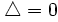 , la ecuación tiene una solución (doble).
, la ecuación tiene una solución (doble).
La demostración es inmediata teniendo en cuenta la fórmula para la resolución de la ecuación de segundo grado:
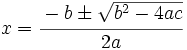
ya que, lo que hay en el radicando, es precisamente el discriminante. Por tanto,
- Si su signo es positivo, la raíz existe y da lugar a dos soluciones distintas.
- Si su signo es negativo, la raíz no existe y no hay ninguna solución.
- Si es cero, la raíz vale cero, y hay dos soluciones iguales (solución doble).
Número de soluciones de una ecuación de 2º grado. Discriminante.
Halla el discriminante para determinar el número de raíces de la ecuación 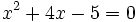 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 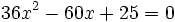 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 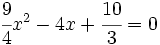 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 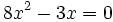 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 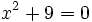 .
.
Determinar el número de soluciones de la ecuación 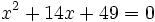 .
.
Actividades en la que aprenderás a calcular el discriminante de una ecuación de segundo grado y su utilidad para determinar el número de soluciones de la misma.
Calcula el número de soluciones de una ecuación de segundo grado:
- Pulsa el botón "Ejercicio" para obtener una ecuación.
- Copia la ecuación en tu cuaderno y calcula su discriminante.
- Teniendo en cuenta el valor del discriminante, determina cuántas soluciones tiene.
- Escribe el número de soluciones en el cuadro "Número de soluciones" y pulsa el botón "Solución".
Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.
Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado, 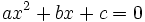 , es incompleta, si
, es incompleta, si 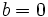 ó
ó 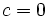 :
:
- Si
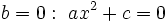
- Si
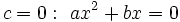
Resolución de las ecuaciones de segundo grado incompletas
- En el caso
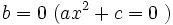 , las soluciones se obtienen despejando
, las soluciones se obtienen despejando  :
:
- En el caso
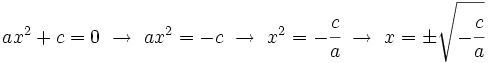
- En el caso
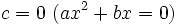 , las soluciones se obtienen sacando factor común e igualando a cero cada factor:
, las soluciones se obtienen sacando factor común e igualando a cero cada factor:
- En el caso
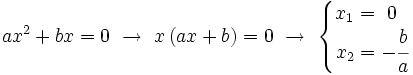
En la escena, pulsa "INICIO" para ver otros ejemplos.
En la escena, pulsa "INICIO" para ver otros ejemplos.
Ecuaciones de segundo grado sin termino lineal (caso b=0). Ejemplos.
Ecuaciones de segundo grado sin termino independiente (caso c=0). Ejemplos.
Ecuaciones de segundo grado incompletas (caso b=0)
Ecuaciones de segundo grado incompletas (caso c=0)
Ecuaciones de segundo grado incompletas (caso b=0):
Resuelve: 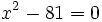
Resuelve: 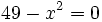
Resuelve: 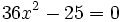
Resuelve: 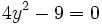
Ecuaciones de segundo grado incompletas (caso c=0):
Resuelve: 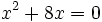
Resuelve: 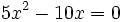
Resuelve: 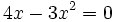
Actividades en la que aprenderás a resolver ecuaciones de segundo grado incompletas del tipo b=0.
Actividades en la que aprenderás a resolver ecuaciones de segundo grado incompletas del tipo c=0.
Ejercicios de autoevaluación sobre ecuaciones de segundo grado incompletas.
Ejercicios resueltos sobre ecuaciones de segundo grado incompletas.
Ecuaciones bicuadradas
{{Ecuaciones bicuadradas
}}Ecuaciones con la x en el denominador
Las ecuaciones que tienen la incógnita en el denominador, laspuedes resolver de forma análoga a las que tienen números en el denominador, es decir, haciendo el mínimo común múltiplo de los denominadores. A continuación se divide el m.c.m. entre cada denominador y se multiplica el resultado por su respectivo numerador, Esto se hace con los dos miembros de la ecuación.De esta forma desaparecen los denominadores y la ecuación resultante ya es más sencilla de resolver.
En estos procesos de multiplicar los miembros de la ecuación por polinomios, pueden aparecer soluciones falsas. Por tanto, al terminar, siempre debemos comprobar todas las posibles soluciones obtenidas.
Ejemplo: Ecuaciones con x en el denominador
Resuelve las ecuación: 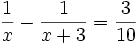
El m.c.m. de los denominadores es 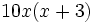 . Lo dividimos por cada denominador y multiplicamos el resultado por el numerador, de manera que los denominadores desaparecen:
. Lo dividimos por cada denominador y multiplicamos el resultado por el numerador, de manera que los denominadores desaparecen:
Simplificamos la ecuación resultante:
Y la resolvemos:
Hay dos soluciones:  y
y 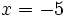 . Ambas se deben comprobar en la ecuación inicial y resultan ser válidas:
. Ambas se deben comprobar en la ecuación inicial y resultan ser válidas:
Ecuaciones con radicales
Las ecuaciones con radicales son aquellas que tienen la x dentro de raices cuadradas. Para solucionarlas hay que aislar las raices una a una e ir elevando al cuadrado para eliminarlas.
Al elevar al cuadrado para buscar la solución, pueden aparecer soluciones erroneas. Por eso, al finalizar, hay que hacer la comprobación en la ecuación inicial para detectar y recharzar las que no sean válidas.
Ejemplo: Ecuaciones con radicales
Resuelve las ecuaciones:
- a)
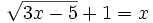
- a)
- b)
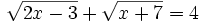
- b)
a) 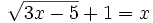
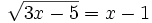
Se elevan al cuadrado los dos lados de la ecuación:
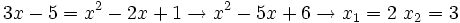
Comprobación: 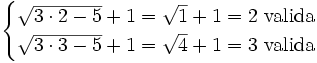
b) 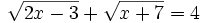
Despejamos la primera raíz (Podíamos haber empezado por la segunda)
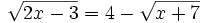
Se elevan al cuadrado los dos lados del igual
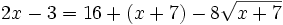
Aislamos la raíz
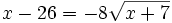
Se elevan al cuadrado los dos lados del igual
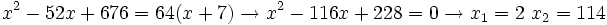
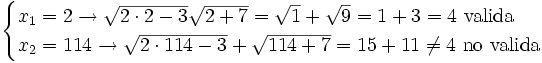
Ecuaciones factorizadas
Las ecuaciones factorizadas son ecuaciones del tipo:
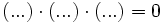
donde cada factor 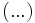 es una expresión algebraica.
es una expresión algebraica.
Como para que un producto sea cero basta con que uno de los factores sea cero, tenemos que igualar a cero cada factor y resolver la ecuación resultante.
Ecuaciones exponenciales
Las ecuaciones exponenciales son aquellas en las que la incógnita aparece como exponente.
Ejemplo: Ecuación exponencial
Resuelve las siguientes ecuaciónes:
- a)
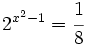
- a)
- b)
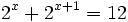
- b)
a) 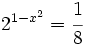
Expresamos el segundo miembro como potencia de 2:
Como 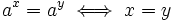 , los exponentes deben ser iguales:
, los exponentes deben ser iguales:
Y resolvemos la ecuación de segundo grado incompleta:
Soluciones: 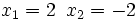
b) 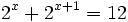
Hacemos el siguiente cambio de variable:
Así nuestra ecuación queda:
Ahora hay que deshacer el cambio de variable:

Ecuaciones logarítmicas
Las ecuaciones logarítmicas son aquellas en las que la incógnita aparece como parte de un logaritmo.
Para su resolución hay que tener en cuenta las propiedades de los logaritmos.
Ejemplos: Ecuaciones logarítmicas
Resuelve las siguientes ecuaciónes:
- a)
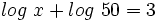
- a)
- b)
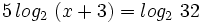
- b)
- c)
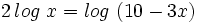
- c)
a) 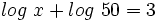
Teniendo en cuenta que:
tenemos:
Y teniendo en cuenta que 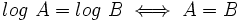 , se tiene:
, se tiene:
Solución: 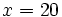
b) 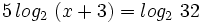
Teniendo en cuenta que:
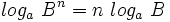 , tenemos:
, tenemos:
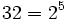
tenemos:
Como 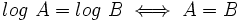 , se tiene:
, se tiene:
Y, como 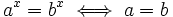
Solución: 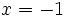
c) 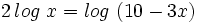
Teniendo en cuenta que 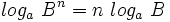 , tenemos:
, tenemos:
Como 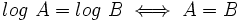 , se tiene:
, se tiene:
De las dos soluciones, 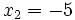 no es válida, porque al comprobarla en la ecuación de partida,
no es válida, porque al comprobarla en la ecuación de partida, 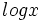 no se puede calcular para
no se puede calcular para 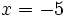 (El logaritmo de un número negativo no existe).
(El logaritmo de un número negativo no existe).
Solución: