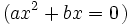Plantilla:Ecuación de segundo grado
De Wikipedia
| Revisión de 19:01 14 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:22 14 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 18: | Línea 18: | ||
| {{p}} | {{p}} | ||
| - | ==Resolución de la ecuación de segundo grado== | + | ===Resolución de la ecuación de segundo grado=== |
| {{Teorema|titulo=''Fórmula de la ecuación de segundo grado'' | {{Teorema|titulo=''Fórmula de la ecuación de segundo grado'' | ||
| |enunciado=Las soluciones de la ecuación de segundo grado son: | |enunciado=Las soluciones de la ecuación de segundo grado son: | ||
| Línea 65: | Línea 65: | ||
| {{p}} | {{p}} | ||
| - | ==Discriminante de una ecuación de segundo grado== | + | ===Discriminante de una ecuación de segundo grado=== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Llamamos '''discriminante''' de una ecuación de segundo grado a: | Llamamos '''discriminante''' de una ecuación de segundo grado a: | ||
| Línea 76: | Línea 76: | ||
| {{p}} | {{p}} | ||
| - | ==Ecuaciones de segundo grado incompletas== | + | ===Ecuaciones de segundo grado incompletas=== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Una ecuación de segundo grado <math>ax^2+bx+c=0\;\!</math> es incompleta, si ocurre uno de los siguientes casos: | Una ecuación de segundo grado <math>ax^2+bx+c=0\;\!</math> es incompleta, si ocurre uno de los siguientes casos: | ||
Revisión de 19:22 14 ene 2009
Una ecuación de segundo grado con una incógnita,  , es aquella que tiene la siguiente expresión, que llamaremos forma general.
, es aquella que tiene la siguiente expresión, que llamaremos forma general.
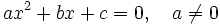
Ejemplo: Ecuación de segundo grado
Pasa a forma general la ecuación:
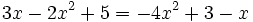
Para ponerla en forma general, pasaremos todos los términos al miembro de la izquierda:
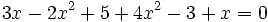
Agrupando términos semejantes:
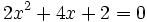
Resolución de la ecuación de segundo grado
Fórmula de la ecuación de segundo grado
Las soluciones de la ecuación de segundo grado son:
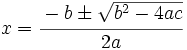
donde el signo 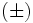 significa que una solución se obtiene con el signo
significa que una solución se obtiene con el signo 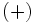 y otra con el signo
y otra con el signo 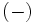 .
.
1. Se divide la ecuación por  :
:
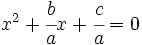
2. Se multiplica y divide por  el coeficiente de la
el coeficiente de la  :
:
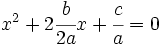
3. Se suma alos dos miembros de la igualdad 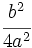 :
:
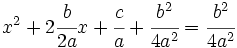
4. Se pasa restando a la derecha  :
:
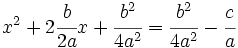
5. Observando que el lado izquierdo es el desarrollo de 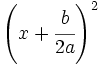 :
:
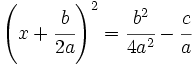
6. Se extrae la raíz cuadrada en ambos miembros:
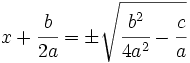
7. Se despeja x:
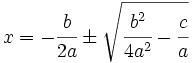
8. Se simplifica la expresión:
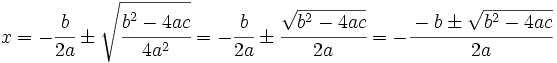
Ejemplo: Resolución de la ecuación de segundo grado
- Ejemplos de ecuaciones de segundo grado resueltas.
Pulsa "Inicio" para ver otros ejemplos:
Discriminante de una ecuación de segundo grado
Llamamos discriminante de una ecuación de segundo grado a:
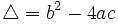
por tanto:
- Si
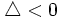 la ecuación no tiene solución.
la ecuación no tiene solución.
- Si
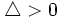 la ecuación tiene dos soluciones.
la ecuación tiene dos soluciones.
- Si
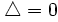 la ecuación tiene una solución (doble).
la ecuación tiene una solución (doble).
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado 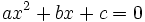 es incompleta, si ocurre uno de los siguientes casos:
es incompleta, si ocurre uno de los siguientes casos:
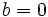 :
: 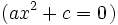
- En este caso las soluciones se obtienen despejando x:
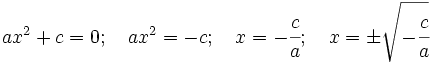
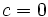 :
: 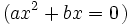
- En este caso, sacando factor común e igualando a cero cada factor:
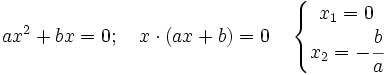
Ejemplo: Ecuaciones de segundo grado incompletas
- Ejemplos de ecuaciones de segundo grado incompletas resueltas.
Pulsa "INICIO" para ver otros ejemplos:
- Caso 1:
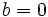 :
: 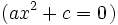
- Caso 2:
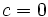 :
: