Plantilla:Dominio e imagen de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:34 20 ene 2009 Coordinador (Discusión | contribuciones) (→Dominio de definición e imagen) ← Ir a diferencia anterior |
Revisión de 17:36 20 ene 2009 Coordinador (Discusión | contribuciones) (→Dominio de definición e imagen) Ir a siguiente diferencia → |
||
| Línea 49: | Línea 49: | ||
| ::a) <math>y=x-3\;\!</math>, {{b4}}b) <math>y=\cfrac{1}{x-1}</math>, {{b4}}c) <math>y=\sqrt{x}</math> | ::a) <math>y=x-3\;\!</math>, {{b4}}b) <math>y=\cfrac{1}{x-1}</math>, {{b4}}c) <math>y=\sqrt{x}</math> | ||
| |sol= | |sol= | ||
| - | :a) Su dominio es <math>\mathbb{R}</math>, porque cualquier valor de <math>x</math> da un valor de <math>y</math> válido. | + | :a) Su dominio es <math>\mathbb{R}</math>, porque cualquier valor de <math>x\;</math> da un valor de <math>y\;</math> válido. |
| :b) Su dominio es <math>\mathbb{R}- \left \{ 1 \right \}</math>, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división. | :b) Su dominio es <math>\mathbb{R}- \left \{ 1 \right \}</math>, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división. | ||
| :c) Su dominio es <math>\mathbb{R^+}</math>, porque el radicando no puede ser negativo para poder hallar la raíz. | :c) Su dominio es <math>\mathbb{R^+}</math>, porque el radicando no puede ser negativo para poder hallar la raíz. | ||
Revisión de 17:36 20 ene 2009
Dominio de definición e imagen
Llamamos dominio de definición de una función y = f(x) al conjunto de valores de la variable independiente x para los cuales existe el valor de y. Lo representaremos por Df .
La imagen o recorrido de una función es el conjunto de valores que toma la variable dependiente y. Lo representaremos por Imf .
|
Actividad Interactiva: Dominio e imagen
1. Determina el dominio y la imagen de las siguientes funciones.
Actividad: Observa la escena y mueve el punto P para ver los valores que recorren las variables: a) Suponiendo que la gráfica se comporta de forma análoga a lo largo de todo el eje X,¿Cuál es su dominio y su imagen? Observa esta otra escena y procedede como antes: b) ¿Cuál es su dominio y su imagen? Haz lo mismo con esta tercera escena: |
Ejemplo: Dominio de una función
- Halla el dominio de las funciones:
- a)
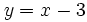 , b)
, b) 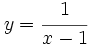 , c)
, c) 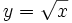
- a)
Solución:
- a) Su dominio es
 , porque cualquier valor de
, porque cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
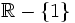 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
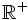 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
Ejercicios
|
Ejercicios: Dominio e imagen |

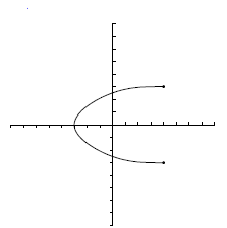
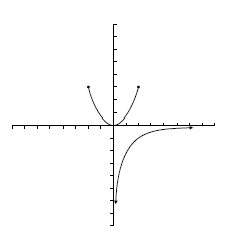
![D=[-3.5, 4]\;\!](/wikipedia/images/math/6/f/4/6f4030ef099e99944025cbb34e75c6ae.png) .
. ![Im=[-4, 3]\;\!](/wikipedia/images/math/4/9/c/49cf9064f7a20c06eb8cb9c71af85beb.png) .
.

