Transformaciones elementales de funciones (1ºBach)
De Wikipedia
| Revisión de 17:36 23 ene 2009 Coordinador (Discusión | contribuciones) (→Dilatación y contracción) ← Ir a diferencia anterior |
Revisión de 17:39 23 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 2: | Línea 2: | ||
| |ir= | |ir= | ||
| |ampliar= | |ampliar= | ||
| - | |repasar=[http://www.maralboran.org/web_ma/algebraconpapas/index.htm Test de Álgebra] | + | |repasar= |
| |enlaces= | |enlaces= | ||
| }} | }} | ||
Revisión de 17:39 23 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Traslación vertical
Sea  una función y
una función y 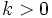 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 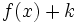 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola  unidades hacia arriba y la de
unidades hacia arriba y la de 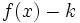 desplazándola
desplazándola  unidades hacia abajo.
unidades hacia abajo.
|
Actividad Interactiva: Traslación vertical de una función
Actividad 1. Representación gráfica de una función
 cualquiera y de su transformada cualquiera y de su transformada 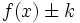 . .Actividad: En esta escena tienes la gráfica de la función  (en verde) y la de (en verde) y la de 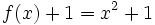 (en amarillo). (en amarillo).
Prueba a cambiar el valor de
Prueba a cambiar también la función |
Simetría respecto del eje X
Las gráficas de las funciones  y su opuesta,
y su opuesta, 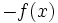 , son simétricas respecto del eje de abscisas.
, son simétricas respecto del eje de abscisas.
|
Actividad Interactiva: Función simétrica respecto del eje X
Actividad 1. Representación gráfica de una función
 cualquiera y de su simétrica cualquiera y de su simétrica 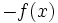 . .Actividad: En esta escena tienes la gráfica de la función 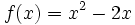 (en verde) y la de su simétrica (en verde) y la de su simétrica 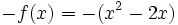 (en amarillo). (en amarillo).
Prueba a cambiar la función |
Dilatación y contracción
- Si
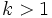 , la gráfica de la función
, la gráfica de la función 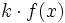 es una dilatación o estiramiento vertical de la gráfica de
es una dilatación o estiramiento vertical de la gráfica de  .
.
- Si
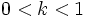 , la gráfica de la función
, la gráfica de la función 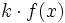 es una contracción o achatamiento vertical de la gráfica de
es una contracción o achatamiento vertical de la gráfica de  .
.
- Si
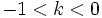 , la gráfica de la función
, la gráfica de la función 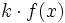 es la combinacion de una contracción y una simetría respecto del eje X.
es la combinacion de una contracción y una simetría respecto del eje X.
- Si
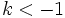 , la gráfica de la función
, la gráfica de la función 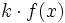 es la combinacion de una dilatación y una simetría respecto del eje X.
es la combinacion de una dilatación y una simetría respecto del eje X.
|
Actividad Interactiva: Dilatación y contracción de una función
Actividad 1. Representación gráfica de una función
 cualquiera y de su transformada cualquiera y de su transformada 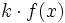 . .Actividad: En esta escena tienes la gráfica de la función 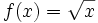 (en verde) y la de su dilatada (en verde) y la de su dilatada 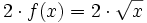 (en amarillo). (en amarillo).
Prueba a cambiar el valor de
|
Traslación horizontal
Sea  una función y
una función y 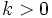 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 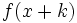 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola  unidades hacia la izquierda y la de
unidades hacia la izquierda y la de 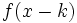 desplazándola
desplazándola  unidades hacia la derecha.
unidades hacia la derecha.
|
Actividad Interactiva: Traslación horizontal de una función
Actividad 1. Representación gráfica de una función
 cualquiera y de su transformada cualquiera y de su transformada 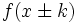 . .Actividad: En esta escena tienes la gráfica de la función 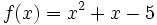 (en verde) y la de (en verde) y la de 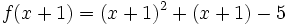 (en amarillo). (en amarillo).
Prueba a cambiar el valor de
Prueba a cambiar también la función |
Simetría respecto del eje Y
Las gráficas de las funciones  y su opuesta,
y su opuesta, 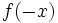 , son simétricas respecto del eje de ordenadas.
, son simétricas respecto del eje de ordenadas.
|
Actividad Interactiva: Función simétrica respecto del eje Y
Actividad 1. Representación gráfica de una función
 cualquiera y de su simétrica cualquiera y de su simétrica 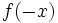 . .Actividad: En esta escena tienes la gráfica de la función 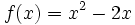 (en verde) y la de su simétrica (en verde) y la de su simétrica 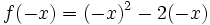 (en amarillo). (en amarillo).
Prueba a cambiar la función |
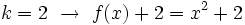 .
.
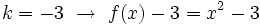
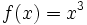 .
.
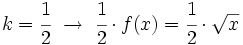 . Obtendrás una contracción de
. Obtendrás una contracción de 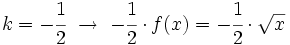 . Obtendrás una contracción de
. Obtendrás una contracción de 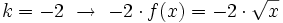 . Obtendrás una dilatación de
. Obtendrás una dilatación de 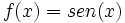 .
.
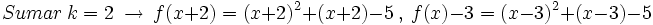 .
.
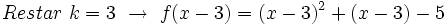 .
.
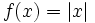 . (La función valor absoluto debes escribirla abs(x)).
. (La función valor absoluto debes escribirla abs(x)).
 .
.

