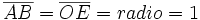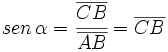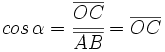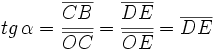Razones trigonométricas de ángulos cualesquiera (1ºBach)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 18:54 20 feb 2009

Menú:

Enlaces internos	Para repasar o ampliar	Enlaces externos
Indice Descartes Manual Casio		WIRIS Geogebra Calculadoras

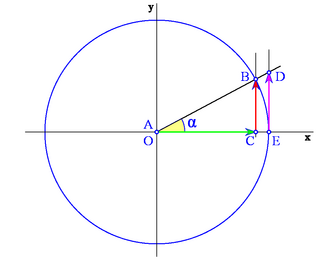
Circunferencia goniométrica

Vamos a establecer un sistema de referencia para el estudio de los ángulos de cualquier cuadrante.

Consideremos una circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con su centro en el origen de coordenadas O. Sobre ella situaremos nuestro triángulo rectángulo ABC, haciendo coincidir su vértice A con O, el cateto contiguo al ángulo $\alpha \;$ lo situaremos en el eje X positivo y la hipotenusa coincidiendo con el radio, tal y como se muestra en la figura. A esta circunferencia la llamaremos circunferencia goniométrica.

Teniendo en cuenta que $\overline{AB} = \overline{OE}= radio = 1$ y la semejanza de los triángulos ABC y ADE, las razones trigonométricas del águlo $\alpha \;$ se expresan de la siguiente manera:

$sen \, \alpha = \cfrac{\overline{CB}}{\overline{AB}}=\overline{CB}$

$cos \, \alpha = \cfrac{\overline{OC}}{\overline{AB}}=\overline{OC}$

$tg \, \alpha = \cfrac {\overline{CB}}{\overline{OC}}=\cfrac{\overline{DE}}{\overline{OE}}=\overline{DE}$

Por tanto, las coordenadas del punto B son 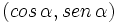$(cos \, \alpha , sen \, \alpha )$ . Y por extensión, podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:

Dado un ángulo $\alpha \,$ , se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte del segundo lado del ángulo con la circunferencia goniométrica:

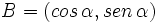
$B=(cos \, \alpha , sen \, \alpha )$

Nota: Las relaciones fundamentales de la trigonometría, ya estudiadas anteriormente, siguen siendo válidas con esta definición.

Círculo Goniométrico (12'55") Sinopsis:

Razones trigonométricas de un ángulo. Fórmula fundamental.
Circúlo goniométrico.
Interpretación geométrica de las razones trigonométricas.
Medida en grados y radianes.
Tablas de las razones trigonométricas de los ángulos principales.
Signo de las razones trigonométricas segun el cuadrante del ángulo.

Obtenido de "http://maralboran.org/wikipedia/index.php/Razones_trigonom%C3%A9tricas_de_%C3%A1ngulos_cualesquiera_%281%C2%BABach%29"

Categorías: Matemáticas | Geometría

 }}
 {{p}}
+*'''Nota:''' Las [[Razones trigonométricas de un ángulo agudo (1ºBach)#Relaciones fundamentales de la trigonometría|relaciones fundamentales de la trigonometría]], ya estudiadas anteriormente, siguen siendo válidas con esta definición.
 {{Video_enlace2
 |titulo1=Círculo Goniométrico

Razones trigonométricas de ángulos cualesquiera (1ºBach)

De Wikipedia

Revisión de 18:54 20 feb 2009

Circunferencia goniométrica

Vistas

Herramientas personales

Menú

Buscar

Herramientas