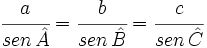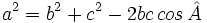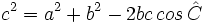Resolución de triángulos cualesquiera (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:36 1 mar 2009 Coordinador (Discusión | contribuciones) (→Teorema de los senos) ← Ir a diferencia anterior |
Revisión de 17:38 1 mar 2009 Coordinador (Discusión | contribuciones) (→Teorema de los senos) Ir a siguiente diferencia → |
||
| Línea 15: | Línea 15: | ||
| }} | }} | ||
| |demo= | |demo= | ||
| - | [[Imagen:Ley de los senos-prueba.svg|thumb|263px|right|El teorema de los senos establece que ''a/sin(A)'' es constante.]] | + | [[Imagen:terorema senos.png|263px|right|El teorema de los senos establece que ''a/sin(A)'' es constante.]] |
| Dado el triángulo ''ABC'', denotamos por ''O'' su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento ''BO'' hasta cortar la circunferencia, se obtiene un diámetro ''BP''. | Dado el triángulo ''ABC'', denotamos por ''O'' su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento ''BO'' hasta cortar la circunferencia, se obtiene un diámetro ''BP''. | ||
Revisión de 17:38 1 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Teorema de los senos
Teorema de los senos
Demostración:
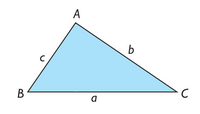
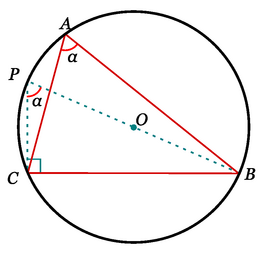
Dado el triángulo ABC, denotamos por O su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento BO hasta cortar la circunferencia, se obtiene un diámetro BP.
Ahora, el triángulo PBC es recto, puesto que BP es un diámetro, y además los ángulos A y P son iguales, porque ambos son ángulos inscritos que abarcan el mismo segmento BC. Por la definición de seno, se tiene
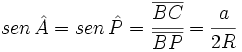
donde R es el radio de la circunferencia. Despejando 2R obtenemos:
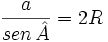
Teorema del coseno
Teorema del coseno
Demostración: