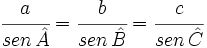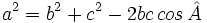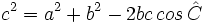Resolución de triángulos cualesquiera (1ºBach)
De Wikipedia
| Revisión de 17:44 1 mar 2009 Coordinador (Discusión | contribuciones) (→Teorema de los senos) ← Ir a diferencia anterior |
Revisión de 17:48 1 mar 2009 Coordinador (Discusión | contribuciones) (→Teorema del coseno) Ir a siguiente diferencia → |
||
| Línea 45: | Línea 45: | ||
| }} | }} | ||
| |demo= | |demo= | ||
| + | Notemos que el Teorema de Cosenos es equivalente al Teorema de Pitágoras cuando el ángulo <math>\gamma</math> es recto. Por tanto sólo es necesario considerar los casos cuando ''c'' es adyacente a dos ángulos agudos y cuando ''c'' es adyacente a un ángulo agudo y un obtuso. | ||
| + | |||
| + | '''Primer caso:''' ''c'' es adyacente a dos ángulos agudos. [[Imagen:CosenosPorPitagoras1.png|Caso 1: ''c'' es adyacente a dos ángulos agudos]] | ||
| + | |||
| + | Consideremos la figura adjunta. El teorema de Pitágoras establece que ''c² = h² + u²'' de modo que ''h² = a² - (b-u)²''. | ||
| + | Combinando ambas ecuaciones y luego simplificando obtenemos ''c² = u² + a² - b² + 2bu - u²'', es decir: | ||
| + | {{Ecuación|<math>c^2 = a^2 - b^2 + 2bu\,</math>|3=left}} | ||
| + | |||
| + | Por la definición de coseno, se tiene cos(γ) = (b-u)/a, por tanto | ||
| + | {{Ecuación|<math> u = b- a \,\cos\gamma\,</math>|3=left}} | ||
| + | Sustituimos el valor de u en la expresión para ''c²'' y simplificamos: ''c² = a²-b² +2b ''(''b-a ''cos(γ)), concluyendo | ||
| + | {{Ecuación|<math> c^2 = a^2 +b^2 -2ab\, \cos \gamma</math>|3=left}} | ||
| + | y terminando con esto la prueba del primer caso. | ||
| + | |||
| + | |||
| + | '''Segundo caso:''' ''c'' es adyacente a un ángulo obtuso. [[Imagen:CosenosPorPitagoras2.png|Caso 2: ''c'' es adyacente a un ángulo obtuso]] | ||
| + | |||
| + | Consideremos la figura adjunta. El teorema de Pitágoras establece nuevavamente ''c² = h² + u²'' pero en este caso ''h² = a² - (b+u)²''. Combinando ambas ecuaciones obtenemos <math> c^2 = u^2 + a^2 - b^2 - 2bu - u^2 </math> y de este modo: | ||
| + | {{Ecuación|<math>c^2 = a^2 -b^2 -2bu\,</math>.|3=left}} | ||
| + | |||
| + | De la definición de coseno, se tiene cos(γ) = (b+u)/a y por tanto | ||
| + | {{Ecuación|<math> u = a\, \cos\gamma -b\,</math>.|3=left}} | ||
| + | Sustituimos en la expresión para ''c²'' y simplificamos ''c² = a²-b² -2b''(''a'' cos(γ)-''b''), concluyendo nuevamente | ||
| + | {{Ecuación|<math> c^2 = a^2 +b^2 -2ab\, \cos \gamma\,</math>.|3=left}} | ||
| + | Esto concluye la demostración. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 17:48 1 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Teorema de los senos
Teorema de los senos
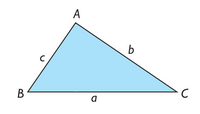
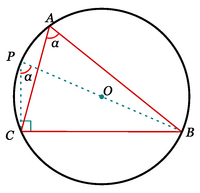
Dado el triángulo ABC, denotamos por O su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento 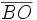 hasta cortar la circunferencia, se obtiene un diámetro
hasta cortar la circunferencia, se obtiene un diámetro 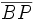 .
.
Ahora, el triángulo PBC es recto, puesto que 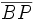 es un diámetro, y además los ángulos
es un diámetro, y además los ángulos 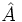 y
y 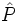 son iguales, porque ambos son ángulos inscritos que abarcan el mismo segmento
son iguales, porque ambos son ángulos inscritos que abarcan el mismo segmento 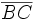 . Por la definición de seno, se tiene
. Por la definición de seno, se tiene
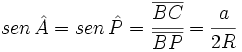
donde R es el radio de la circunferencia. Despejando 2R obtenemos:
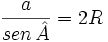
Teorema del coseno
Teorema del coseno
Notemos que el Teorema de Cosenos es equivalente al Teorema de Pitágoras cuando el ángulo γ es recto. Por tanto sólo es necesario considerar los casos cuando c es adyacente a dos ángulos agudos y cuando c es adyacente a un ángulo agudo y un obtuso.
Primer caso: c es adyacente a dos ángulos agudos. 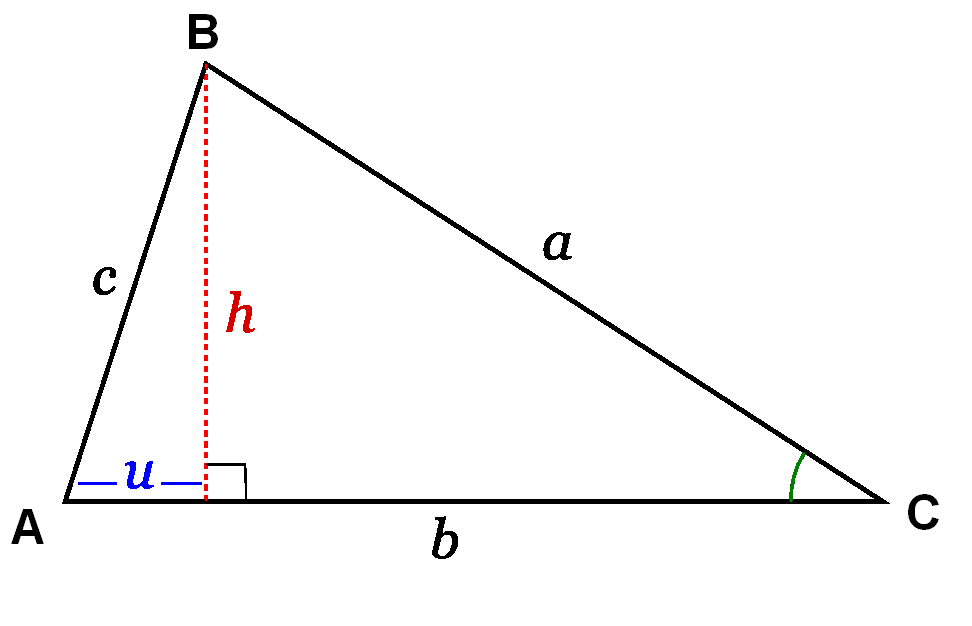
Consideremos la figura adjunta. El teorema de Pitágoras establece que c² = h² + u² de modo que h² = a² - (b-u)². Combinando ambas ecuaciones y luego simplificando obtenemos c² = u² + a² - b² + 2bu - u², es decir:
| {{{fórmula}}} | {{{ref}}} |
Por la definición de coseno, se tiene cos(γ) = (b-u)/a, por tanto
| {{{fórmula}}} | {{{ref}}} |
Sustituimos el valor de u en la expresión para c² y simplificamos: c² = a²-b² +2b (b-a cos(γ)), concluyendo
| {{{fórmula}}} | {{{ref}}} |
y terminando con esto la prueba del primer caso.
Segundo caso: c es adyacente a un ángulo obtuso. 
Consideremos la figura adjunta. El teorema de Pitágoras establece nuevavamente c² = h² + u² pero en este caso h² = a² - (b+u)². Combinando ambas ecuaciones obtenemos c2 = u2 + a2 − b2 − 2bu − u2 y de este modo:
| {{{fórmula}}} | {{{ref}}} |
De la definición de coseno, se tiene cos(γ) = (b+u)/a y por tanto
| {{{fórmula}}} | {{{ref}}} |
Sustituimos en la expresión para c² y simplificamos c² = a²-b² -2b(a cos(γ)-b), concluyendo nuevamente
| {{{fórmula}}} | {{{ref}}} |