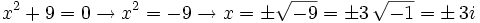Números complejos: Definición (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:33 4 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:42 4 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 13: | Línea 13: | ||
| que no tienen solución en el conjunto de los números reales | que no tienen solución en el conjunto de los números reales | ||
| - | <center><math>x^2 +9 = 0 \rightarrow x^2=-9 \rightarrow x=\sqrt{-9}</math></center> (no existe en <math>\mathbb{R}</math>) | + | <center><math>x^2 +9 = 0 \rightarrow x^2=-9 \rightarrow x=\pm \sqrt{-9}</math></center> (no existe en <math>\mathbb{R}</math>) |
| Vamos a definir un ´uevo conjunto que amplie al conjunto de los números reales y en el cual estas ecuaciones si tengan solución. Para ello vamos a dar sentido a las raíces de números negativos. | Vamos a definir un ´uevo conjunto que amplie al conjunto de los números reales y en el cual estas ecuaciones si tengan solución. Para ello vamos a dar sentido a las raíces de números negativos. | ||
| Línea 22: | Línea 22: | ||
| <center><math>i=\sqrt{-1}</math></center>}} | <center><math>i=\sqrt{-1}</math></center>}} | ||
| {{p}} | {{p}} | ||
| + | Con esta definición, la ecuación anterior ahora si tiene solución "imaginaria": | ||
| + | |||
| + | <center><math>x^2 +9 = 0 \rightarrow x^2=-9 \rightarrow x=\pm \sqrt{-9}=\pm 3 \, \sqrt{-1}=\pm \, 3i</math></center> | ||
| ==Números complejos en forma binómica== | ==Números complejos en forma binómica== | ||
Revisión de 18:42 4 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Necesidad de ampliación del campo numérico
Hay ecuaciones como
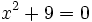
que no tienen solución en el conjunto de los números reales
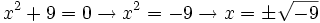
 )
)
Vamos a definir un ´uevo conjunto que amplie al conjunto de los números reales y en el cual estas ecuaciones si tengan solución. Para ello vamos a dar sentido a las raíces de números negativos.
Unidad imaginaria
Se denomina unidad imaginaria a 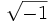 . Se designa por la letra
. Se designa por la letra 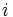
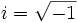
Con esta definición, la ecuación anterior ahora si tiene solución "imaginaria":